1. 서 론
2. 이론적 배경
2.1 공극탄성 이론
2.2 무자켓(Unjacketed) 실험
3. 실험 프로그램
3.1 기본 물성
3.2 실험장비
3.3 실험수행
4. 실험결과
5. 결 론
1. 서 론
지속가능한 에너지 자원개발, 기후변화 대응 등과 같은 전 지구적 문제를 해결하고자 해외 각국은 고준위방사성폐기물 심층처분, 이산화탄소 지중저장, 심부지열개발 등과 같이 심지층 환경을 활용하거나 개발하는 프로젝트를 국가적인 차원에서 수행하고 있다. 안전하고 성공적인 심지층 환경 프로젝트의 수행을 위해서는 심부 암반 특성화 기술의 확보가 반드시 필요하다(Blanco et al., 2016, Yoon et al., 2019, Rutqvist, 2020, Cheon et al., 2022, Yoon et al., 2022, Youn et al., 2022). 그중에서도 심지층 환경은 고온 고압 환경에서 발생하는 암반의 열-수리-역학적 연계 특성이 복합적으로 작용하기 때문에 수치해석 모델을 통한 특성 분석 기술개발이 대두되고 있다(Cho et al., 2012, Rutqvist et al., 2009, Yoon et al., 2018, Lee et al., 2019, Jeong et al., 2022, Park and Park, 2022).
심지층 환경에서 투수성이 양호한 다공성 매질(Porous media)이 지하수로 포화된 경우 암반의 역학적 변형과 공극수압이 상호작용을 하게 되며 이는 가장 기본적인 암반의 수리-역학적 모델이라고 볼 수 있다. 암석 체적계수는 실험 조건 및 방법에 따라서 입자 체적계수(Grain bulk modulus), 배수 체적계수(Drained bulk modulus), 비배수 체적계수(Undrained bulk modulus)로 나눌 수 있다. 세 가지 체적계수 모두 수리-역학적 관계를 나타내는 인자로 중요한 의미가 있으나, 특히 암석 입자 체적계수는 암석 고유의 특성에 해당되기 때문에 가장 기본이 되는 인자이며(Hart and Wang, 1995, Hart and Wang, 2010), 공극 내 수리-역학적 관계의 특성을 파악할 수 있는 중요한 인자 중에 하나이다(Belmokhtar et al., 2017).
암석 입자 체적계수는 공극의 수리적 압력에 의해 변화되는 암석의 역학적 체적 변화를 나타내는 인자로써, 공극 수압의 변화에 따른 체적 변화의 비율로 정의된다. 암석 입자 체적계수의 분석을 통해 심지층 환경에서 대상 암반의 구속압력의 변화가 체적 변화에 미치는 영향을 파악할 수 있다. 암석 입자 체적계수는 암반의 열-수리-역학적 복합거동 예측을 위한 수치해석 자료의 지배방정식에 필수적인 입력 값으로 사용되며, 해당 물성의 신뢰성 있는 입력값 설정은 고준위방사성폐기물 심층처분시스템의 안정성 평가 결과와 같은 심지층 환경 개발 프로젝트의 설계에 큰 영향을 미칠 수 있다.
기존 연구에서 암석 입자 체적계수는 암석을 구성하고 있는 광물의 구성비를 구하고, 광물별 체적계수 값을 이용하여 간단하고 효율적으로 추정하는 방법을 사용했으나(Qin et al., 2022), 이는 입자의 고결화(Cementation)와 암체 구조(Matrix)와 같은 구성 광물들의 경계에서 발생하는 상호 작용 및 기하학적 요인을 정확히 고려하지 못하기 때문에 과소 혹은 과대평가되는 경향이 있다. 이에 따라 암석 입자 체적계수를 구하는 방법으로는 직접적인 실험법을 통한 결과 분석이 가장 신뢰성 있고 정확한 것으로 알려져 있다(Qin et al., 2022). 그럼에도 불구하고 입자 체적계수에 대해 직접적인 측정을 위한 표준화된 시험 방법이 미국재료시험협회(American Society for Testing and Materials, ASTM)나 국제암반공학회(International Society for Rock Mechanics, ISRM)의 표준시험법에 따로 제시되어있지 않기 때문에 이를 실험적으로 도출하고 신뢰성을 확보하는 연구가 필요한 실정이다.
본 연구에서는 암반 수리-역학적 관계의 기본모델 입력인자인 암석 입자 체적계수에 대하여 직접적인 측정 실험법을 제시하고, 실험을 수행함으로써 암석 입자 체적계수를 도출하였다. 또한, 서로 다른 기하학적 특성을 가진 암석에 대하여 입자 체적계수를 구하고 비교함으로써 입자 체적계수에 영향을 미치는 요인에 대해 살펴보았다.
2. 이론적 배경
2.1 공극탄성 이론
심부 암반의 수리-역학적 관계에 있어 가장 근간이 되는 이론적 배경은 다공성 매질의 탄성 거동을 다루고 있는 공극탄성(Poroelasticity) 이론이다. 이는 선형 다공성 매질 내에서 유체 흐름과 고체 변형 사이의 상호 작용을 나타내는 이론으로, 포화 상태 및 탄성 구간 내에서의 암반의 역학적인 변형 특성을 나타낸다. 매질 내 유체의 흐름은 매질의 고체에서 변형을 일으킬 수 있으며, 마찬가지로 고체의 변형은 유체의 흐름에 영향을 미치게 된다. 공극탄성 이론에 의한 공극압력과 응력과의 관계는 식 (1)과 같이 나타낼 수 있다(Biot, 1956).
여기서, σʹ는 유효응력, σ는 전체 응력, P는 공극에 작용하는 유체의 압력, α는 Biot 계수로 알려진 공극탄성 이론에 사용되는 상수이다.
식 (1)에 따라, 심부 환경의 수리적 흐름에 의한 암석 입자 내 공극압력이 역학적 변형에 영향을 미치게 됨을 알 수 있다. 한편, 공극압력이 역학적 변형에 미치는 영향은 Biot 계수에 비례하게 되는데, Biot 계수는 식 (2)와 같이 나타낼 수 있다(Biot, 1941).
여기서, Kd는 대상 암석의 전체 배수 체적계수, Ks는 암석 입자 체적계수를 의미한다. 암석을 입자 단위로 보면 암석의 체적 변화는 입자만의 체적 변화와 공극에서의 체적 변화의 합으로 볼 수 있다. 따라서 Fig. 1과 같이 암석 전체의 체적 변화는 입자만의 체적 변화보다 항상 큰 값을 갖게 되며 체적계수와 체적 변화는 체적변형 계수 정의에 따라 반비례 관계에 있으므로 체적계수 값은 Kd > Ks가 된다. 따라서 Biot 계수는 1이하의 값을 갖게 된다.
식 (2)와 같이 입자 체적계수는 Biot 계수 값의 크기를 결정함으로써 암반의 수리-역학적 관계에까지 영향을 미치게 된다. 뿐만 아니라 체적계수 값은 심지층 활용을 위한 암반의 열-수리-역학적 연계 특성 수치해석 모델의 입력값으로도 사용되기 때문에(Park et al., 2019) 이를 정확하게 산정하는 것은 매우 중요하다.
2.2 무자켓(Unjacketed) 실험
체적계수를 포함한 공극탄성 이론을 구성하고 있는 기본 인자들의 값을 구하기 위해서는 정수압 상태의 조건이 구현되기 때문에 구속압의 제어가 가능한 삼축 압축 조건에서의 실험이 수행되어야 한다. 공극탄성 이론의 인자를 구하기 위한 삼축 실험은 실험 조건에 따라 무자켓, 배수, 비배수 실험으로 나눌 수 있다(Lau and Chandler, 2004).
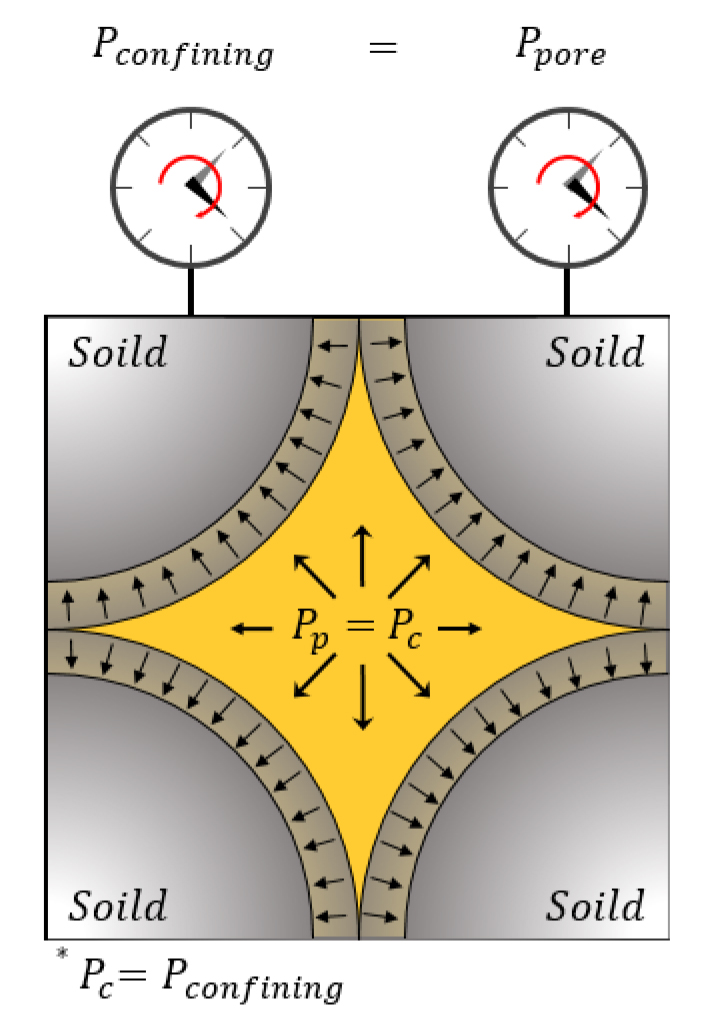
이 중, 입자 자체의 체적계수를 측정하기 위해서는 무자켓(Unjacketed) 실험이 수행되어야 한다. 무자켓 실험은 시료 외부에 멤브레인(membrane) 또는 시료 표면을 감싸는 자켓(jacket) 없이 시료에 직접적으로 구속 유체를 접촉시켜 구속압을 가해주는 실험이다. 시료 외부에 멤브레인이 없으면 구속 유체가 무결암(Intact rock) 시료의 공극 내부로 침투하게 되며, 그에 따라 시료 외부의 구속압과 시료 내부의 공극압력이 평형 상태에 도달하여 두 압력이 같아지게 된다. 즉, 유효응력(Terzaghi effective stress)이 0인 상태인 것이다(Makhnenko and Labuz, 2016). 이와 같은 상태에서는 Fig. 2와 같이 구속압력과 공극압력이 동일하게 입자에게 가해져 입자에서만의 체적 변화가 발생하게 된다.
따라서 무자켓 실험의 조건에서는 순수한 입자만의 체적이 변화하게 되며, 이 때의 구속압(MPa)과 체적변형률(-)간의 관계에 의해 식 (3)과 같이 시료의 입자 체적계수가 도출된다(Makhnenko and Labuz, 2016).
3. 실험 프로그램
본 연구에서는 무자켓 실험을 위하여 균질한 사암 시료를 대상으로 실험을 진행하였다. 실험에 사용된 사암 시료는 Kocurek industries의 Berea 및 Idaho 사암이며, 체적변형률의 정확한 측정을 위하여 NX 코어(직경 : 54 mm, 길이 : 100 mm)의 원기둥 형태로 시료를 가공하였다. 두 사암 시료 모두 암석이 균질하며 공극률 값이 각각 18 – 21%, 29 – 30%를 보여(Table 1) 구속 유체의 침투가 용이해야 하는 무자켓 실험에 적합하였다. 특히, Berea 사암의 경우 입자 체적계수를 포함한 공극탄성 이론 기본특성 인자에 대한 문헌 값이 일부 사전연구들(Makhnenko and Labuz, 2013)에 제시되어있어, 실험 결과의 비교 및 고찰이 가능하였다. 입자 체적계수를 구하기 위한 무자켓 실험의 경우, ASTM이나 ISRM에서 제시된 표준화된 시험방법이 존재하지 않기 때문에 기존 문헌과의 데이터 비교는 결과값의 고찰에 있어 매우 유용하게 활용될 수 있다.
3.1 기본 물성
무자켓 실험의 수행에 앞서, 대상 시료들의 일축압축강도, 탄성계수, 공극률에 대한 기본 물성 시험을 수행하였다.
사암 시료의 일축압축강도 측정을 위하여 MTS사의 160 ton급 암석시험용 압축기를 사용하였다. 본 장비는 유압을 시험조건에 맞게 조절하는 자동서보장치(Automatic servo control system)에 의해 모든 시험과정이 조절되는 폐쇄유압형(Closed loop type) 장비이다. 일축압축강도 시험은 ASTM D2938에 따라 실시하였으며, 시험편의 축 방향으로 압축응력을 가한 후 파괴될 때의 최대 하중을 측정하였다(ASTM, 1986). 일축압축응력에 대한 시료의 변형 특성을 분석하기 위하여 축 방향으로 다이얼게이지 형태의 변위변환기(Dial gage type displacement transducer)를 사용하고, 시료 원주 방향으로 변형 특성을 분석하기 위하여 MTS사의 원주방향 신장계(Circumferential extensometer)를 사용하여 각각의 변형률을 측정하였다. 시험 횟수는 한국암반공학회에서 제시한 ‘암석의 일축압축강도 표준시험법’에 따라 3개의 시험편에 대한 시험을 실시하였다(KSRM, 2005).
한편 암석의 공극률은 한국암반공학회에서 제시한 표준암석시험법인 ‘암석의 공극률 및 밀도 측정 표준시험법’을 참고하여 측정하였다(KSRM, 2006). 본 시험 방법은 서로 연결된 공극의 부피인 유효 공극률(effective porosity)을 측정하는 시험방법이며, 암석시료를(105 ± 3)°C에서 24시간 이상 건조하고 암석 시험편의 무게(Wdry)를 측정한 다음 800 Pa이하의 진공상태에서 시험편을 수침시켜 포화 무게(Wsat)를 측정하여 암석의 공극률을 측정하는 방법이다.
두 종류의 사암에서 구한 기본 물성의 평균값 및 표준편차는 Table 1과 같다.
Table 1.
Mechanical properties of sandstone
| Effective Porosity (%) | Uniaxial Compression Strength (MPa) | Elastic Modulus (GPa) | |
| Berea sandstone | 18 – 21 | 41.33 ± 3.79 | 9.1 ± 0.9 |
| Idaho sandstone | 29 – 30 | 20.33 ± 0.58 | 7.35 ± 0.54 |
일축압축강도와 탄성계수는 Berea 사암이 Idaho 사암보다 더 높게 나타났는데, 이는 Idaho 사암과 Berea 사암 간 공극률 차이로 인한 것으로 판단된다(Kahraman et al., 2005).
3.2 실험장비
본 연구에서 암석 시료의 입자 체적계수 측정에 사용된 장비는 MTS 815 System 이다. Fig. 3과 같이 최대 구속압 및 공극수압이 138 MPa 인 2개의 증압(intensifier) 펌프와 1개의 460 ton 용량의 하중기, 컨트롤러로 구성되어있다.
삼축조건의 구현을 위하여 시료 외부에 MTS사의 636.60 Triaxial cell을 설치하였다. 셀 내부에서는 구속압 제어를 위한 유압유를 이용하여 가압조건을 구현할 수 있도록 설정하였다. 유압유로는 미국 Guardsman사의 7USP White Oil을 사용함으로써 센서와 컨트롤러간 전기적인 신호의 교란 및 실험오차 발생 가능성을 최소화하였다.
무자켓 실험 시 시료의 체적변형률을 정밀하게 측정하기 위하여 축 및 원주 방향 신장계를 Fig. 4와 같이 설치하였다.
축방향 및 원주방향 신축계 값을 이용하여 식 (4)와 같이 체적변형률을 측정할 수 있다(Lau and Chandler, 2004).
여기서, εa는 축방향 변형률, εc는 원주방향 변형률을 나타낸다.
원주방향 신장계에서 실제로 계측되는 값은 원주의 변화시 발생하는 현의 길이의 변화로써, 식 (5)와 같이 추가적인 계산을 통해 원주 변형률의 측정이 가능하다(MTS, 2000).
여기서, △l은 신장계에서 읽어오는 현의 길이 변화이며, θi는 체인의 시작과 끝이 벌어진 초기 각도이다. △C는 원통방향 길이 변화량이다. 실험을 통해 얻어진 △C 값을 원기둥 시료의 원주로 나누면 원주방향 변형률(εc)을 계산할 수 있다.
3.3 실험수행
무자켓 실험수행을 위하여 멤브레인 설치없이 시료 표면에 축/원주방향 신장계를 설치하였다. 각 신장계가 장착된 시료는 하부 엔드캡(end cap) 아래에 있는 오링(O-ring)의 체결 상태를 확인 후 MTS 유압하중기의 시료 거치판의 상부에 올려 볼트를 체결하였다. 이후 로드셀과 신장계를 MTS 컨트롤러에 연결한 후 Platen Assembly 상승에 따른 센터 핀(center pin) 체결 및 시료와 구면좌를 밀착시키며 실험을 위한 초기 상태를 설정하였다(Fig. 5(a)).
초기 상태 설정 이후 삼축셀을 하강시키고 Bell이 완전히 닫히게 되면 볼트를 체결하여 벨 내부의 유체에 누수가 발생하지 않도록 하였다. 그 후 구속압 증압기를 조절하여 셀 내부에 구속압 유압유를 주입하고 주입이 완료되면 MTS 컨트롤러를 이용해서 무자켓 실험을 수행하였다(Fig. 5(b)).
실험 중에는 컨트롤러 운영 소프트웨어인 MTS 793의 다목적 시험 프로그램인 MPT(MultiPurpose Testware)를 이용하여 본 실험의 목적에 맞는 실험 조건을 구현하였다. 실험에서 공극 내에 구속 유체가 침투할 수 있도록 10 MPa의 구속압력으로 20분간 대기한 후 실험을 수행하였다. 이 때 구속압 증압기의 펌프 변위의 변화가 추가적으로 발생하지 않음을 확인함으로써 시료 내부에 공극압이 모두 형성되었음을 판단하였다. 가압조건은 10 – 50 MPa까지 5 MPa 간격으로 설정하였다. 최초 구속압력 조건과 마찬가지로 단계별 가압조건에서 압력값 도달 이후 펌프 변위의 변화가 발생하지 않음을 확인 후 다음 단계로 가압하였다. 가압을 위한 하중 재하속도는 2.5 MPa/min으로 가했으며, 가압조건 및 하중 재하속도는 ISRM 표준시험법을 참조하여 설정하였다(ISRM, 2016). 무자켓 실험은 각 시료별로 총 4회가 반복 수행되었다.
4. 실험결과
무자켓 실험을 통해 획득한 체적변형률-구속압 관계 및 체적계수는 Fig. 6과 같다. 측정된 체적변형률의 값은 (+) 부호가 압축 방향을 의미하는 것으로, 외부 구속압력이 증가함에 따라 증가된 체적변형률의 값만큼 시료의 전체 체적은 감소하였음을 나타낸다. 실험 결과 Berea와 Idaho 사암 모두 구속압력과 체적변형률 사이에 선형적인 관계를 보였으며, 그에 따라 체적변형률은 실험 구간인 50 MPa까지 일정하게 증가하였다. 그래프의 기울기는 식 (3)의 체적계수 값에 해당되며, 이를 통해 실험 시 적용된 구속압 구간 내에서는 구속압에 따른 입자 체적계수의 변화가 크지 않음을 확인하였다. 실험을 통해 도출한 입자 체적계수의 값은 Berea 사암이 28.9 GPa 였던 반면에, Idaho 사암은 32.8 GPa로 나타났다. 시료별 비교결과 Berea 사암의 체적변형률이 0.00154로 Idaho 사암의 체적변형률인 0.00137 보다 약 11.1% 더 큰 체적변화를 보였다. Fig. 7은 시료별 체적변형률의 측정 평균값과 그에 따른 표준편차를 나타내고 있다.
본 실험으로부터 도출된 입자 체적계수의 신뢰성을 살펴보기 위하여 Berea 사암의 입자 체적계수에 대하여 선행연구(Makhnenko and Labuz, 2016)에서 구해진 입자 체적계수의 값(29.1-29.4 GPa)과 비교하였으며, 그 결과 두 값의 차이는 1.2% 내외로 유사한 수준을 보였다. 또한 구성 광물의 체적계수를 통해 환산한 입자 체적계수와도 비교를 수행하였다(Table 2). Makhnenko and Labuz(2016)에서 대상 시료인 Berea 사암은 석영 90%, 장석 7%, 방해석 1%, 산화 철 0.5%, 점토 광물 1%, 그 외 기타 광물 0.5%로 구성되어있으며, 입자의 크기는 0.02 mm 이다. 이를 각 광물별 고유의 체적계수 값을 참고하여 구성비별 체적계수를 전체로 환산했을 때 Berea 사암의 입자 체적계수는 37.56 GPa로 나타났다(Mavko et al., 2020).
Table 2.
Grain bulk modulus of sandstone (Qin et al., 2022, Deer et al., 1997)
실험 결과값은 광물 구성비를 이용한 추정 값보다 약 76.9%의 수준으로 더 낮게 나타났다. 이를 통해 광물 구성비로 시료의 체적계수를 도출했을 때 실제 체적계수 값을 과대 예측하는 것을 알 수 있으며, 실제 구속압에 의해 발생하는 암석 입자들의 체적 변화는 이론값보다 더 크게 나타난다는 것을 의미한다. 이와 같은 차이가 발생하는 이유는 연결되지 않고 고립돼 있는 공극(non-connected pore space)과 반응성이 높은 점토 광물의 존재 때문인 것으로 판단된다(Tarokh et al., 2018, Hart and Wang, 2010). 특히, 고립된 공극의 존재는 순수 구성 광물들만의 체적변화에 더해 추가적인 시료의 체적변화를 발생시킴으로써 실제 암석 체적계수는 이론 추정값보다 더 낮은 값을 보이게 된다.
한편 평균 0.2 mm의 입자 크기에 석영 55%, 장석 37%, 운모 5%, 점토 광물 3%로 구성되어 있는 Idaho 사암(Haimson and Lee, 2004, Ishutov et al., 2015)의 경우 입자 체적계수 값이 제시된 선행연구가 존재하지 않기 때문에 직접적인 비교는 불가능하였다. 광물 구성비와 각각의 체적계수를 이용하여 이론적으로 계산하였을 때 Idaho 사암의 입자 체적계수는 39.77 GPa가 나왔다. 이는 실험을 통해 구한 입자 제적계수보다 17.6% 더 큰 값으로 앞선 Berea 사암의 결과와 동일하게 과대 예측하는 것으로 볼 수 있다.
두 사암은 입자 체적계수에 차이가 발생하였으며 Idaho의 값이 Berea의 값보다 더 크게 나타났다. 두 사암에서 발생한 체적변형률 특성 및 입자 체적계수의 차이는 기본적으로 광물의 구성비의 차이로부터 기인하였을 것으로 판단된다. 구체적으로 두 사암 내에서 구성광물간의 경계에서 발생하는 화학적 상호작용, 고립돼있는 공극의 부피가 입자 체적계수의 차이에 큰 영향을 미치는 것으로 분석하였다. Idaho 사암의 경우 Berea 사암 보다 입자크기(Grain size)가 크고 공극률이 크게 나타난다. 이론적으로 공극률은 입자크기에 영향을 받지 않고 입자구조(matrix)의 형상이나 입자 사이의 고결상태에 영향을 받는다(Cheon et al., 2021). 공극률이 큰 Idaho 사암은 Berea 사암보다 입자구조가 격자로 발달되어 입자 사이의 고결상태가 양호하며, 이에 따라 입자사이의 연결되지 않고 고립된 공극의 발달이 더 적게 생성될 것으로 판단된다. 이와 같은 영향으로 Idaho 사암에서는 적게 생성된 고립된 공극만큼 체적 변화가 작게 나타나며 그에 따라 체적계수는 더 크게 나타난다고 볼 수 있다. 또한 유효 공극률과는 상관없이 고립된 공극의 크기가 큰 Berea 사암이 Idaho 사암보다 일축압축강도와 탄성계수가 더 큼에도 불구하고 체적변화는 더 크게 발생한 것으로 판단된다.
따라서 입자 체적계수는 구성 광물 자체의 영향을 받지만 광물의 구성비 자체로 체적계수를 결정할 수는 없다. 이는 고립된 공극의 존재, 입자간 접촉에 의해 발생하는 화학적 작용 등으로 인해 실제 측정값과는 다른 결과를 보일 수 있기 때문이다. 이러한 차이가 식 (3)에 의해 Biot 계수 값의 차이를 초래할 수 있으며, 나아가 수치해석 결과값의 오차를 발생시키는 요인으로 작용할 수 있다. 따라서 해당 시료에 대해 정확한 입자 체적계수를 실험에 의해 측정하여 도출해내는 것이 필요할 것으로 판단된다.
한편 기본물성 결과와 비교한 결과 입자 체적계수 값은 일축압축강도, 탄성계수 및 공극률과는 직접적인 연관성이 없는 것으로 나타났다. 특히 본 연구에서는 암석의 수리-역학적 물성에 큰 영향을 미치는 공극률의 경우 입자 체적계수에 미치는 영향은 없었다. 이는 공극률이 입자 자체의 체적변형 특성에는 영향을 미치지 않음을 나타낸다. 단, 공극을 포함한 암석의 전체 체적계수는 시료의 공극률에 큰 영향을 받을 것으로 예상된다.
5. 결 론
암석 입자 체적계수는 연속체 수치해석의 지배방정식 필수 입력 인자이며 구속압력과 체적변형률의 관계는 암반의 열-수리-역학적 거동 수치해석 모델의 검증시 유용한 자료로 활용될 수 있음에도 이에 대한 실험적 측정 방안이 제시되지 않고 있다. 특히 암석 체적계수에 있어 직접적인 측정법이 가장 신뢰가 있음에도 불구하고 이에 대한 표준시험법이 존재하지 않기 때문에 신뢰성 있는 측정 실험법 구축 방안은 중요하다고 볼 수 있다.
본 연구에서는 삼축 압축 실험 장비와 축/원주방향 신장계를 이용하여 입자 체적변형을 측정할 수 있는 실험 조건을 구성함으로써 암석 입자 체적계수 측정을 위한 무자켓 실험 구축 방안을 수립하였으며 이를 통해 Berea 사암과 Idaho 사암의 입자 체적계수를 측정하였다. 도출된 Berea 사암의 입자 체적계수는 기존 문헌과의 비교를 통해 결과값의 신뢰성을 확인하였다. 또한 두 종류 사암의 체적 변형률 측정 결과를 비교함으로써 입자 체적계수에 영향을 미치는 요인에 대한 고찰을 수행하였다. 그 결과 광물의 구성비로 구한 입자 체적계수의 값이 실제보다 과대예측 하고 있음을 확인하였으며, 이는 암체의 입자 구조 및 암석 내부의 닫힌 공극의 영향에 의한 것으로 판단된다. 단, 이는 암석 내부의 입자구조에 대한 영향이 반영되지 않았으므로 추후 CT-image 분석을 통한 입자구조에 대한 해석이 추가되어야 할 것으로 판단된다.
본 연구에서 수행된 실험방법 및 실험결과는 향후 고준위방사성폐기물 심층처분시스템의 천연방벽 모암(host rock)의 수리-역학 기본물성을 검증하는 시험법을 수립할 때 기초 자료로 활용될 수 있을 것이다.