Introduction to Researches on the Characteristics of Gas Migration Behavior in Bentonite Buffer

Sinhang Kang; Jung-Tae Kim; Changsoo Lee; Jin-Seoup Kim

doi:10.7474/TUS.2021.31.5.333

Preview

Technical Note

Tunnel and Underground Space. 31 October 2021. 333-359
https://doi.org/10.7474/TUS.2021.31.5.333

Introduction to Researches on the Characteristics of Gas Migration Behavior in Bentonite Buffer

벤토나이트 완충재 내 기체 이동의 거동 특성 관련 연구 동향 소개

Sinhang Kang¹

Jung-Tae Kim²

Changsoo Lee²^*

Jin-Seoup Kim³

강 신항¹

김 정태²

이 창수²^*

김 진섭³

¹Post-Doctoral Researcher, Korea Atomic Energy Research Institute (KAERI)

²Senior Researcher, Korea Atomic Energy Research Institute (KAERI)

³Principal Researcher, Korea Atomic Energy Research Institute (KAERI)

¹한국원자력연구원 박사후연수자

²한국원자력연구원 선임연구원

³한국원자력연구원 책임연구원

^{*Corresponding Author}

ABSTRACT

Gases such as hydrogen and radon can be generated around the canister in high-level radioactive waste disposal systems due to several reasons including the corrosion of metal materials. When the gas generation rate exceeds the gas diffusion rate in the low-permeability bentonite buffer, the gas phase will form and accumulate in the engineered barrier system. If the gas pressure exceeds the gas entry pressure, gas can migrate into the bentonite buffer, resulting in pathway dilation flow and advective flow. Because a sudden occurrence of dilation flow can cause radionuclide leakage out of the engineered barrier of the radioactive waste disposal system, it is necessary to understand the gas migration behavior in the bentonite buffer to quantitatively evaluate the long-term safety of the engineered barrier. Experimental research investigating the characteristics of gas migration in saturated bentonite and research developing numerical models capable of simulating such behaviors are being actively conducted worldwide. In this technical note, previous gas injection experiments and the numerical models proposed to verify such behaviors are introduced, and the future challenges necessary for the investigation of gas migration are summarized.

Keywords

Gas migration

Clay material

Two-phase fluid flow

Coupled hydro-mechanical behavior

High-level radioactive waste disposal

고준위방사성폐기물 처분시스템에서는 처분용기 인근에서 용기 금속 물질의 부식 등 여러 이유로 인해 수소, 라돈 등의 기체가 발생할 수 있다. 기체 발생 속도가 투수계수가 낮은 벤토나이트 완충재 공극에서의 기체 확산 속도보다 커질 경우, 형성된 기체가 축적된다. 기체 압력이 증가하여 유입 압력에 도달하면 완충재 내부로 기체의 팽창 흐름 및 이류가 발생하게 된다. 기체의 급격한 팽창 흐름 발생 시 방사성 핵종이 완충재 외부로 유출될 가능성이 있으므로, 처분시설의 설계 과정에서 점토 기반 물질에서의 기체 유동의 영향성 및 공학적방벽의 건전성을 평가하기 위해 기체 이동 현상에 대한 거동 특성을 명확하게 규명할 필요가 있다. 전세계적으로 벤토나이트 완충재 내 기체 이동 현상 규명을 위한 실험적 연구와 이를 모사할 수 있는 전산 수치 모델 개발 연구가 활발히 진행되고 있다. 본 기술보고에서는 현재까지 수행된 기체 주입 시험 및 전산 수치모델 관련 주요연구를 소개하고 향후 기체 이동 현상 규명을 위한 연구 수행 방향에 대해 정리하였다.

키워드

기체 이동

점토 물질

2상 유체 유동

수리-역학 복합거동

고준위방사성폐기물 심층처분

MAIN

1. 서 론
2. 벤토나이트 내 기체 이동 특성 파악을 위한 실험적 연구
2.1 실내시험
2.2 현장시험
3. 전산 모사 해석 연구 동향
3.1 기체 이동 전산 모사 개요
3.2 전산 수치 해석 적용 모델
3.3 전산 모사 해석 연구 동향 소결
4. 결 언

1. 서 론

사용후핵연료(spent nuclear fuel)와 같은 고준위방사성폐기물(high-level radioactive waste)을 처분하기 위해 국내에서는 심층처분시스템(deep geological disposal system)을 고려 중이다(Lee et al., 2020d). 심층처분시스템은 공학적방벽(engineered barrier system)과 천연방벽(natural barrier system)을 포함하는 다중 방벽 시스템(multi-barrier system)으로 구성되며, 고준위방사성폐기물을 생태계로부터 장기간 안전하게 격리하고 방사성 물질 및 핵종 유출을 억제할 수 있도록 성능과 장기 건전성의 확보가 요구된다.

방사성폐기물 처분시스템 내 처분용기 인근에서는 무산소 조건에서 처분용기 금속 물질의 부식, 고준위방사성폐기물의 방사성 붕괴, 지하수의 방사성 분해 등 여러 가지 이유로 인해 수소, 라돈 등의 기체가 발생할 수 있다(Graham et al., 2012, Cuss et al., 2014a). 기체의 생산 속도가 투수계수가 낮은 벤토나이트 완충재 공극에서의 기체 확산 속도보다 클 경우, 기체가 점점 축적되어 기체 압력이 증가하게 되며, 기체 압력이 기체 유입 압력(gas entry pressure)에 도달하면 완충재 내부로 기체의 팽창 흐름(dilatant flow) 및 이류(advective flow)가 발생하게 된다(Horseman et al., 1999). 기체의 급격한 팽창 흐름 발생 시 방사성 핵종이 완충재 외부로 유출될 가능성이 있으므로, 처분시설의 설계 과정에서 점토 기반 물질에서의 기체 유동의 영향성 및 공학적방벽의 건전성을 평가하기 위해 기체 이동 현상에 대한 거동 특성을 명확하게 규명할 필요가 있다.

점토 물질의 거동을 정의할 때 기체 이동 특성을 적절하게 나타내기 위해서는 점토 기반 물질의 주요 특징을 고려할 필요가 있다. 점토 물질의 경우 입자 사이의 공간이 매우 작고, 비표면(specific surface)이 매우 크고, 물 분자와 점토 입자 표면 간 역학-화학적 상호작용이 활발하고, 투수계수와 인장 강도가 낮으며, 확연한 수리-역학적 복합 거동을 보인다는 특성이 있다(Tamayo-Mas and Harrington, 2020). 이러한 특성을 고려하여 Marschall et al.(2005)과 Cuss et al.(2014a)은 점토 물질에서의 기체 이동 과정에 대한 메커니즘을 4가지로 분류하였다: (i) 동수경사에 따른 공극수 유동에 의한 용해된 기체의 이류/확산, (ii) 공극을 통한 기체 이동(일반적인 2상 유체 유동(two-phase flow)), (iii) 기체 압력에 의한 국부 팽창 흐름, (iv) 기체 압력에 의해 발생되는 인장 절리에서의 기체 흐름.

첫 번째로, 기체 분자는 공극수에 용해되어 공극수의 유동에 따른 이류 또는 농도의 차이로 인한 확산을 통해 기체가 이동할 수 있다. 이류는 Darcy의 법칙을 따라 정해지고, 확산의 경우 Henry의 법칙과 Fick의 법칙을 따라 각각 공극수에 기체가 용해되는 정도와 기체 농도차에 의한 흐름이 정해진다. 두 번째로, 불포화 매질에서의 기체는 전통적인 2상 유체 유동 모델에 따라 흐름 특성이 결정될 수 있다. 기체의 유동은 고유 투수계수(intrinsic permeability), 상대 투수율(relative permeability: 투수계수-포화도 관계), 수분 보유 곡선(water retention curve: 모세관압-포화도 관계)을 따라 결정된다. 세 번째로, 기체 압력이 특정 임계 기준을 초과하게 되면 매질 내 우선 경로(preferential pathway)의 생성 및 통로 팽창이 발생하게 되고, 해당 통로를 따라 기체가 이동할 수 있다. 이러한 현상은 벤토나이트 완충재 등 점토 기반 물질에서 주로 나타나며(Marschall et al., 2005), 기체 압력에 의한 매질의 팽창 및 미세 균열 형성은 매질의 고유 투수계수를 증가시키고, 균열 형성에 따른 공극 크기의 증가로 인해 수분 보유 곡선이 변화하기 때문에, 이러한 팽창 흐름을 적절하게 모사하기 위해서는 수리-역학적 복합 모델(coupled hydro-mechanical model)을 적용한 해석이 필요하다. 마지막으로, 기체 압력에 의해 생성되는 거시적인 인장 절리를 따라 기체가 이동할 수 있다. 기체가 빠르게 생성 및 축적되는 조건에서 기체 압력이 증가하여 최소 주응력과 인장 강도의 합을 초과하게 되는 경우 인장 절리 및 기체 흐름이 발생하게 된다.

공학적방벽을 구성하는 벤토나이트 완충재 내부에서의 기체 이동은 복잡한 거동을 보이며, 첫 번째 및 두 번째 메커니즘 기반의 기존 해석 방법은 투수성이 매우 낮은 점토 기반 물질에서의 기체 이동 현상을 정확하게 모사하기 어렵다(Graham et al., 2012, Cuss et al., 2014a, Lee et al., 2020f, Tamayo-Mas and Harrington, 2020). 기체 압력에 의한 통로 팽창 및 인장 절리 발생의 불확실성 문제를 해결하고 점토 물질에서의 기체 이동을 정량적으로 모사할 수 있는 수학적 모델과 수치 모델 기법을 개발하기 위해 국내외에서 여러 연구 및 국제공동연구가 진행되고 있으며, 본 기술 보고에서는 점토 기반 물질인 벤토나이트에서의 기체 이동 특성과 관련된 주요 연구내용을 정리하여 소개하고자 한다.

2. 벤토나이트 내 기체 이동 특성 파악을 위한 실험적 연구

2.1 실내시험

다양한 실험 조건(구속 조건, 점토 종류, 포화 정도 등)에서의 실험을 통해 점토 물질 내 기체 이동(gas migration) 특성을 파악하기 위한 연구가 다수 수행되어왔다. 본 기술 보고에서는 포화 조건에서의 벤토나이트 또는 점토 시료를 활용하여 수행된 기체 주입 시험의 결과에 중점을 두고 공학적방벽 시스템에서의 벤토나이트 완충재 내 기체 유동 특성을 분석 및 정리하였다.

Pusch and Forsberg(1983)는 일정 체적 경계 조건을 갖는 포화 벤토나이트 시료(MX-80, 직경 50 mm 및 길이 10/20 mm)를 대상으로 질소와 수소 두 종류의 기체를 활용하여 기체 주입 실내시험을 수행하였으며, Fig. 1은 시험 장치의 개요도를 나타낸다. 기체 주입 시험을 통해 질소와 수소의 기체 수리전도도를 측정한 결과, 각각 2.6~8.0×10^-14 m/s, 1.2~1.8×10^-13 m/s의 범위를 나타냈다. 기체가 벤토나이트 내부로 침투하기 위해서는 5~11 MPa의 기체 압력이 필요하며, 기체 흐름 통로가 형성되었을 때 물과 기체의 유동은 서로 다른 메커니즘을 나타내고, 기체가 공극수를 대체하지 않고 균열이 발생된 미세한 통로를 통해 이동하여 포화도가 거의 변하지 않는다는 것을 관측하였다.

Pusch et al.(1985)은 포화된 MX-80 벤토나이트 시료를 활용하여 기체가 시료로 침투될 때의 임계 압력 개념의 가설 검증을 목표로 실험을 수행하였다. 염분을 포함하는 NAGRA 지하수로 벤토나이트 시료를 포화시켰고, 1.7~2.1 t/m³ 범위의 밀도를 갖는 8개의 시료를 대상으로 주입 기체 압력을 연속적으로 증가시키면서 기체 흐름을 측정함으로써 미세 구조적 관점에서의 기체 침투 현상을 관측하고자 하였다. 기체 압력이 벤토나이트의 팽윤압(swelling pressure)의 크기와 유사할 때 기체 유입량이 급격하게 증가하는 기체 돌파(gas breakthrough)가 발생하였고, 밀도가 높은 시료의 기체 돌파 압력(gas breakthrough pressure)이 더 크다는 것을 관측하였다. 또한, 통로로 유입된 기체가 시료 내 별개의 공극에 잔존 기체로 존재할 수 있고 기존 용해된 기체의 확산을 통한 이동과는 달리 소수의 미세 균열에 의한 통로를 통해 기체가 이동한다는 것을 관측하였다. Tanai et al.(1996)은 Fig. 2의 시험 장치를 활용하여 포화 조건에서의 일본산 벤토나이트 Kunigel V1과 프랑스산 Fo-Ca clay 시료를 대상으로 기체 주입 시험을 수행하였다. 기체 주입부 및 유출부에서의 기체 유동 속도와 압력을 측정하였으며, 돌파 압력과 팽윤압의 관계, 기체 투수계수를 분석하였다. 벤토나이트 시료의 팽윤압이 증가할수록 기체 돌파가 발생하기 위해 더 큰 기체 압력이 요구되었고, 두 벤토나이트의 기체 투수계수는 10^-18~10^-21 m² 범위의 값을 보였다. 또한, 첫 번째 기체 돌파 발생 이후 시료를 다시 포화시켰을 때의 기체 돌파 압력이 이전의 값과 비슷하다는 결과를 토대로 기체 주입 중단 시 벤토나이트의 팽윤에 의해 기존 기체 흐름 통로가 폐쇄될 수 있다고 결론지었다.

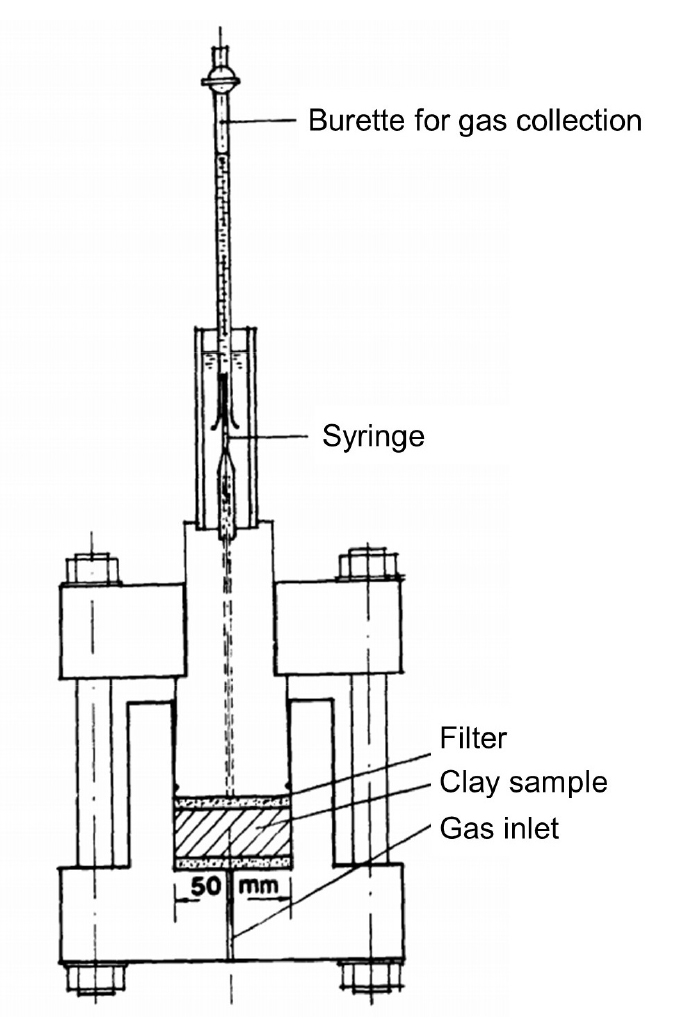
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F1.jpg

Fig. 1

Schematic view of experimental apparatus for gas migration utilizing MX-80 bentonite sample (Pusch and Forsberg, 1983)

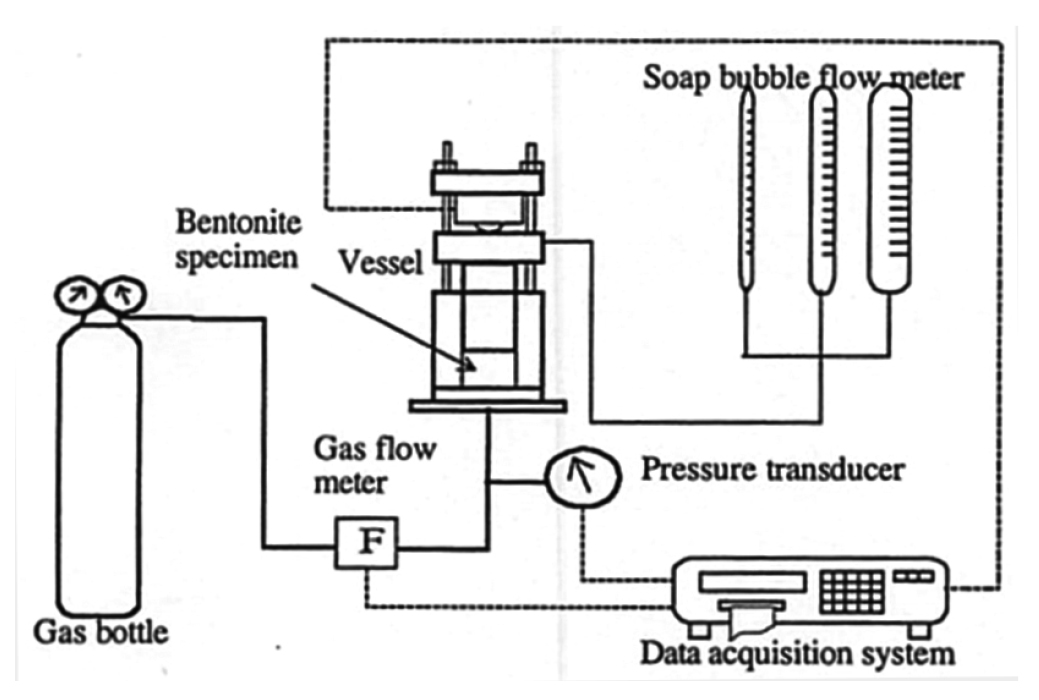
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F2.jpg

Fig. 2

Schematic view of experimental apparatus for gas migration utilizing Kunigel V1 bentonite sample (Tanai et al., 1996)

Volckaert et al.(1995)과 Horseman et al.(1996, 1999)은 각각 Pontida/Boom clay와 MX-80 벤토나이트 시료를 활용하여 기체 주입 실내시험을 수행하였다. 이들의 연구에서는 간헐적인 파열 형태(burst-type)의 거동, 즉 기체 이동 통로의 생성 및 폐쇄에 따른 불연속적인 기체 유출 현상을 관측하였다. 특히, Horseman et al.(1999)은 다수의 개별 기체 이동 통로가 생성되는 현상과 포화된 벤토나이트 시료에서의 기체 유입 압력이 팽윤압과 공극수압(porewater pressure)의 합과 유사하다는 것을 관측하였고, 기체 유입을 위한 임계 압력의 매우 큰 계측 결과를 토대로 포화 상태의 벤토나이트 내 기체 이동 시 공극수의 직접적인 변위는 발생하지 않고 일반적인 2상 유체 유동이 불가능하다고 결론지었다.

Donohew et al.(2000)은 점토 시료 내 기체가 유입된 이후 초기 기체 유입 압력보다 낮은 압력으로 기체 주입이 반복될 때 기체 이동 통로가 다시 개방된다는 것을 관측하였다. Harrington and Horseman(2003)과 Horseman et al.(2004)은 일정 체적 조건의 벤토나이트 시료에 대한 기체 주입 시험에서 위와 동일한 현상을 관측하였으며, 기체의 유입이 중단되는 차단 압력(shut-in pressure)과 자발적인 기체 흐름 통로 폐쇄 현상을 관측하였다. 기체 유입이 중단되면 기체 압력과 기체 유출 속도는 점차 감소하게 되고 기체 이동 통로는 자발적으로 폐쇄되면서 인장 강도(tensile strength)가 다시 생기게 된다. 차단 압력은 기체 유출 속도가 0일 때의 조건에 수렴하는 기체 압력으로 정의되며, 점토 내 기체가 유동할 수 있는 최소한의 압력을 의미한다.

Graham et al.(2002)은 다양한 건조밀도, 함수비, 포화도 조건, 구속 조건에서의 벤토나이트 시료를 활용하여 기체 주입 시험을 수행하였으며, 벤토나이트 시료의 포화도가 낮아지면 기체 돌파 압력이 급격하게 감소한다는 것을 관측하였다. 또한, 기체 주입 압력을 일정하게 유지하였을 때, 낮은 주입 압력에 비해 큰 주입 압력에서의 기체 돌파 발생이 더 빠르고 시료의 건조밀도가 증가할수록 기체 돌파 발생이 늦어진다는 것을 관측하였다. 단기간에 점진적으로 압력을 증가시키는 조건에서의 기체 주입 시험과 비교 시, 장기간 일정한 압력으로 기체를 주입했을 때 더 낮은 압력에서 기체 돌파가 발생하였다.

Harrington(2016)과 Harrington et al.(2017)은 각각 1차원과 3차원 구상류(spherical flow) 기체 주입 실내시험을 수행하였으며, 투수계수가 매우 낮은 점토질 기반암 및 벤토나이트에서의 기체 이류에 의한 이동 현상을 파악하고자 하였다. 두 실험에서는 Fig. 3과 같은 동일한 장치가 사용되었으며, 일정 체적 조건으로 실험이 수행되었다. 실험에는 MX-80 벤토나이트 시료(건조밀도 1.56 kg/m³)가 사용되었고, 기체로는 헬륨(He)을 사용하였다.

Harrington(2016)의 1차원 기체 주입 시험은 벤토나이트 시료를 실험 장비에 삽입한 후 기체를 주입하기 전 공극 필터(pore filter)를 통해 증류수를 공급하여 충분한 팽윤 상태가 되도록 초기 수화 과정을 거쳤다. 이후 기체의 주입 및 압축으로 인해 기체 주입 압력이 점진적으로 증가하여 약 10.5 MPa에 도달했을 때(63.5일 차) 기체 돌파 흐름이 발생하였다(Fig. 4(a)).

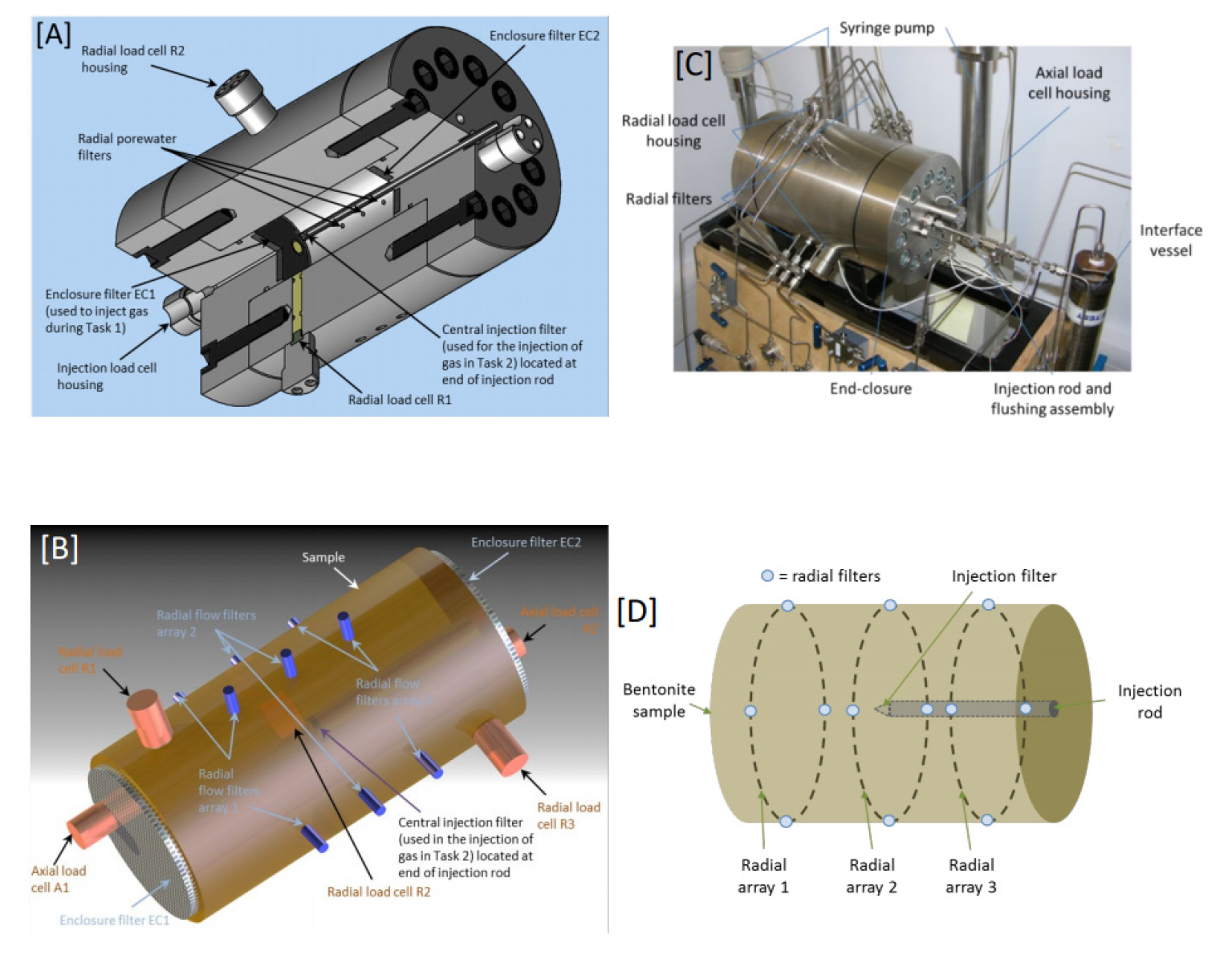
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F3.jpg

Fig. 3

(a-b) Schematic view of gas migration apparatus used for 1- and 3-dimensional tests, (c) photograph of experimental setup, and (d) schematic view of the location of injection and radial filters (Harrington, 2016, Harrington et al., 2017)

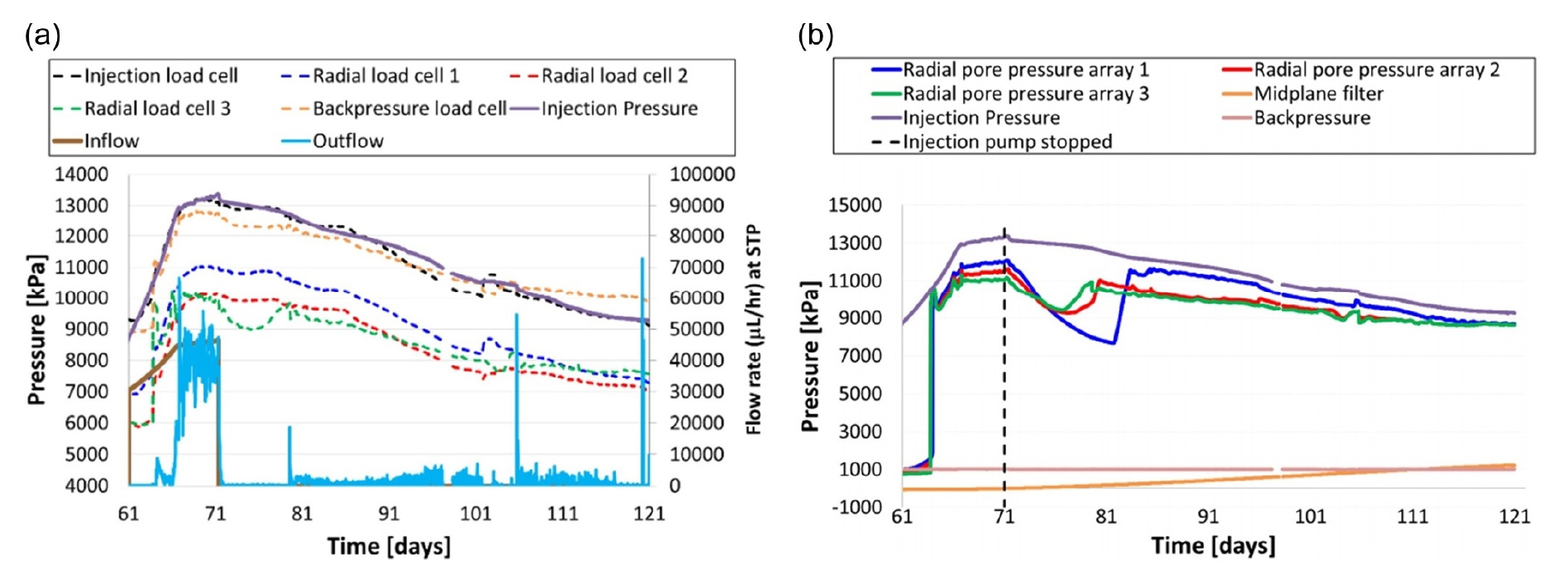
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F4.jpg

Fig. 4

Results monitored during 1-dimensional gas migration test. (a) Total stress and gas flow rate at standard temperature and pressure (273.15 K and 101.325 kPa, respectively) and (b) pore pressure, measured prior to and after gas breakthrough occurrence (Harrington, 2016, Tamayo-Mas and Harrington, 2020)

기체 돌파 발생 직후 주입부(Fig. 3(b)의 EC1)에서 가장 가까운 열(array 1)에서의 공극압보다 가장 먼 열(array 3)에서의 공극압이 먼저 상승하였으며(Fig. 4(b)), 이는 벤토나이트 시료 내 기체 흐름 통로의 생성이 균일하지 않다는 것을 나타낸다. 전응력이 급격하게 증가한 이후, 전응력의 변화는 기체 주입 압력의 시간에 따른 변화와 유사한 경향을 보였다(Fig. 4(a)).

기체 주입 중단(71일 차) 이후 기체 주입부에서의 압력이 감소하기 시작하였으며, 기체의 유출 속도가 급격하게 감소함에 따라 전응력과 공극압이 감소하였다. 그러나, 81일 차 이후 공극압이 반등한 것으로 보아 기체 주입 중단이 공극압의 자발적 변화의 유일한 원인은 아니라고 판단할 수 있다. 기체 주입 중단 이후 기체의 유출이 산발적으로 발생하는 것으로 보아 새로운 기체 흐름 통로가 지속하여 생성 및 폐쇄된다는 것을 파악할 수 있으며, 일부 기체 유출 발생 시 전응력 및 공극압의 변화와 직접적인 관련성을 보였지만, 이외의 기체 유출 발생 건에서는 관련성을 보이지 않은 것으로 보아 기체 이동 통로가 개별적으로 생성될 수 있다는 것을 파악할 수 있다.

1차 기체 돌파 발생 이후 기체 유출량이 감소함에 따라 공극압과 응력 또한 일시적으로 감소하였으며, 이는 기체 이동 통로의 불안정성을 나타낸다. 이후 기체 주입 압력이 더욱 증가하여 약 12 MPa에 도달했을 때(약 65일 차) 기체 유출량이 다시 급격히 증가하기 시작하였고, 기체 주입 압력이 약 13 MPa에 도달했을 때 기체 주입 속도와 유출 속도가 대략적으로 수렴하여 준안정 상태(quasi-steady state)에 도달함에 따라 기체 주입 압력, 전응력, 공극압의 증가 추세가 감소하였다.

1차원 기체 주입 시험에서는 기체 돌파 흐름 발생 이전의 경우, 시료의 역학적 특성에 대한 기체의 수리적 특성의 영향이 미미하였으나, 기체 돌파 흐름 발생 이후 시료의 전응력과 공극압의 변화는 기체 압력과의 밀접한 관계성을 보였고, 기체 주입 중단 이후에도 전응력, 공극압, 기체 압력이 유사한 추세로 감소하면서 계속해서 수리-역학적 관계성을 나타냈다.

Harrington et al.(2017)의 3차원 구상류 기체 주입 시험에서는 시료의 중심부에 위치한 기체 주입을 위한 관(injection rod) 끝의 주입 필터를 통해 기체가 주입되었으며, 기체 주입 전 시료의 팽윤 증진을 위해 물을 주입하여 시료가 포화 상태가 되도록 하였다. 3차원 구상류 기체 주입 시험의 경우, 측면부의 공극 필터로만 기체 유출이 가능하게 하였다.

기체 주입 초기 단계(Stages [1]-[3])에서는 기체 압력 증가에 따라 응력이 최대 8 MPa까지 증가하였으나, 이후 계속된 가압에도 응력의 증감이 거의 없는 안정화 상태가 되었으며, 기체 압력이 최대 응력을 약간 초과(Stage [9])했음에도 안정 상태가 유지되었다(Fig. 5(a)). 기체 충전을 위한 감압 이후 다시 가압하는 단계(Stage [11])에서는, 기체 압력이 시료의 최대 응력(R2)을 초과하는 743.5일 차부터 증가하는 기체 압력에 따라 전체 응력이 증가하는 수리-역학적 복합 거동을 보였다(Fig. 5(b)).

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F5.jpg

Fig. 5

Results monitored during spherical flow gas migration test. (a) Variations in total stress and pore pressure up to day 700 (stages [1]-[10]). Variations in (b) total stress and (c) gas flow rate at standard temperature and pressure (273.15 K and 101.325 kPa, respectively), measured from day 735 to day 835 (Harrington et al., 2017, Tamayo-Mas and Harrington, 2020)

8.05 MPa의 압력에서 첫 번째 기체 유입 발생(747.3일 차) 직후 주입 압력이 약간 감소하였고, 균일하지 않은 기체 흐름 통로 생성으로 인해 array 1에서는 기체 유출 분포가 거의 발생하지 않았으며(Fig. 5(c)), 다양한 크기 및 방향의 통로 생성에 따라 응력이 증가하거나 감소하는 복잡한 거동이 발생하였다(Fig. 5(b)). 이후 점토 물질의 자체적인 통로 밀봉 특성으로 인해 기체 유출이 감소하게 되어 기체 투수계수가 저하되고, 기체 압력이 다시 증가하였다.

756.9일 차에 9.72 MPa의 기체 압력에서 첫 번째 주요 기체 돌파가 발생하였다. 측면부의 첫 번째, 두 번째 열(arrays 1, 2)을 통해 기체가 빠르게 유출됨에 따라 기체 압력이 9.02 MPa로 감소하였으나, 기체 통로의 불안정성 및 폐쇄로 인해 다시 기체 압력이 증가하였다(Fig. 5(c)). 이후 유사한 거동으로 761일, 764일 차에 기체 돌파가 추가 발생하였다. 기체 압력이 다시 증가하는 동안 기체 통로 불안정성으로 인해 응력의 증감 추세가 계속 변동되었고 여러 차례의 불규칙한 기체 유출이 관측되었다.

세 번째 기체 돌파(764일 차) 이후 측면부 array 3으로 기체 유출이 집중되었다(Fig. 5(c)). 통로 전파의 감소로 인해 응력장(stress field)의 교란이 줄어들고, 축 응력 A1을 제외한 나머지 응력들은 비슷한 범위로 수렴하는 경향을 보였다(Fig. 5(b)). 이후 통로 폐쇄에 의한 가압으로 인해 기체 압력이 9.88 MPa까지 상승하였다. 이후 기체 주입 속도와 유출 속도가 대략 수렴하여 안정화됨에 따라 연속되는 기체 주입에도 불구하고 압력이 계속해서 감소하였으며, 응력 또한 이와 유사한 추세로 감소하였다. 805일 차 이후 기체 주입 압력은 최대 응력(축 응력, A2)과 거의 유사한 값을 가지며, 기체 유출이 특정 열(array 3)에 집중(국부적 기체 흐름)되는 반면에 기체 흐름은 상대적으로 안정적으로 유지되어 이전보다 적은 변동성을 나타냈다.

3차원 기체 주입 시험에서는 1차원 기체 주입 시험과는 달리 기체 주입 초기 단계에서 기체 주입 압력 증가에 따라 응력이 증가하였으나, 일정 압력에 도달한 이후에는 1차원 주입 시험과 유사하게 기체 가압 시에도 응력의 변화가 적었으며, 기체 압력이 시료의 최대 응력을 초과하는 시점부터 가압에 따라 응력이 증가하는 수리-역학적 복합 거동을 나타냈다. 1차원 기체 주입 시험과 비교 시 기체 돌파 흐름 발생 전후 시료의 역학적 거동이 더 복잡하다는 차이를 보였으나, 기체 돌파 발생 이후 기체 주입 속도와 유출 속도가 수렴할 경우 수리-역학적 거동이 안정화된다는 공통점을 나타냈다.

Gallé(1998, 2000), Gallé and Tanai(1998), Harrington and Horseman(1999), Hoch et al.(2004), Cuss et al.(2012), Harrington et al.(2012), Graham and Harrington(2014) 등은 앞서 기술한 벤토나이트 시료를 활용한 기체 주입 시험과 유사한 실내시험을 수행하였으며, 이들 실험으로부터 관측된 점토 물질 내 기체 이동 현상은 기존 실험의 결과와 크게 다르지 않았다. 벤토나이트 내 기체 주입 실내시험으로부터 확인된 기체 이동 특성은 다음과 같이 정리할 수 있다(Bond et al., 2018).

- 기체 이동 통로의 생성 및 폐쇄에 따른 불연속적인 기체 유출(burst-type)

- 다수의 개별 기체 이동 통로 생성

- 기체 주입 시 무시할 정도로 작은 액체의 변위: 시료 포화 상태 유지, 즉 국부적으로 생성된 통로(균열)를 통해 기체 이동

- 기체 유입 압력은 팽윤압과 공극수압의 합, 즉 전응력(total stress)과 유사하거나 관계성이 있음

- 기체의 돌파 흐름 발생 이후 더 낮은 기체 압력에서도 기체 흐름 지속

- 기체 흐름을 중단시키는 차단 압력은 전응력과 유사, 기체 주입 중단 시 기체 압력이 차단 압력으로 점근적으로 감소

- 기체 흐름 통로의 자발적인 폐쇄 또는 전환(통로의 불안전성)

- 포화도 감소 시 기체 돌파 압력이 감소하며, 포화도 0.93 이하에서는 돌파 압력이 작은 상수에 수렴

- 유입된 기체는 폐쇄된 통로 내 공극/균열에 잔류할 수 있고, 기존 돌파 압력보다 낮은 압력에 의해 통로 다시 개방 가능

2.2 현장시험

벤토나이트 완충재로의 기체 유출은 공극수로의 핵종 이동을 유발할 가능성이 있기 때문에 공학적방벽의 성능 평가 시 벤토나이트 완충재에서의 기체 이동과 핵종 이동 간 상호작용 가능성은 고려해야 할 중요한 사안 중 하나이다. 앞서 언급하였듯이, 여러 실내시험을 통해 완충재 내 기체 이동 특성의 이해를 증진시켰지만, 실험적 경계 조건에 대한 민감성, 실험 계측 자료의 실험 규모에 따른 의존성 등 여러 불확실성이 존재한다(Horseman et al., 2004). 이러한 문제의 대안으로 지하처분연구시설의 시추공에서 현장시험이 수행되었으며, Vomvoris et al.(2003)과 Sellin and Harrington(2006)은 각각 Gas Migration Test(GMT), Large scale gas injection test(Lasgit)를 통해 현장에서의 기체 이동 거동 특징을 파악하고자 하였다.

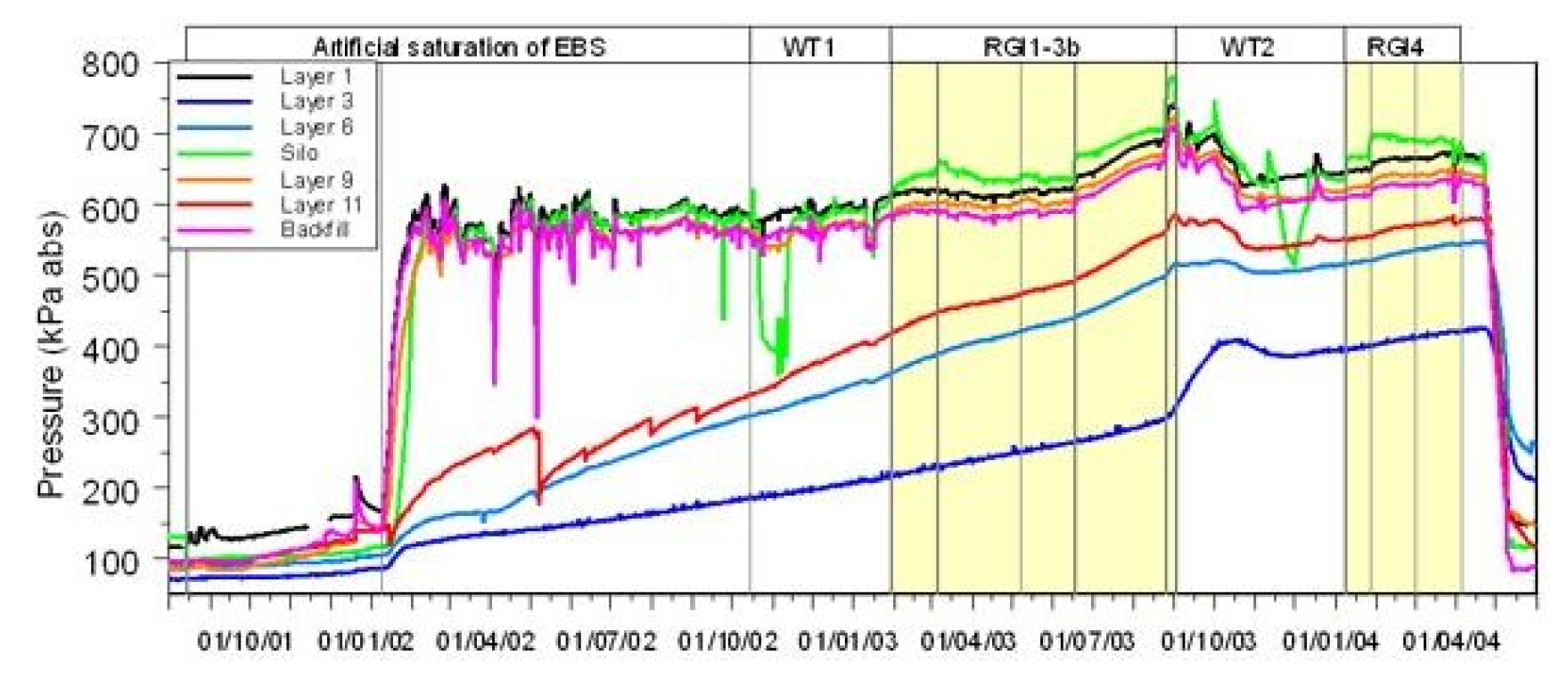
GMT는 스위스의 Grimsel underground laboratory에서 수행되었으며, 화강암을 수직 방향으로 굴착한 시추공에 설치된 콘크리트 사일로로부터 모래 –벤토나이트 혼합물 완충재와 암반으로 방출되는 기체의 거동 특성을 파악하고자 하였다(Fig. 6). GMT에서는 1:10 축소 규모로 콘크리트 사일로를 설치하였으며, 사일로와 완충재 위에 위치한 터널은 모래와 자갈 혼합물 뒷채움재로 채워졌다. 실험에서는 공극압, 응력, 온도, 체적함수비의 시간에 따른 변화가 관측되었다. 기체를 주입하기 전 공학적방벽과 GMT 동굴 주위를 포화시키기 위해 2001년 8월부터 공학적방벽의 가장 하부의 모래층과 뒷채움재로 물을 주입하였고(Ando et al., 2002), 2003년 1월부터 질소 가스를 이용한 기체 주입 시험을 수행하였으며, 2004년 4월에 실험이 종료되었다(Olivella and Alonso, 2008).

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F6.jpg

Fig. 6

Concept of the GMT experiment at the Grimsel underground laboratory (Olivella and Alonso, 2008)

GMT에서는 두 단계(RGI1-RGI3b, RGI4a-c)로 나누어 기체 주입 시험이 진행되었다. 첫 번째 단계에서는 2003년 1월 29일 0.025 mg/s의 속도로 기체 주입을 시작하여(RGI1), 3월 5일 0.05 mg/s(RGI2a), 5월 7일 0.1 mg/s(RGI2b), 6월 17일 1 mg/s (RGI3a), 8월 25일 5 mg/s(RGI3b)까지 단계적으로 주입 속도를 증가시켰으며, 약 8.5 m³의 질소 가스를 주입한 후 9월 2일에 기체 주입을 중단하였다. 두 번째 단계에서는 2004년 1월 8일 0.05 mg/s의 속도로 기체 주입을 시작하여(RGI4a), 1월 27일 1 mg/s(RGI4b)까지 단계적으로 주입 속도를 변화시켰으며, 3월 4일에 기체 주입 배관을 두 개로 분리(RGI4c)하였다.

Fig. 7은 기체 주입 전 공학적방벽 포화 단계부터 기체 주입 시험까지 GMT 현장시험의 전 과정 동안 계측된 공극압을 나타낸다. 포화 단계 이후 기체가 주입됨에 따라 전반적으로 기체 압력이 상승하는 경향을 보였으나, 일부 센서에서는 기체 주입 속도가 0.1 mg/s 이하인 RGI2b 단계까지 기체 압력의 변화가 미미하였다. 최대 기체 압력은 0.8 MPa 이하로 매우 작았으며, 기존 실내시험과는 달리 기체 돌파 현상이 관측되지 않았고, 기체 주입 과정에서 체적 함수비의 변화가 거의 없다는 것을 관측하였다.

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F7.jpg

Fig. 7

Variations in liquid and gas pressure measured during the GMT experiment (from grimsel.com)

Lasgit은 스웨덴 KBS-3 처분시스템 개념의 처분공 실규모를 반영하여 스웨덴의 Äspö Hard Rock Laboratory의 지하 420 m의 처분공(깊이 8.5 m, 직경 1.75 m)에서 수행되었으며, 처분공에 실험 장치를 설치한 후 콘크리트 플러그 및 주철 덮개(steel lid)로 처분공을 폐쇄하였다(Fig. 8). 처분용기 표면, 벤토나이트 블록 내부, 처분공 벽면에서 실험 과정 동안의 전응력(32 곳), 공극압(26 곳), 상대 습도(7 곳)의 변화량이 실시간으로 계측되었고, 기체 이동 과정에 대한 이해 증진을 통해 수치모델링 기법을 개선 및 검증하기 위한 정량적인 정보와 양질의 실험 자료를 제공하고자 하였다. 실험 규모 확대에 따른 문제와 기체 이동 및 완충재 거동에 미치는 영향을 분석하는 것을 목표로 기체 주입 시험이 수행되었다(Cuss et al., 2014b). Lasgit은 2005년 2월부터 2012년 7월까지 2726일 (약 7.5 년) 동안 수행되었으며, 기체를 주입하기 전 처분공 내 벤토나이트를 포화 및 안정화시키기 위해 수화 단계를 거친 후 기체 주입 시험을 수행하였다. 총 세 차례의 기체 주입 시험이 수행되었으며, 실험의 전체 일정은 Table 1과 같다. 두 번의 실험에서는 처분용기 하부의 주입 필터(Section 5의 FL903; Fig. 8 참조)를 통해 기체를 주입하였고, 세 번째 실험은 상부의 주입 필터(Section 9의 FU910)를 통해 기체를 주입하였다.

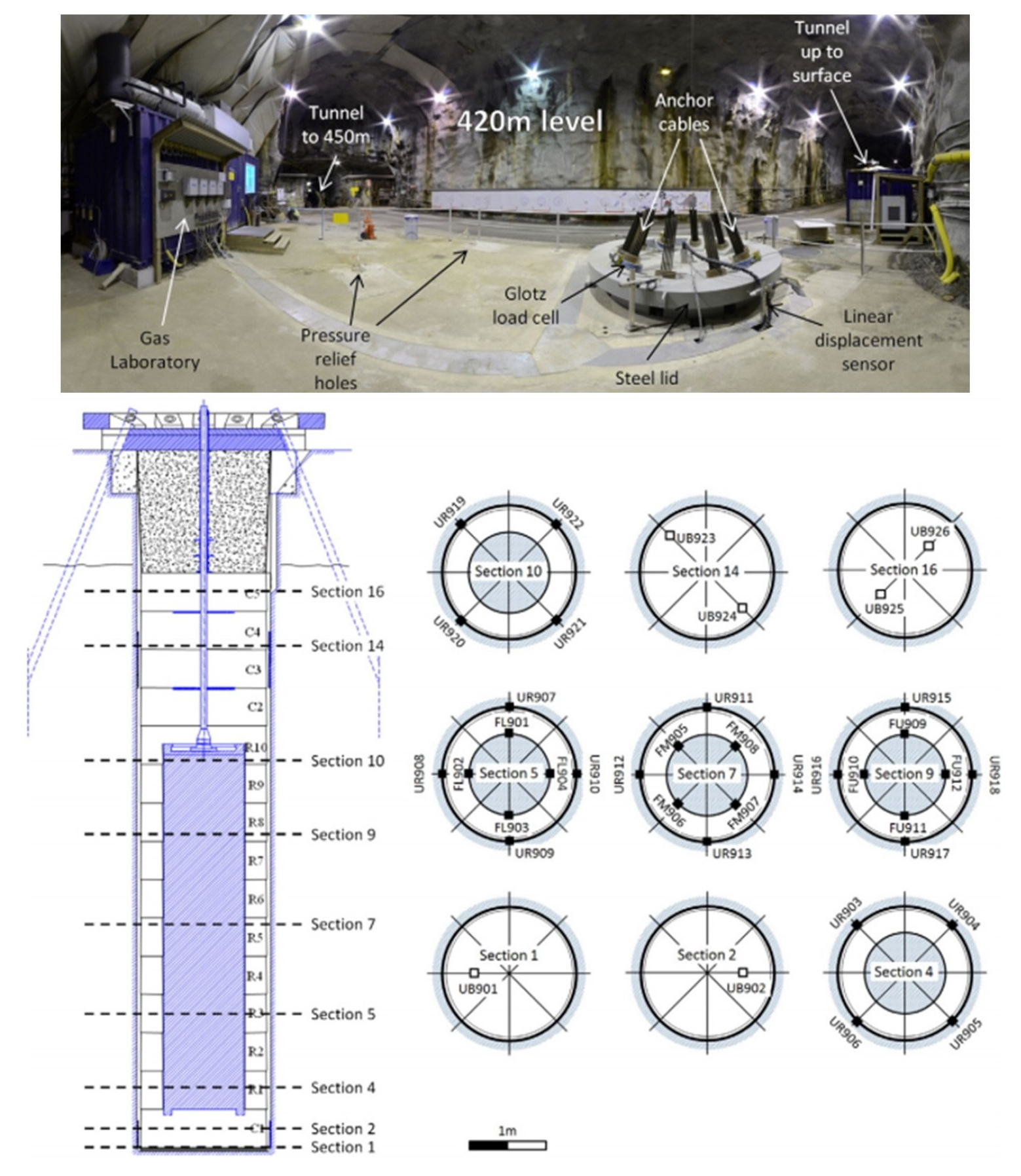
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F8.jpg

Fig. 8

Schematic view of the test site and test devices of Lasgit experiment (Sellin and Harrington, 2006, Cuss et al., 2011)

Table 1.

Schedule of Lasgit experiment including three preliminary gas injection tests (Cuss et al., 2014b)

Phase of test	Duration
• Artificial hydration phase 1	• From Day 0 to 843
• 1st Gas test ○ Hydraulic test ○ Gas injection test ○ Hydraulic test	• From Day 843 to 1110 ○ From Day 843 to 917 ○ From Day 917 to 1010 ○ From Day 1010 to 1110
• Artificial hydration phase 2	• From Day 1110 to 1430
• 2nd Gas test ○ Hydraulic test ○ Gas injection test ○ Hydraulic test	• From Day 1430 to 2019 ○ From Day 1473 to 1577 ○ From Day 1606 to 1964 ○ From Day 1964 to 2019
• 3rd Gas test ○ Hydraulic test ○ Leak off test ○ Gas injection test ○ Hydraulic test	• From Day 2072 to 2726 ○ From Day 2085 to 2141 ○ From Day 2141 to 2257 ○ From Day 2257 to 2673 ○ From Day 2673 to 2726

첫 번째 기체 주입 시험은 실험 917일 차부터 시작되었으며, 1.26×10^-3 m³의 헬륨 가스가 주입되었다. 924일 차부터 완충재로 기체가 유입되었으며(Fig. 9(a)), 기체 유입 압력은 0.65 MPa로 실내시험에서 계측된 값에 비해 작았는데 이는 완충재의 불완전한 수화, 점토 내 응력장의 이질적 특성에 기인한 것으로 판단된다. 기체 가압 중단 후 일정 압력을 유지했을 때(930일 차), 벤토나이트로의 기체 주입량이 급감하였으며(Fig. 9(a)), 이는 일정 기체 압력 조건에서는 주요 기체 통로의 전파가 중단되고 기체 투수계수가 감소된다는 것을 나타낸다. 이후 소량의 기체가 지속적으로 유입되는데, 기체가 작은 균열을 통해 이동하였다고 판단된다. 952일 차부터 기체가 다시 가압되었고, 972일 차에 5.66 MPa의 최대 기체 압력에 도달한 후 벤토나이트로의 기체 유입량 급증으로 인해 기체 압력이 감소하였으며, 기체 유입 속도의 감소와 증가가 반복되는 동적 거동을 보였다(Fig. 9(b)). 이는 기체 통로의 불안정성을 나타내며, Horseman et al.(1999)와 Harrington and Horseman(2003)의 실내시험 결과와 유사한 거동을 나타낸다. 이후 기체 주입 압력은 감소하여 5.5 MPa의 준정상 상태에 도달하였다.

두 번째 기체 주입 시험은 1606일 차부터 수행되었으며, 1.3 MPa의 초기 압력으로 기체를 주입하였다(Fig. 9(c)). 기체 주입 압력을 증가시킨 이후 일정 기간 동안 압력을 유지시키는 것을 세 차례 수행하였으며, 첫 번째 기체 주입에서 관측된 거동(Fig. 9(a))과 유사하게 일정 압력 유지 시 기체 주입량이 급격히 감소하였다. 기체 유입 압력은 첫 번째 시험에 비해 상당히 큰 1.3 MPa로 관측되었다. 1742일 차부터 기체가 다시 가압되었고, 1767일 차에 5.87 MPa의 최대 기체 주입 압력에 도달하였으며(Fig. 9(d)), 최대 압력 도달 직후 압력 감소 과정에서 기체 유입 속도의 동적 거동이 관측되었다. 이는 첫 번째 기체 주입 시험에서 관측된 거동(Fig. 9(b))과 유사하였다.

세 번째 기체 주입 시험은 2257일 차부터 수행되었고, 1 MPa의 초기 압력으로 기체를 주입하기 시작한 후 두 번째 기체 주입 시험의 순차적 압력 증가 및 유지 단계(Fig. 9(c)), 최대 기체 주입 압력 발생 단계(Fig. 9(d))와 유사하게 실험을 수행하였으며, 두 번째 기체 주입 시험과 유사한 거동이 관측되었다. 기체 유입 압력은 초기 기체 주입 압력(1 MPa)과 동일하였고, 5.4 MPa의 최대 기체 주입 압력이 관측되었다.

Lasgit에서는 처분시스템의 실제 규모를 반영한 현장 기체 주입 시험을 통해 현장에서의 기체 이동의 거동을 파악하고 기체 이동이 완충재의 역학적 거동에 미치는 영향을 분석하고자 하였다. 최대 기체 주입 압력 도달 직후 벤토나이트 내로 기체의 급격한 유입으로 인한 압력 감소 과정에서 기체 이동 통로의 생성 및 패쇄가 불규칙하게 발생되는 현상, 즉 통로의 불안정성이 관측되었고, 이는 Horseman et al.(1999)와 Harrington and Horseman(2003)의 실내시험 결과와 유사한 거동을 나타낸다. 그러나, 실내시험 결과와 대비하여 상당히 낮은 기체 유입 압력이 관측되었는데, 이는 완충재의 불완전한 포화 상태에 의한 완충재의 낮은 응력을 원인으로 볼 수 있다. 처분시스템 실규모 기체 주입 시험을 통해 기체와 매질의 수리-역학적 복합 거동 특성이 어느 정도 입증되었으나, 수리적 특성과 역학적 특성 사이의 상호 의존성과 복합 거동의 정확한 특성을 파악하기 위한 연구가 추가적으로 필요할 것으로 판단된다.

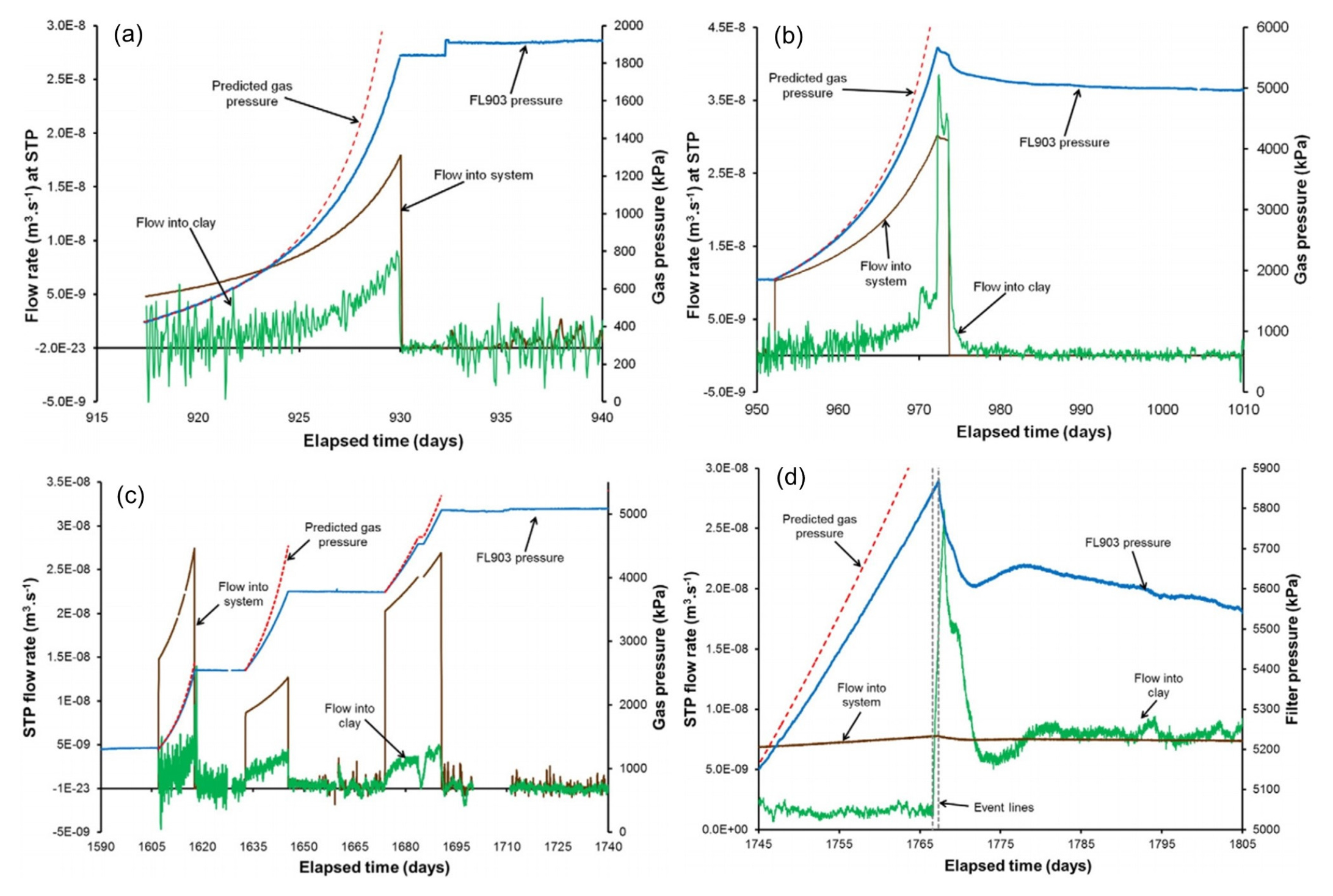
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F9.jpg

Fig. 9

Variation in STP flow rate and gas pressure measured at FL903 during Lasgit test. First gas injection: (a) the first and (b) the second stage of gas injection. Second gas injection: (c) the first and (d) the second stage of gas injection (Cuss et al., 2011)

3. 전산 모사 해석 연구 동향

이 장에서는 포화된 벤토나이트 내 기체 이동 메커니즘 규명을 위해 수행된 전산 모사 해석 동향을 문헌 조사를 통해 정리하고 이를 통해 점토 물질 내 기체 이동 현상 규명을 위한 전산 모사 연구의 방향성을 제시하였다.

3.1 기체 이동 전산 모사 개요

앞서 언급한 바와 같이 포화된 벤토나이트 내 기체 이동 메커니즘 규명을 위한 전산 수치 해석 연구는 심층처분시스템을 활용한 사용후핵연료의 효율적이고 안정적인 관리를 위해 필수적이기 때문에, 기체 이동 현상 모사를 위한 다양한 전산 수치 모델 개발 연구가 수행되었다. Guo and Fall(2021)은 현재까지 개발된 전산 수치 모델에 대해 정리하여 소개한 바 있으며, 이를 참조하여 현재까지 제안된 기체 이동 전산 모델의 특징에 대해 정리하고, 기존 연구의 한계점을 분석하여 향후 전산 모사 연구 방향에 대해 정리하였다. 앞서 2장에서 서술한 바와 같이 포화 벤토나이트 내 기체의 생성 및 이동 현상은 기존 사질토 또는 암반에서의 일반적인 이상 유동 흐름과 다른 특징을 가진다. 특히, 상대적으로 낮은 투수계수와 높은 모관 흡수력으로 인해 공극 내 기체가 응축되어 기체 압력이 증가하는 현상과 공극 내 기체 압력이 공극수압과 팽윤압의 합과 같아지는 순간 균열이 발생하여 이를 통해 기체가 순간적으로 이동하는 기체 돌파 현상이 가장 특징적인 거동이다(Olivella and Alonso, 2008). 앞선 내용들을 정리해 보면 벤토나이트와 같이 낮은 투수계수를 갖는 점토 물질 내 기체 이동 메커니즘 규명을 위한 전산 수치 모델 개발을 위해서는 기체 발생 또는 유입에 의한 공극 내 기체 압력 증가와 포화 단계에서 점토의 팽윤 특성을 고려하여 이에 따른 균열의 발생 및 전파 현상을 모사할 수 있도록 수리-역학적 복합 거동을 필수적으로 고려해야 함을 알 수 있다(Guo and Fall, 2021).

3.2 전산 수치 해석 적용 모델

벤토나이트와 같은 점토 물질 내 기체 이동 예측 모델은 선행 연구자들로부터 다양하게 개발되었지만, 여전히 기체 이동을 모사하기에는 제한적이며 기체 이동에 대한 기본 메커니즘 또한 완벽하게 정립되지 않아 대다수의 연구자들이 공감할 수 있는 기체 이동 예측 모델은 정립되지 않은 상황이다(Harrington et al., 2017, Horseman et al., 1999, 2003, Graham et al., 2012, Kim et al., 2021, Tamayo-Mas et al., 2021). 이 절에서는 점토 물질 내 기체의 이동 거동 모사를 위해 기존 문헌들에서 적용한 역학적, 수리학적 구성 모델들을 소개하고 각각의 모델들의 장단점을 정리하여 해석 조건에 따른 적용 가능 모델을 제안하였다.

3.2.1 역학 모델(mechanical model)

점토 물질 내 기체의 이동 메커니즘 규명을 위한 전산 모사 시 역학적 거동은 매질 전체의 응력-변형률 거동을 표현하는 역학 모델과 매질 내 국부적인 거동 모사를 위한 역학 모델로 구분할 수 있다. 매질 전체의 역학적 거동 모사를 위해 주로 사용되는 역학 모델로는 탄성(elasticity), 탄소성(elasto-plastic), 열탄소성(thermo-elasto-plastic) 모델 등이 있다. 가장 단순한 형태의 탄성 모델에서 상대적으로 복잡한 형태의 열탄소성 모델로 갈수록 더 실제와 가까운 거동을 모사할 수 있다는 장점이 있지만, 반대로 입력 인자의 수와 해석 수행 시간이 길어진다는 단점을 가지고 있다. 따라서, 전산 모사 해석 연구에서는 해석 조건과 목적에 맞게 역학 모델을 선택해야 한다. 탄성모델은 Hooke 법칙을 기반으로 하여 매질의 응력-변형률 관계를 나타내는 모델로써, 비교적 단순한 형태이지만 포화된 벤토나이트 내 기체 주입 실험 모사를 위한 전산 모델 개발 및 검증 국제 공동 연구인 DECOVALEX 2019 Task A에서 Table 2와 같이 실험 시 관측된 현상들을 비교적 잘 모사한 사례가 보고된 바 있다(Tamayo-Mas and Harrington, 2020).

DECOVALEX 2019 Task A에서 탄성 모델을 통해서도 높은 예측 신뢰도를 보인 이유는 해석 조건인 포화된 벤토나이트의 경우 이미 팽윤 거동이 진행된 이후의 상태로 추가적인 팽윤 거동이 상대적으로 적어 기체 주입에 따른 매질의 응력-변형률 거동이 선형에 가깝게 거동하기 때문이라고 판단된다. 하지만, 탄성 모델은 불포화 조건에서의 점토의 포화도 혹은 흡입력(suction pressure)의 변화에 따른 체적변형계수(bulk modulus)의 변화를 고려할 수 없다는 단점이 있다(Lee et al., 2020a). 이러한 단점을 극복할 수 있는 모델로 포화도에 따른 흡입력 변화와 이를 반영한 체적변형계수를 고려할 수 있는 탄소성 역학 모델인 초기 barcelona basic model (BBM)이 modified cam clay model (MCCM)을 기반으로 하여 제안되었으며(Alonso et al., 1990), Gens(1995)에 의해 온도 변화에 따른 점토 물질의 팽윤 특성 변화를 추가로 고려할 수 있는 열탄소성 모델로 수정 보완되었다. 이러한 특징으로 인해 BBM은 열-수리-역학 거동이 복합적으로 작용하는 사용후핵연료의 심층처분시스템 내 완충재의 장기 성능 평가를 위한 전산 해석 분야에 적합하다고 알려져 있으며(Lee et al., 2019), 다양한 예제 및 실내외 실험 모사를 통해 모델 적용성과 예측 신뢰도에 대한 검증이 수행된 바 있다(Rutqvist et al., 2011, Lee et al., 2020b, 2020c).

Table 2.

Comparison of pore pressure distribution prediction of numerical models suggested in DECOVALEX-2019

	BGR/ UFZ-E	CNSC-PD	KAERI-D	NCU/ TPC-V	UPC/ Andra-ED	LBNL-D	Quintessa /RWM -ECap
Constitutive model	Elasticity	Elasto-plastic damage	Elastic damage	Visco-elastic	Elastic with dilatancy	Elastic-brittle damage and fracture	Elasticity
1D test (Stage 1)
Quiescence	✕	○	○	○	○	○	△
Gas breakthrough	△	✕	△	✕	△	✕	△
Peak value	△	△	○	○	○	○	○
Negative decay	○	○	○	○	○	○	○
3D test (Stage 2)
Quiescence	✕	△	○	○	△	△	○
Gas breakthrough	○	✕	○	○	△	○	○
Peak value	✕	✕	○	○	✕	✕	○
Negative decay	○	✕	✕	△	○	✕	✕
Other indicators
Heterogeneity	✕	○	✕	✕	○	✕	✕
Number of Calibration parameters	-	18	5	7	12	2	12
Gas flux	✕	✕	○	✕	○	○	○

* ○: Well matched (or considered) △: Approximate matched ✕: Poorly matched (or Not considered)

팽윤 모델(swelling model)

앞서 언급한 것처럼, 점토 물질 내 기체 이동 모사를 위해서는 포화도 변화에 따른 점토의 팽윤 특성을 고려한 해석이 필요하다. 점토 매질의 포화 과정에서의 점토의 팽윤 특성에 의해 균열의 생산 또는 생성된 균열의 자가 치유(self-sealing behavior) 및 폐쇄(closure) 현상이 발생하게 되고 이는 매질 내 수리 역학적 특성을 변화시키기 때문이다. BBM과 같이 역학 모델 자체적으로 포화도 및 온도 변화에 따른 점토 물질의 팽윤 거동을 고려할 수 있는 모델도 있지만, 탄성 모델과 같이 모델 내에서 자체적으로 팽윤 특성을 반영하기 어려운 경우에는 추가적으로 팽윤 특성을 고려해야 한다. 이러한 탄성 모델을 활용한 해석 시 팽윤으로 인한 체적 변형은 식 (1)과 같이 탄성 체적변형률에 더하는 형식 또는 팽윤 압력을 추가적인 압력항으로 고려하는 방식으로 전산 모델에 팽윤 특성을 반영하고 있다.

(1)

ε_{t} = ε_{e} + ε_{s w}

여기서, ε_t는 총 체적변형률[-], ε_c와 ε_sw는 각각 탄성 및 팽윤 체적변형률[-]이다. 문헌 연구를 통해 탄성 역학 모델과 함께 주로 많이 활용되는 팽윤 모델을 Table 3과 같이 정리하였다.

또한, 실제 점토 물질의 응력-변형률 관계는 선행 압밀 압력에 따라 탄성 거동 혹은 소성 거동하는 특징을 가지고 있다. 위 Table 3에서 언급한 변형률 의존의 팽윤 모델 (식 (2)-(4))을 활용하여 포화도 변화에 따른 체적 변화를 고려할 수 있지만 이를 단순히 탄성 역학 구성 방정식에 적용하였을 때 점토의 비선형성 거동을 충분히 반영하지 못하는 한계가 발생한다. 이러한 부분을 보완하기 위한 방법으로 Lee et al.(2020a)은 비선형성을 고려한 경험식(식 (5))을 제안하였는데 이 또한 포화도 변화에 따른 점토의 팽윤 특성을 완벽하게 모사할 수 없다는 단점이 존재한다. 따라서, 점토 매질의 탄소성 거동과 팽윤 특성을 고려할 수 있는 MCCM 또는 BBM을 활용한 해석이 좀 더 실제와 유사한 거동을 예측할 수 있을 것이라고 판단된다.

Table 3.

Models for swelling in barrier material

Categories	Models for swelling behavior	Eq.	Reference
Nonlinear elastic	$d ε_{s w} = - κ_{s} \frac{d S_{l}}{S_{l} + p_{a t m}}$	(2)	Olivella and Alonso, 2008
Linear elastic	$d ε_{s w} = - K_{s c} d S_{l}$	(3)	Tamayo-Mas et al., 2018
Saturation related	$d ε_{s w} = - β_{s w} d S_{l}$	(4)	Rutqvist et al., 2018
Empirical nonlinear	$P_{s w} = P_{s w, \max} - \frac{C_{1}}{(1 + \exp (\frac{S_{l} - C_{2}}{C_{3}}))} - C_{4}$	(5)	Lee et al., 2020a

Note: ε_sw is the volumetric strain due to swelling, χ_s is the elastic stiffness parameter corresponding to suction, S_l is the saturation, p_atm is the atmospheric pressure, K_sv is the swelling coefficient, β_sw is a moisture swelling coefficient determined with respect to the saturation, P_sw is the swelling pressure, P_{sw, max} is the maximum swelling pressure, and C_i is the fitting parameters for calibration.

손상 모델(damage model)

점토 물질 내 기체의 유출입 또는 지하수 유입으로 인한 포화도 변화는 매질 내 미세 균열을 발생시키고 이러한 미세 균열이 상대적으로 큰 균열과 합쳐져 전체적인 매질의 강도가 저하하게 된다(Fall et al., 2014). 이러한 강도 저하 정도를 설명하기 위해 Kachanov(1958)은 파괴 변수(damage variable, 0 ≤ D ≤ 1) 개념을 도입하여 매질 손상에 따른 탄성계수 감소 개념을 제안하였다. Kachanov는 균열의 발생 및 전파 시의 손상 정도에 따른 매질의 강도 감소를 손상 전/후의 면적 감소비를 대표체적요소(representative volume element, RVE) 개념을 활용하여 손상 전/후의 공극비 변화를 통해 간접적으로 도출하고 이를 Bishop의 유효 응력에 적용하여 매질의 손상 정도를 아래 식 (6)과 같이 제안하였다.

(6)

\tilde{σ} = σ \frac{A}{\tilde{A}} = \frac{σ}{1 - D}

여기서, $\tilde{σ}$ 는 수정된 Bishop의 유효 응력, σ는 Bishop의 유효 응력, A와 $\tilde{A}$ 는 각각 손상 전/후의 면적 그리고 D는 파괴 변수이다. 이후 많은 연구자들로부터 손상 정도에 따른 파괴 변수 산정법에 대한 연구가 수행되었으며 Mazars는 매질의 손상은 압축으로 인한 손상과 인장으로 인한 손상이 각기 다르게 평가된다고 가정하고 매질 전체의 파괴 변수를 아래와 같은 식 (7)과 같이 제안하였다(Mazars, 1984, 1986, Mazars and Pijaudier-Cabot, 1989).

(7)

D = α_{t} D_{t} + α_{c} D_{c}

여기서, D_t와 D_c는 각각 인장 및 압축력에 대한 파괴 변수이고, α_t와 α_c는 각각 인장 및 압축 가중치 계수이다. 또한, Tang et al.(2002)는 파괴 변수를 응력-변형률 관점에서 아래 식 (8), (9)와 같이 인장 또는 압축 응력에 의한 손상 변수 산정식을 제안하였고, Fall et al.(2014)은 이를 암반 매질 내 기체 주입에 따른 균열 발생 예측 모델에 적용하여 그 적용성을 검증하였다.

(8)

D_{t} = \{\begin{matrix} 0 ε_{t 0} \leq ε \\ 1 - \frac{f_{t r}}{E_{0} ε} ε_{t u} \leq ε \leq ε_{t 0} \\ 1 ε \leq ε_{t u} \end{matrix} (인장 영역)

(9)

D_{c} = \{\begin{cases} 0 ε_{c 0} \leq ε \\ 1 - \frac{f_{c r}}{E_{0} ε} ε \leq ε_{c 0} \end{cases} (압 축 영역)

여기서, f_tr과 f_cr는 각각 잔류 인장 및 압축 강도, ε는 단축 인장 변형률, ε_t0(=f_t/E₀)와 ε_c0는 각각 인장 강도(f_t) 및 압축 강도(f_c)에서의 인장 변형률 그리고 ε_tu는 인장파괴 이후의 인장 변형률이다. 위와 같이 파괴 변수 개념을 적용한 모델의 경우 상대적으로 간단하게 균열의 발생 유/무를 고려할 수 있다는 장점이 있지만, 해석 시 요소(element)를 등방성의 탄성체로 가정하기 때문에 파괴 변수를 스칼라 값으로 적용한다. 이로 인해, 균열의 방향성, 틈의 크기, 간격 등의 세부적인 요소들을 반영하기 어렵다는 단점을 가지고 있다(Guo and Fall, 2021).

균열 모델(fracture model)

앞서 기술한 손상 모델은 요소를 등방성의 탄성체로 가정하여 파괴 변수를 스칼라 값으로 고려하였다. 이는 균열의 발생과 전달과정에서 균열의 방향성을 모사하기 어렵다는 단점이 존재하게 된다. 이러한 단점을 보완하고 우선 경로 형성을 모사하기 위해서는 균열 발달 모델에 대한 고려가 필수적이다. 기존 연구에서 적용된 균열 모델은 크게 (i) linear elastic fracture model(LEFM), 그리고 (ii) cohesive zone model(CZM) 등이 있다. 탄성 변형 에너지(elastic strain energy)를 주로 고려한 LEFM의 경우 균열 끝단에 면적이 거의 0으로 수렴하는 현상으로 인해 끝단에서의 응력이 무한대로 상승하는 응력 특이성(stress singularity) 현상이 발생하게 된다. 이는 유한한 인장 강도를 가지며 파괴 시 소성 거동을 보이는 포화 벤토나이트의 균열 모사에는 적합하지 않다(Nash et al., 1998, Swift et al., 2001, Hallett and Newson, 2005). 이와는 달리 균열의 끝단에서의 균열 영향 구간을 두 개의 접착면으로 가정하고 균열 에너지가 두 접착면 사이의 점착력 이상이 될 때 균열이 발생하는 traction separate law(TSL)를 기반으로 하는 CZM 모델은 응력 특이성 현상이 발생하지 않고 비선형의 소성 변형을 고려할 수 있기 때문에 암반의 균열 또는 흙의 건조 균열 모사를 위한 모델로 가장 보편적으로 사용되고 있다. 다만, 점토 매질의 균열 특성 모사를 위한 TSL 입력 인자인 인장 강도와 균열 에너지(fraction energy)에 대한 실험 연구가 부족하여 신뢰도 높은 균열 모사를 위해 점토 매질을 활용하여 TSL 입력 인자 도출을 위한 추가적인 실험적 연구가 수행되어야 한다(Guo and Fall, 2021).

앞서 언급한 연속체 기반의 균열 모델 이외에 Kim et al.(2021)은 불연속체 기반의 rigid-body-spring network (RBSN) 모델을 활용한 점토 매질 내 기체의 이동 모사 해석 접근법을 제안한 바 있다. RBSN 모델은 탄성체를 불연속적으로 나타내어 개별적인 균열과 균열 조직망을 표현할 수 있다는 것이 특징이다(Kawai, 1978). 특히, Fig. 10과 같이 요소망을 Delaunay 삼각분할과 Voronoi 분할 기법을 통해 생성하고 생성된 Voroni 셀 사이 경계면을 통해 발생된 균열의 전파 방향과 균열의 틈 크기 변화를 고려할 수 있기 때문에 점토 매질 내 기체의 주입 실험에서 관측된 균열의 발생에 따른 기체의 팽창 흐름 현상을 모사하기에 적합하다고 판단된다. 일례로 Fig. 11은 점토 매질 내 기체 이동 모사 시 연속체 기반 손상 모델만을 고려한 경우와 RBSN 모델을 적용하여 균열 전파를 모사한 결과의 차이를 보여주는 사례이다. 연속체 기반의 손상 모델을 적용한 경우는 균열 발생에 따른 투수계수 변화 반영 시 주로 등방성(isotropic)의 투수계수를 가정하기 때문에 균열의 전파 방향을 명확하게 모사하기에 어려움이 존재한다. 그에 반해, RBSN 모델은 경계면을 통해 균열을 모사함으로써 균열이 발생한 경계면의 방향성 고려를 통해 이방성의 투수계수를 반영할 수 있어 균열의 진행 방향을 조금 더 명확하게 도출할 수 있다는 장점이 있다. 다만, Kim et al.(2021)은 매질을 취성 파괴 물질로 가정하고 Mohr-Coulomb 파괴 규준에 따라 매질의 파괴 계수를 0 또는 1로만 고려하여 손상 또는 미손상 영역의 수리-역학적 물성 변화를 고려했다는 한계점이 존재한다. 이를 앞서 언급한 Tang et al.(2002)의 손상 모델과 연계하여 파괴 계수를 도출한다면 좀 더 실제와 가까운 해석 결과를 얻을 수 있을 것이라고 판단된다.

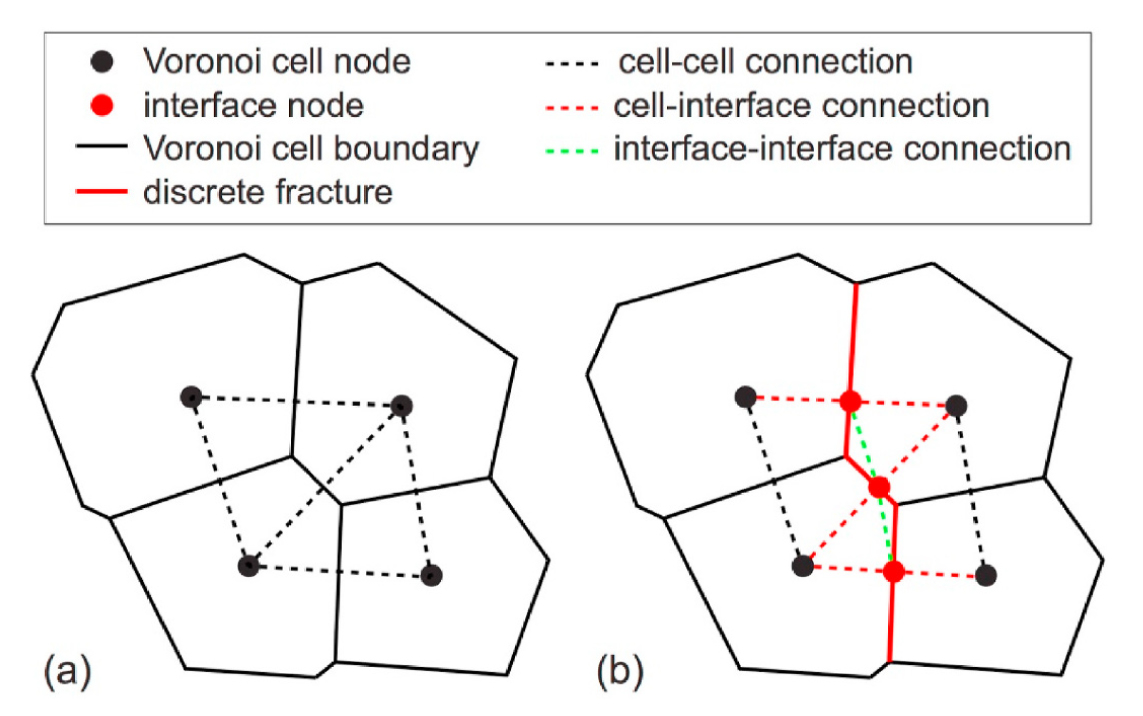
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F10.jpg

Fig. 10

TOUGH-RBSN concept of dilatant flow path creation as a result of reactivation of weak interfaces between porous aggregates: (a) before reactivation and (b) after reactivation of interfaces and creation of discrete fracture or flow path (Kim et al., 2021).

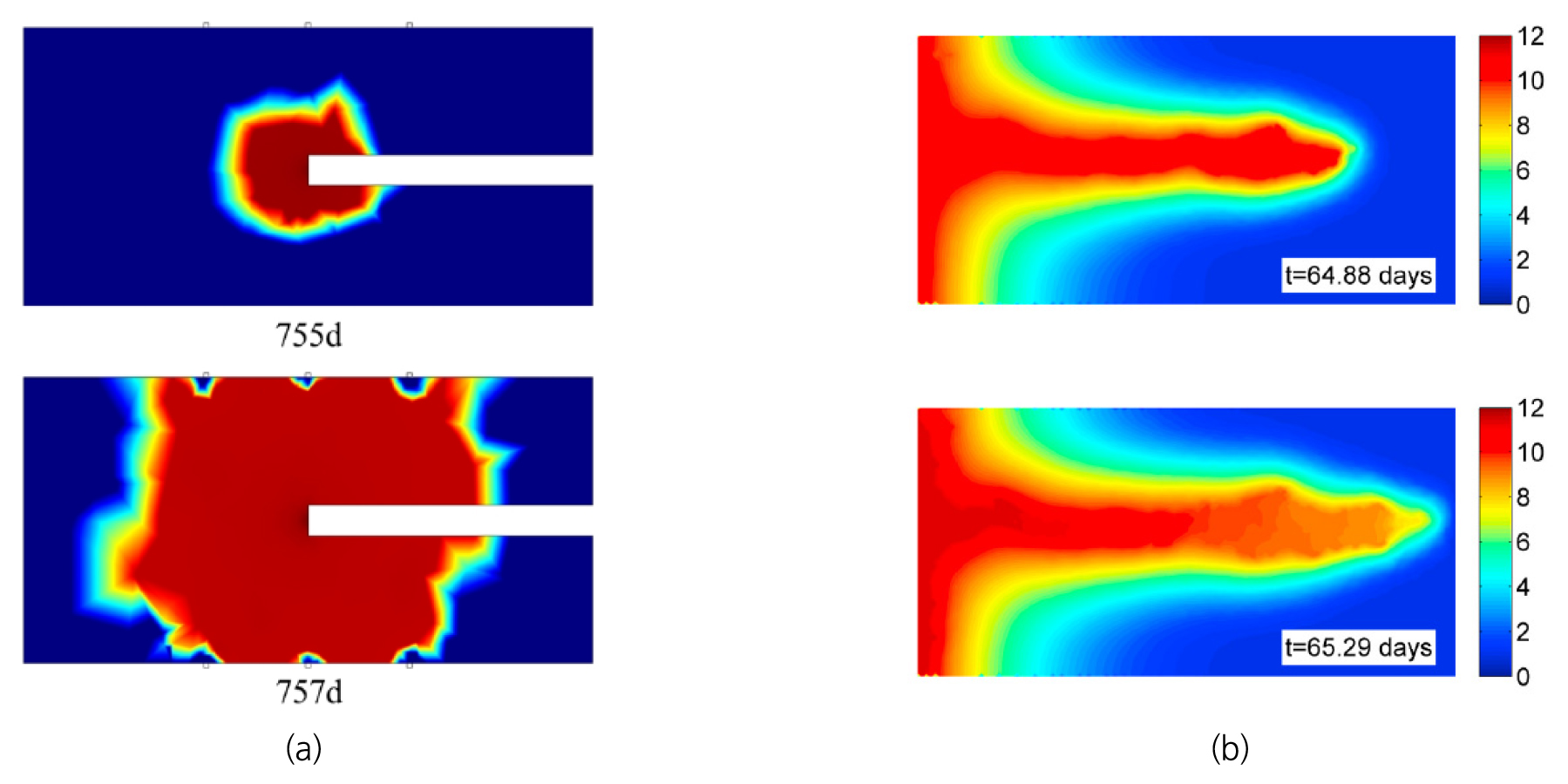
https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310502/images/ksrm_31_05_02_F11.jpg

Fig. 11

Fracturing and propagation of dilatant flow paths: (a) continuum damage model(Lee et al., 2020e), (b) discrete rigid-body-spring network model (Kim et al., 2021)

3.2.2 수리 모델(hydraulic model)

기체 이동성 규명을 위한 수리학적 모델은 대부분의 수치 모델에서 Darcy의 법칙을 적용하여 해석을 수행하였다. 포화 벤토나이트 내 기체 이동 모사를 위해서는 균열 발생 이전의 공극 구조 변화에 의한 고유 투수계수 변화와 균열 발생으로 이후의 고유 투수계수 변화를 모두 반영할 수 있어야 한다. 이처럼 고유 투수계수의 변화는 매질의 역학적 변화의 함수로서 공극률, 체적 변형률, 인장 변형률, 소성 변형률, 그리고 파괴 변수의 함수로 나타낼 수 있다. 기존 연구에서 적용한 고유 투수계수 모델은 Table 4와 같이 네 가지 유형 (i) 공극률 기반 모델(porosity-based model)(Tamayo-Mas and Harrington, 2020), (ii) 변형률 기반 모델(strain-based model)(Nguyen and Le, 2015), (iii) 손상 기반 모델(damage-based model)(Kawai, 1978, Meschke and Grasberger, 2003, Fall et al., 2014, Dagher et al., 2019), 그리고 (iv) 균열 내재 모델(embedded fracture model, EFM)(Olivella and Alonso, 2008)이 있다.

Table 4.

Models for intrinsic permeability for gas migration in barrier materials (modified Table 2 in Guo and Fall, 2021)

Model categories	Models for intrinsic permeability	Eq.	References
Porosity-based	$k = k_{0} \exp [C_{1} ϕ - ϕ_{0}]$	(10)	Modified from Davies and Davies, 2001, Rutqvist and Tsang, 2002
Strain-based	$k = k_{0} \exp (C_{2} ε_{v} + C_{3} \bar{ε_{p l}})$	(11)	Nguyen and Le, 2015
Damage-based	$k_{U D} = k_{0} \frac{ϕ_{0}^{3}}{(1 - ϕ_{0})^{2}} \frac{(1 - ϕ)^{2}}{ϕ^{3}}$ $k_{D} = k_{0} + \frac{b^{3}}{12 a}$	(12) (13)	Kawai, 1978
Damage-based	$k = k_{U D} + k_{D}$ $k_{U D} = k_{0} \exp [C_{4} (ϕ - ϕ_{0})]$ $k_{D} = \frac{D}{D_{m a x}} (k_{m a x} - k_{U D})$	(14) (15) (16)	Meschke and Grasberger, 2003, Fall et al., 2014, Dagher et al., 2019
Embedded fracture	$k = k_{m a t} I + \frac{b^{3}}{12 a} n_{f} \otimes n_{f}$ $b = b_{0} + a < ε_{n} - ε_{0} >$	(17) (18)	Olivella and Alonso, 2008

Note: k is the intrinsic permeability, C_i is the empirical parameter for calibration, Ø is the porosity, ε_v is the volumetric strain, $\bar{ε_{p l}}$ is the equivalent plastic strain, k_UD is the undamaged permeability, k_D is the damaged permeability, b is the aperture, a is the fracture spacing, D is the damage variable, D _max is the maximum damage variable, k _max is the maximum permeability corresponding to D _max, k _mat is the permeability of clay matrix, n_f is the normal vector of fracture, and subscript ₀ represents the initial state

공극률 기반 모델과 변형률 기반 모델은 다른 유형들에 비해 모델이 상대적으로 간편하다는 장점이 있지만, 균열 발생 이후 균열을 통한 팽창 흐름이 주를 이루는 매질의 수리학적 특성을 제대로 반영하기는 어렵다는 단점이 있다. 이를 보완하기 위한 방안으로 Meschke and Grasberger(2003)이 제안한 파괴 계수를 적용하여 손상 영역과 미계수의 영향을 반영할 수 있는 손상 기반 모델들이 주를 이루고 있다(Fall et al., 2014, Dagher et al., 2019).

또한, Olivella and Alonso(2008)은 수리 해석에서 요소의 크기가 요소의 투수계수에 미치는 영향은 크지 않으며, 요소의 투수계수는 균열의 폭에 더 크게 영향을 받는다고 주장하였다. 또한, 균열의 수직 방향 투수계수는 균열 발생 이전의 고유 투수계수와 같다고 서술하였다. 이러한 연구 결과를 반영하여 최근에는 EFM과 같은 다양한 균열 특성(균열의 틈, 간격, 방향 등)을 고려할 수 있는 고유 투수계수 모델의 적용에 대한 관심이 증가되고 있다(Olivella and Alonso, 2008, Kim et al., 2021).

상대 투수율(relative permeability) 모델

다양한 접근 방법이 제시된 고유 투수계수 모델과는 달리, 팽창 흐름으로 인한 불포화 상태의 다상 유동 흐름 모사를 위한 물과 가스의 상대 투수율 모델은 대부분의 문헌에서 Mualem-van Genuchten 모델(Xu et al., 2013, Ye et al., 2014, Sedighi et al., 2015, Dagher et al., 2019) 또는 power law 모델(Olivella and Alonso, 2008, Gerard et al., 2014, Damians et al., 2017)을 주로 사용하였다(Table 5). 이는 DECOVALEX-2019 Task A에서도 마찬가지였으며, 적용된 상대 투수율에 따른 해석 모델의 예측치에는 큰 영향이 없는 것을 확인하였다. 또한, 실제의 상대 투수율은 포화도뿐만 아니라 포화 이력(saturation history)에도 영향을 받는다(Juanes et al., 2006). 포화 과정에서 일부 기체는 공극 속에 갇혀 공극 내 흡수력을 발생시킬 수 있고 이는 포화 또는 건조 과정에 따라 수분 보유 곡선의 차이를 발생시킨다. 이론상으로 상대 투수율은 포화도에 따른 공극 내 흡수력의 관계인 수분 보유 곡선에 크게 영향을 받는다. 이러한 영향을 고려하기 위해 선행 연구에서 다양한 방법으로 포화 이력을 고려한 상대 투수율 모델을 제안하였지만(Land, 1968, Killough, 1976, Juanes et al., 2006), Guo and Fall(2018)은 포화 이력을 고려한 상대 투수율 모델을 적용한 해석 결과는 기존의 유효 포화도만을 고려한 상대 투수율 모델을 적용한 결과와 점토 매질 내 기체의 이동 모사에는 큰 차이가 없는 것을 확인하였다. 따라서, 점토 내 기체의 이동성 모사 시에는 모델의 간결성과 해석 시간을 고려했을 때 유효 포화도만을 고려한 모델을 사용하는 것이 합리적이라고 판단된다.

Table 5.

Models for relative permeability for gas migration in barrier materials

Categories	Model for relative permeability	Eq.	References
Mualem-van Genuchtem model (MGM)	$k_{r w} (S_{e}) = \sqrt{S_{e}} [1 - (1 - S_{e}^{1 / m})^{m}]^{2}$ $k_{r g} (S_{e}) = \sqrt{1 - S_{e}} (1 - S_{e}^{1 / m})^{2 m}$	(19) (20)	Fredlund et al., 1994, Mualem, 1976, van Genuchten, 1980
Power law model (PLM)	$k_{r α} (S_{e α}) = S_{e α}^{n_{α}}$	(21)	Mualem, 1978

Note: k_rw and k_rg are relative permeability of water and gas, S_e is the effective saturation, m is a fitting parameter, subscript α represents fluid component α, and n_α is a parameter depending on soil type.

3.3 전산 모사 해석 연구 동향 소결

3.3.1 기체 이동 모사 전산 모델 개발

현재까지 점토 매질 내 기체 이동 모사를 위한 다양한 수치 모델들이 제안되어왔다. 2절에서 언급한 바와 같이 실내 및 현장 실험 사례들로부터 상대적으로 낮은 투수성을 가진 점토 매질 내의 기체 이동 현상은 투수성이 높은 사질토 내 기체 이동 거동과는 다른 특성들이 나타나는 것을 확인할 수 있었다. 앞선 실험적 연구 사례들에서 관측된 현상들을 바탕으로 점토 매질 내 기체 이동 메커니즘 규명을 위한 전산 모델 개발 시 필수적으로 고려되어야 할 특성들은 다음과 같다.

- 포화도 변화에 따른 점토 매질의 팽윤 특성

- 팽윤압에 의한 균열의 생성/폐쇄 현상과 이로 인한 균열의 전파 특성

- 팽윤압 또는 공극 압력에 따른 매질의 손상 영향 특성

- 손상도에 따른 매질 내 고유 투수계수 변화 특성

- 균열 발생 시 팽창 흐름으로 인한 다상 유동 특성

문헌 연구를 바탕으로 위와 같은 특징을 반영할 수 있는 점토 물질 내 기체 이동 메커니즘 규명 전산 모델 개발 시 세부 모델 선정 절차를 Table 6와 같이 정리하였다. 모델 선정 절차는 역학 모델 선정을 최우선으로 결정하는 것을 제안하였다. 역학 모델 선정 시 가장 중요한 요인은 해석 대상 매질의 초기 포화 상태이다. 앞서 서술한 바와 같이 초기 포화 상태의 점토 매질 내 기체 유입 또는 생성으로 인한 불포화 특성(흡입력 변화, 팽윤 거동 등)의 영향은 크지 않기 때문에 초기 포화 상태에 따라 상대적으로 간단한 탄성 역학 모델의 선택이 가능하고 이를 통해 해석 시간을 줄일 수 있다. 다만, 불포화 해석의 경우 탄소성 모델인 MCCM 또는 열탄소성 모델인 BBM을 적용하여 추가적인 팽윤 특성 모델을 적용시키지 않아도 되는 선택이 합리적이라고 판단된다.

Table 6.

Model selection chart for gas migration in clay material

Model	Saturated condition	Unsaturated condition	Note
Mechanical constitutive	Elasticity (Linear/nonlinear)	Elasto-plastic (Modified cam clay model, MCCM) Thermo-elasto-plastic (Barcelona basic model, BBM)	Determined according to the target interpretation period and reliability
Swelling	$ε_{s w} = f (S_{l}, C_{i})$ or $P_{s w} = f (S_{l}, C_{i})$	Embedded	Additional nonlinear model has to be developed
Damage	$E = f (E_{0}, D)$		Recommend to be coupled with fracture model
Fracturing	Continuum model (Cohesive zone model, CZM) Discrete model (Rigid-body-spring-network, RBSN)		Determined according to the numerical method Self-healing mechanism has to be considered
Hydro- Mechanical	$k_{m a t} = f (k_{U D}, k_{D})$		-
Intrinsic permeability	$k_{U D} = f (ϕ, k_{0})$ $k_{D} = f (ϕ, k_{0}, D, s, a)$		Additional fracture parameters (e.g., aperture, space) have to be considered
Relative permeability	$k_{r} = f (k_{0}, S_{e}, C_{i})$		-

Note: ε_sw is the volumetric strain due to the swelling, P_sw is the swelling pressure, S_l is the saturation, E is the elastic modulus, E₀ is the initial elastic modulus, D is a damage variable, k_mat is the permeability of matrix, k_UD is the undamaged permeability, k_D is the damaged permeability, Ø is the porosity, k0 is the intrinsic permeability, s is the fracture spacing, a is the aperture, k_r is the relative permeability, S_e is the effective saturation, and C_i is the fitting parameter for calibration.

탄성, 탄소성, 열탄소성 모델에 관계 없이 매질 손상에 따른 수리학적 특성 변화 고려를 위한 손상도 모델을 적용해야 한다. 추가로 손상도 모델만으로는 균열의 방향성 모사가 어렵기 때문에 균열 전파 모델을 필수적으로 적용해야 한다. 균열 전파 모델은 전산 해석 시 요소를 연속체로 고려하는지 불연속체로 고려하는지에 따라 CZM 또는 RBSN 모델을 선정할 수 있다. 다만, 불연속 해석을 활용하는 RBSN 모델이 조금 더 실제에 가까운 균열 전파 모사가 가능하다.

또한, 손상에 의한 매질의 수리학적 변화 고려를 위해 응력-변형률 관계에 따른 매질의 고유 투수계수 변화 모델과 균열 발생 이후의 팽창 흐름으로 인한 다상 유동 흐름 해석을 위한 상대 투수율 모델을 적용하여 해석을 수행해야 한다. 문헌 연구로부터 고유 투수계수 모델 또는 상대 투수율 모델의 선정에 따른 해석 결과의 차이는 크지 않음을 확인하였다. 다만, 균열의 발생과 전파로 인한 고유 투수계수 모델 선정 시 균열의 틈, 간격을 고려할 수 있는 모델을 선정한다면 조금 더 실제에 가까운 모사가 가능하다고 판단된다.

추가로 점토 매질 내 기체의 이동 및 우선 경로의 발달은 복잡한 비선형성 특징을 나타내는 수리-역학적 복합거동 현상으로 좀 더 신뢰도 높게 우선 경로의 발달을 모사하기 위해서는 명시적 방법(explicit method)을 적용한 수치 해석이 수행되어야 한다. 다만 현재까지 명시적 방법을 통한 수치 해석적 연구가 거의 수행되지 않았다. 몇몇 연구자들에 의해 위상 필드 방법(phase field method), XFEM, 그리고 TOUGH-UDEC 모델 등의 접근법이 시도된 바 있지만, 기체 주입 시험 전산 모사의 신뢰도 높이기 위해서는 추가적인 수치 모델들이 지속적으로 개발되어 상호 검증되어야 한다.

3.3.2 DECOVALEX-2023 소개 및 추후 연구 제안

이 절에서는 점토 물질 내 기체 이동 전산 모사 모델의 신뢰도 향상 및 기체 이동 메커니즘 규명을 위한 추후 연구 내용 소개의 일환으로 DECOVALEX-2023 Task B의 연구 목표 및 내용을 공유하고자 한다. 현재 진행되고 있는 DECOVALEX-2023 Task B에서는 기존 DECOVALEX-2019 Task A에서 수행된 1차원/ 3차원 기체 주입 실험 모사 전산 모델 개발 연구를 바탕으로, 개발된 모델의 신뢰도 향상 연구에 집중하고 있다. 특히, DECOVALEX-2019 Task A를 통해 제안된 전산 모델을 이용하여 실험 결과를 검증할 경우 보정 계수의 적용에 따라 그 결과에는 현저한 차이가 발생하였다. 또한, 각 모델에 따라 적용해야 하는 보정 계수의 수가 많고 인장 강도, 팽윤 압력과 같은 보정 매개변수를 제외하고는 명확한 물리적 의미를 갖지 않는 경우가 많았다. 따라서, 향후 연구에서는 실험에서 나타난 확률적 물리 현상들에 대한 심도 있는 고찰이 필요하며 이를 반영할 수 있는 보정 매개변수 선정에 대한 연구가 필요하다.

또한, DECOVALEX-2019에서 제안된 전산 모델 중 CNSC-PD, UPC/Andra-ED를 제외하고 포화 벤토나이트의 이질성(heterogeneity)을 고려한 모델이 전무하였다. 실제 실험에 사용된 시료 또는 실제 심층처분시스템의 완충재는 필연적으로 이질성을 가지며, 이로 인한 기체 이동성은 확률적 거동을 하게 된다. 이러한 확률적 거동 예측성 향상을 위해 전산 모델에서는 매질의 이질성을 반영할 수 있도록 모델을 수정 보완해야 한다.

마지막으로 DECOVALEX-2023에서는 연구실 규모의 실험 데이터를 활용한 모델 검증뿐만 아니라 실규모 실험 데이터를 활용한 검증을 목표로 연구를 수행하고 있다. 실규모 검증을 위한 전산 해석은 연구실 규모 실험 해석보다 더 많은 컴퓨팅 메모리를 필요로 하는 작업이다. 따라서, 최소한의 요소망과 비선형 거동을 하는 변수를 최대한 줄여 최소한의 해석 시간에도 적정한 예측 신뢰도를 확보할 수 있는 전산 모델 개발 연구를 지속해야 한다.

4. 결 언

고준위방사성폐기물 처분시스템에서 예상되는 기체 발생으로 인한 점토 물질 기반 완충재의 수리-역학적 복합거동의 특성 파악 및 예측을 위해 세계 각국에서 실험실 규모부터 실대형 규모까지 다양한 실험과 수치모델링 기법 개발 연구가 수행되어왔으며, 최근에는 해당 분야의 전문가들이 모여 DECOVALEX와 같은 국제공동연구를 진행함으로써 연구 수준의 향상을 위해 노력하고 있다. 정기적인 학술 교류를 통해 각 기관에서 개발 중인 모델링 기법 적용 결과들을 비교 및 검증하고 개발 과정에서의 경험을 공유하고 있으며, 학술적 토론을 거쳐 각 모델링 기법의 문제점을 보완해나감으로써 모델의 정확성과 신뢰성을 향상시키고 있다. DECOVALEX-2019에서는 영국 지질조사소에서 수행한 실험실 규모의 기체 주입 시험으로부터 획득한 자료를 기반으로 점토 물질에서의 기체 이동 거동 특성을 파악하고, 수리-역학적 복합거동을 모사하기 위한 수치모델링 기법을 제안하였고, 더 나아가 DECOVALEX-2023 스웨덴 Äspö 지하처분연구시설에서 수행된 실규모 현장 실험 자료를 기반으로 처분장 실제 규모를 반영할 수 있는 해석 기법으로 단계적으로 확장을 통해 기술적 발전이 이루어지고 있다.

국내의 경우, 한국원자력연구원이 DECOVALEX-2019의 Task A에 참여하여 역학 손상 모델 및 손상도를 고려한 2상 유동 모델을 개발하였고, 실내 기체 주입 시험 결과를 모사함으로써 모델의 적용성을 검증하였다. 한국원자력연구원이 2008년도부터 DECOVALEX-2011에 참여하기 시작하여 공학적방벽 및 기체에서의 열-수리-역학적 복합거동 모델링 연구를 지속적으로 수행해오면서 연구적 수준을 향상시켜왔고, 국내 환경에 적합한 각종 시험을 수행하여 획득한 기초 자료를 기반으로 독자적 해석 모델을 구축한 반면에, 점토 물질에서의 기체 이동 관련 연구는 초기 단계 수준이다. 국내 처분 환경에 적합한 벤토나이트 시료를 활용한 실험실 규모의 실내 기체 주입 시험을 통해 기초 자료를 확보할 필요가 있으며, 이를 기반으로 해석 모델을 정립한 후 더 나아가 추후 공학적 규모 실험을 수행하고 해석 기법을 확장할 필요가 있다고 판단된다.

국내 처분 환경에 적합한 벤토나이트 시료에서의 전주기적 기체 이동 현상에 대한 거동 특성을 파악하기 위해 실내 기체 주입 시험 장치를 자체적으로 개발하여 초기 기체 주입 단계, 기체 유입 단계, 기체 돌파 발생 단계, 기체 주입 중단 이후의 단계 등 여러 단계에 걸쳐 기체 주입 압력, 기체 유입 및 유출 속도, 공극압, 응력을 계측함으로써 기체 이동의 단계별 거동 특성을 파악하는 연구를 수행할 필요가 있으며, 공학적방벽 벤토나이트 완충재에서의 기체 이동 현상을 모사하기 위한 모델 개발 및 검증 연구를 지속적으로 수행함으로써 향후 국내 처분 환경에 적합한 벤토나이트를 활용한 실험을 통해 획득한 자료를 기반으로 기체 이동을 적절히 모사할 수 있는 모델을 확보할 필요가 있다.

Acknowledgements

이 논문은 2021년도 정부(과학기술정보통신부)의 재원으로 사용후핵연료관리핵심기술개발사업단 및 한국연구재단의 지원(2021M2E1A1085193)과 고준위폐기물관리차세대혁신기술개발사업의 지원(2021M2E3A2041312)을 받아 수행된 연구사업입니다.글

References

Ando, K., Adachi, T., Fujiwara, A., Vomvoris, S., Marshall, P., Lanyon, B., Yamamoto, S., Shimmura, A., 2002, The in-situ gas migration test (GMT) at the Grimsel test site: resaturation phase of silo type repository, Clays In Natural And Engineered Barriers For Radioactive Waste Confinement, December 9-12, 2002, Reims, France.

Alonso, E. E., Gens, A., Josa, A, 1990, A constitutive model for partially saturated soils, Géotechnique, Vol. 40(3), pp. 405-430. 10.1680/geot.1990.40.3.405

Bond, A., Chittenden, N., Thatcher, K., 2018, RWM Coupled Processes Project: First Annual Report for DECOVALEX-2019, Quintessa Report to RWM. QRS-1612D-R1 v1.2. Quintessa Ltd., Henley-on-Thames, UK.

Cuss, R.J., Harrington, J.F., Giot, R., Auvray, C., 2014a, Experimental observations of mechanical dilation at the onset of gas flow in Callovo-Oxfordian claystone, In: Norris, S., Bruno, J., (eds) Clays in Natural and Engineered Barriers for Radioactive Waste Confinement, Geological Society, London, Special Publications, Vol. 400, pp. 507-519. 10.1144/SP400.26

Cuss, R.J., Harrington, J.F., Noy, D.J., 2012, Final Report of FORGE WP4.1.1: The stress path permeameter experiment conducted on Callovo-Oxfordian Claystone, British Geological Survey Commissioned Report, CR/12/140. 116pp. British Geological Survey, Keyworth, Nottingham, UK.

Cuss, R.J., Harrington, J.F., Noy, D.J., Graham, C.C., Sellin, P., 2014b, Evidence of localised gas propagation pathways in a field-scale bentonite engineered barrier system; results from three gas injection tests in the large scale gas injection test (Lasgit), Applied Clay Science, Vol. 102, pp. 81-92. 10.1016/j.clay.2014.10.014

Cuss, R.J., Harrington, J.F., Noy, D.J., Wikman, A., Sellin, P., 2011, Large scale gas injection test (Lasgit): Results from two gas injection tests, Physics and Chemistry of the Earth, Vol. 36, pp. 1729-1742. 10.1016/j.pce.2011.07.022

Dagher, E.E., Nguyen, T.S., Sedano, J.I., 2019, Development of a mathematical model for gas migration (two-phase flow) in natural and engineered barriers for radioactive waste disposal, Geological Society, London, Special Publications, Vol 482(1), pp. 115-148. 10.1144/SP482.14

Damians, I.P., Olivella, S., Gens, A., 2017, Modelling gas flow experiments in Mx80 bentonite, In 9th Workshop on CODE_BRIGHT, Barcelona.

Davies, J.P., Davies, D.K., 2001, Stress-dependent permeability: characterization and modeling, Spe Journal, Vol. 6(2), pp. 224-235. 10.2118/71750-PA

Donohew, A.T,, Horseman, S.T., Harrington, J.F., 2000, Gas entry into unconfined clay pastes at water contents between the liquid and plastic limits, pp. 369-394 in: Environmental Mineralogy-Microbial Interactions, Anthropogenic Influences, Contaminated Land and Waste Management (J.D. Cotter-Howells, L.S. Campbell, E. Valsami-Jones, M. Batchelder, editors), Mineralogical Society Special Publication, 9. Mineralogical Society of Great Britain and Ireland, London, UK. 10.1180/MSS.9.18

Fall, M., Nasir, O., Nguyen, T.S., 2014, A coupled hydro-mechanical model for simulation of gas migration in host sedimentary rocks for nuclear waste repositories, Engineering Geology, Vol. 176, pp. 24-44. 10.1016/j.enggeo.2014.04.003

Fredlund, D.G., Xing, A., Huang, S., 1994, Predicting the permeability function for unsaturated soils using the soil-water characteristic curve, Canadian Geotechnical Journal, Vol. 31(4), pp. 533-546. 10.1139/t94-062

Gallé, C., 1998, Migration des gaz et pression de rupture dans une argile compactée destinée à la barrière ouvragée d'un stockage profound, Bulletin de la Société Géologique de France, Vol. 169, pp. 675-680.

Gallé, C., 2000, Gas breakthrough pressure in compacted Fo-Ca clay and interfacial gas overpressure in waste disposal context, Applied Clay Science, Vol. 17, pp. 85-97. 10.1016/S0169-1317(00)00007-7

Gallé, C., Tanai, K., 1998, Evaluation of gas transport properties of backfill materials for waste disposal: H2 migration experiments in compacted Fo-Ca Clay, Clays and Clay Minerals, Vol. 46, pp. 498-508. 10.1346/CCMN.1998.0460503

Gens, A., 1995, Constitutive laws, In Modern issues in non-saturated soils, pp. 129-158, Springer, Vienna. 10.1007/978-3-7091-2692-9_2

Gerard, P., Harrington, J., Charlier, R., Collin, F., 2014, Modelling of localised gas preferential pathways in claystone, International Journal of Rock Mechanics and Mining Sciences, Vol. 67, pp. 104-114. 10.1016/j.ijrmms.2014.01.009

Graham, J., Halayko, K.G., Hume, H., Kirkham, T., Gray, M., Oscarson, D., 2002, A capilliarity-advective model for gas break-through in clays, Engineering Geology, Vol. 64, pp. 273-286. 10.1016/S0013-7952(01)00106-5

Graham, C.C., Harrington, J.F., 2014, Final Report of FORGE 3.2.1: Key Gas Migration Processes in Compact Bentonite, FORGE Report D3.33. British Geological Survey, Keyworth, Nottingham, UK.

Graham, C.C., Harrington, J.F., Cuss, R.J., Sellin, P., 2012, Gas migration experiments in bentonite: implications for numerical modelling, Mineralogical Magazine, Vol. 76(8), pp. 3279-3292. 10.1180/minmag.2012.076.8.41

Guo, G., Fall, M., 2018, Modelling of dilatancy-controlled gas flow in saturated bentonite with double porosity and double effective stress concepts, Engineering Geology, Vol. 243, pp. 253-271. 10.1016/j.enggeo.2018.07.002

Guo, G., Fall, M., 2021, Advances in modelling of hydro-mechanical processes in gas migration within saturated bentonite: A state-of-art review, Engineering Geology, 106123. 10.1016/j.enggeo.2021.106123

Hallett, P.D., Newson, T.A., 2005, Describing soil crack formation using elastic-plastic fracture mechanics, European Journal of Soil Science, Vol. 56(1), pp. 31-38. 10.1111/j.1365-2389.2004.00652.x

Harrington, J.F., 2016, Task A: Stage 1A: 1D flow through saturated bentonite under constant volume boundary conditions, British Geological Survey, Pers. comm. 05/10/2016.

Harrington, J.F., De Lavaissière, R., Noy, D.J., Cuss, R.J., Talandier, J., 2012, Gas flow in Callovo-Oxfordian claystone (COx): results from laboratory and field-scale measurements, Mineralogical Magazine, Vol. 76, pp. 3303-3318. 10.1180/minmag.2012.076.8.43

Harrington, J.F., Graham, C.C., Cuss, R.J., Norris, S., 2017, Gas network development in a precompacted bentonite experiment: Evidence of generation and evolution, Applied Clay Science, Vol. 147, pp. 80-89. 10.1016/j.clay.2017.07.005

Harrington, J.F., Horseman, S.T., 2003, Gas Migration in KBS-3 Buffer Bentonite: Sensitivity of Test Parameters to Experimental Boundary Conditions, SKB Technical Report No. TR-03-02. Svensk Kärnbränslehantering AB, Stockholm, Sweden.

Harrington, J.F., Horseman, S.T., 1999, Gas transport properties of clays and mudrocks, In: Aplin, A.C., Fleet, A.J., Macquaker, J.H., (eds) Muds and Mudstones: Physical and Fluid Flow Properties, Geological Society of London, London, Special Publications, Vol. 158, pp. 107-124.Harrington, J.F., Horseman, S.T., 2003, Gas Migration in KBS-3 Buffer Bentonite: Sensitivity of Test Parameters to Experimental Boundary Conditions, SKB Technical Report No. TR-03-02. Svensk Kärnbränslehantering AB, Stockholm, Sweden. 10.1144/GSL.SP.1999.158.01.09

Hoch, A.R., Cliffe, K.A., Swift, B.T., Rodwell, W.R., 2004, Modelling Gas Migrationin Compacted Bentonite: GAMBIT Club Phase 3, Final Report, POSIVA, Olkiluoto, Finland.

Horseman, S.T., Harrington, J.F., Sellin, P., 1996, Gas Migration in MX80 Buffer Bentonite, In: Symposium on the Scientific Basis for Nuclear Waste Management XX (Boston), Materials Research Society, 465, pp. 1003-1010. 10.1557/PROC-465-1003

Horseman, S.T., Harrington, J.F., Sellin, P., 1999, Gas migration in clay barriers, Engineering Geology, Vol. 54, pp. 139-149. 10.1016/S0013-7952(99)00069-1

Horseman, S.T., Harrington, J.F., Sellin, P., 2003, Water and gas movement in Mx80 bentonite buffer clay, MRS Online Proceedings Library (OPL), pp. 807. 10.1557/PROC-807-715

Horseman, S.T., Harrington, J.F., Sellin, P., 2004, Water and Gas Movement in Mx80 Bentonite Buffer Clay, In: Symposium on the Scientific Basis for Nuclear Waste Management XXVII (Kalmar), Materials Research Society, Vol. 807, pp. 715-720. 10.1557/PROC-807-715

Juanes, R., Spiteri, E.J., Orr Jr, F.M., Blunt, M.J., 2006, Impact of relative permeability hysteresis on geological CO2 storage, Water resources research, Vol. 42(12). 10.1029/2005WR004806

KACHANOV, L.M., 1958, Time of the rupture process under creep conditions, Izy Akad. Nank SSR Otd Tech Nauk, Vol. 8, pp. 26-31.

Kawai, T., 1978, New discrete models and their application to seismic response analysis of structures, Nuclear engineering and design, Vol. 48(1), pp. 207-229. 10.1016/0029-5493(78)90217-0

Killough, J.E., 1976, Reservoir simulation with history-dependent saturation functions, Society of Petroleum Engineers Journal, Vol. 16(1), pp. 37-48. 10.2118/5106-PA

Kim, K., Rutqvist, J., Harrington, J.F., Tamayo-Mas, E., Birkholzer, J.T., 2021, Discrete dilatant pathway modeling of gas migration through compacted bentonite clay, International Journal of Rock Mechanics and Mining Sciences, Vol. 137, pp. 104569. 10.1016/j.ijrmms.2020.104569

Land, C.S., 1968, Calculation of imbibition relative permeability for two-and three-phase flow from rock properties, Society of Petroleum Engineers Journal, Vol. 8(2), pp. 149-156. 10.2118/1942-PA

Lee, C., Choi, H.J., Kim, G.Y., 2020a, Numerical modeling of coupled thermo-hydro-mechanical behavior of mx80 bentonite pellets, Tunnel and Underground Space, Vol. 30(5), pp. 446-461.

Lee, C., Lee, J., Kim, G.Y., 2020b, Numerical analysis of FEBEX at Grimsel Test Site in Switzerland, Tunnel and Underground Space, Vol 30(4), pp. 359-381.

Lee, C., Lee, J., Kim, M., Kim, G.Y., 2020c, Implementation of Barcelona Basic Model into TOUGH2-MP/FLAC3D, Tunnel and Underground Space, Vol. 30(1), pp. 39-62.

Lee, C., Yoon, S., Lee, J., Kim, G.Y., 2019, Introduction of Barcelona Basic Model for Analysis of the Thermo-Elasto-Plastic Behavior of Unsaturated Soils, Tunnel and Underground Space, Vol. 29(1), pp. 38-51.

Lee, J., Kim, I., Ju, H., Choi, H., Cho, D., 2020d, Proposal of an Improved Concept Design for the Deep Geological Disposal System of Spent Nuclear Fuel in Korea, Journal of Nuclear Fuel Cycle and Waste Technology, Vol. 18(S), pp. 1-19. 10.7733/jnfcwt.2020.18.S.1

Lee, J., Lee, C., Kim, G.Y., 2020e, Numerical Modelling for the Dilation Flow of Gas in a Bentonite Buffer Material: DECOVALEX-2019 Task A, Tunnel and Underground Space, Vol. 30(3), pp. 382-393.

Lee, J., Lee, C., Kim, G.Y., 2020f, Numerical Modelling of One Dimensional Gas Injection Experiment using Mechanical Damage Model: DECOVALEX-2019 Task A Stage 1A, Tunnel and Underground Space, Vol. 29(4), pp. 262-279.

Marschall, P., Horseman, S.T., Gimmi, T., 2005, Characterisation of gas transport properties of the opalinus clay, a potential host rock formation for radioactive waste disposal, Oil and Gas Science and Technology - Rev. IFP, Vol. 60, pp. 121-139. 10.2516/ogst:2005008

Mazars, J., 1984, Application de la mécanique de l'endommagement au comportement non linéaire et à la rupture du béton de structure, THESE DE DOCTEUR ES SCIENCES PRESENTEE A L'UNIVERSITE PIERRE ET MARIE CURIE-PARIS 6.

Mazars, J., 1986, A description of micro-and macroscale damage of concrete structures, Engineering Fracture Mechanics, Vol. 25(5-6), pp. 729-737. 10.1016/0013-7944(86)90036-6

Mazars, J., Pijaudier-Cabot, G., 1989, Continuum damage theory-application to concrete, Journal of engineering mechanics, Vol. 115(2), pp. 345-365. 10.1061/(ASCE)0733-9399(1989)115:2(345)

Meschke, G., Grasberger, S., 2003, Numerical modeling of coupled hydromechanical degradation of cementitious materials, Journal of engineering mechanics, Vol. 129(4), pp. 383-392. 10.1061/(ASCE)0733-9399(2003)129:4(383)

Mualem, Y., 1976, A new model for predicting the hydraulic conductivity of unsaturated porous media, Water resources research, Vol. 12(3), pp. 513-522. 10.1029/WR012i003p00513

Mualem, Y., 1978, Hydraulic conductivity of unsaturated porous media: generalized macroscopic approach, Water Resources Research, Vol. 14(2), pp. 325-334. 10.1029/WR014i002p00325

Nash, P.J., Swift, B.T., Goodfield, M., Rodwell, W.R., 1998, Modelling gas migration in compacted bentonite, Posiva Report, pp. 98-08.

Nguyen, T.S., Le, A.D., 2015, Simultaneous gas and water flow in a damage-susceptible bedded argillaceous rock, Canadian Geotechnical Journal, Vol. 52(1), pp. 18-32. 10.1139/cgj-2013-0457

Olivella, S., Alonso, E.E., 2008, Gas flow through clay barriers, Géotechnique, Vol. 58(3), pp. 157-176. 10.1680/geot.2008.58.3.157

Pusch, R., Forsberg, T., 1983, Gas Migration through Bentonite Clay, SKB Technical Report 83-71, Svensk Kärnbränslehantering AB, Stockholm, Sweden.

Pusch, R., Ranhagen, L., Nilsson, K., 1985, Gas Migration through MX-80 Bentonite, Nagra Technical Report NTB 85-36, Nagra, Wettingen, Switzerland.

Rutqvist, J., Tsang, C.F. (2002). A study of caprock hydromechanical changes associated with CO 2-injection into a brine formation. Environmental Geology, 42(2-3), 296-305. 10.1007/s00254-001-0499-2

Rutqvist, J., Ijiri, Y., Yamamoto, H. (2011). Implementation of the Barcelona Basic Model into TOUGH-FLAC for simulations of the geomechanical behavior of unsaturated soils. Computers & Geosciences, 37(6), 751-762. 10.1016/j.cageo.2010.10.011

Rutqvist, J., Kim, K., Xu, H., Guglielmi, Y., Birkholzer, J. (2018). Investigation of Couple d Processes in Argillite Rock: FY18 Progress. Prepared for US Department of Energy. Spent Fuel and Waste Disposition. LBNL, 2001168. 10.2172/1462005PMC5904710

Sedighi, M., Thomas, H.R., Al Masum, S., Vardon, P.J., Nicholson, D., Chen, Q. (2015). Geochemical modelling of hydrogen gas migration in an unsaturated bentonite buffer. Geological Society, London, Special Publications, 415(1), 189-201. 10.1144/SP415.12

Sellin, P., Harrington, J.F., 2006, Large-Scale Gas Injection Test (Lasgit) Current Status, American Nuclear Society High Level Waste Meeting, Las Vegas.

Swift, B.T., Hoch, A.R., Rodwell, W.R., 2001, Modelling gas migration in compacted bentonite: GAMBIT Club Phase 2, Final report (No. POSIVA-01-02), Posiva Oy.

Tamayo-Mas, E., Harrington, J.F., Shao, H., Dagher, E., Lee, J., Kim, K., Rutqvist, J., Lai, S., Chittenden, N., Wang, Y., Damians, I., Olivella, S., 2018, Numerical Modelling of Gas Flow in a Compact Clay Barrier for DECOVALEX-2019, Paper presented at the 2nd International Discrete Fracture Network Engineering Conference, 20-21, June, Seattle, Washington, USA.

Tamayo-Mas, E., Harrington, J.F., 2020, DECOVALEX-2019 Project: Task A Final Report. 10.2172/1762801

Tamayo-Mas, E., Harrington, J.F., Brüning, T., Shao, H., Dagher, E.E., Lee, J., Rutqvist, J., Kolditz, O., Lai, S.H., Chittenden, N., Wang, Y., Damians, I.P., Olivella, S., 2021, Modelling advective gas flow in compact bentonite: Lessons learnt from different numerical approaches, International Journal of Rock Mechanics and Mining Sciences, Vol. 139, pp. 104580. 10.1016/j.ijrmms.2020.104580

Tanai, K., Kanno, T., Gallé, C., 1996, Experimental study of gas permeabilities and breakthrough pressures in clays, MRS Symposia Proceedings, 465, 1003-1010. 10.1557/PROC-465-995

Tang, C.A., Tham, L.G., Lee, P.K.K., Yang, T.H., Li, L.C., 2002, Coupled analysis of flow, stress and damage (FSD) in rock failure, International Journal of Rock Mechanics and Mining Sciences, Vol. 39(4), pp. 477-489. 10.1016/S1365-1609(02)00023-0

The Grimsel Test Site in Switzerland, accessed October 1, 2021. available from [grimsel.com/gts-projects/]

Van Genuchten, M.T., 1980, A closed‐form equation for predicting the hydraulic conductivity of unsaturated soils, Soil science society of America journal, Vol. 44(5), pp. 892-898. 10.2136/sssaj1980.03615995004400050002x

Volckaert, G., Ortiz, L., De Cannière, P., Put, M., Horseman, S.T., Harrington, J.F., Fioravante, V., Impey, M., 1995, MEGAS - Modelling and Experiments on Gas Migration in Repository Host Rocks: Final Report Phase 1, European Commission Report EUR 16235 EN.

Vomvoris, S., Lanyon, B., Marschall, P., Ando., K., Adachi, T., Fujiwara, A., Yamamoto, S., 2003, Sand/bentonite barriers and gas migration: the GMT large-scale in-situ test in the Grimsel Test Site, Materials Research Society Proceedings on Scientific Basis for Nuclear Waste Management XXVI, Vol. 757, Materials Research Society, Warrendale, Pennsylvania. 10.1557/PROC-757-II3.27

Xu, W. J., Shao, H., Hesser, J., Wang, W., Schuster, K., Kolditz, O., 2013, Coupled multiphase flow and elasto-plastic modelling of in-situ gas injection experiments in saturated claystone (Mont Terri Rock Laboratory), Engineering Geology, Vol. 157, pp. pp. 55-68. 10.1016/j.enggeo.2013.02.005

Ye, W. M., Xu, L., Chen, B., Chen, Y.G., Ye, B., Cui, Y.J., 2014, An approach based on two-phase flow phenomenon for modeling gas migration in saturated compacted bentonite, Engineering geology, Vol. 169, pp. 124-132. 10.1016/j.enggeo.2013.12.001

Tunnel and Underground Space ISSN:1225-1275(Print) 2287-1748(Online) 터널과 지하공간

Preview

Introduction to Researches on the Characteristics of Gas Migration Behavior in Bentonite Buffer

ABSTRACT

MAIN

Fig. 1

Schematic view of experimental apparatus for gas migration utilizing MX-80 bentonite sample (Pusch and Forsberg, 1983)

Fig. 2

Schematic view of experimental apparatus for gas migration utilizing Kunigel V1 bentonite sample (Tanai et al., 1996)

Fig. 3

(a-b) Schematic view of gas migration apparatus used for 1- and 3-dimensional tests, (c) photograph of experimental setup, and (d) schematic view of the location of injection and radial filters (Harrington, 2016, Harrington et al., 2017)

Fig. 4

Fig. 5

Fig. 6

Concept of the GMT experiment at the Grimsel underground laboratory (Olivella and Alonso, 2008)

Fig. 7

Variations in liquid and gas pressure measured during the GMT experiment (from grimsel.com)

Fig. 8

Schematic view of the test site and test devices of Lasgit experiment (Sellin and Harrington, 2006, Cuss et al., 2011)

Table 1.

Schedule of Lasgit experiment including three preliminary gas injection tests (Cuss et al., 2014b)

Fig. 9

Variation in STP flow rate and gas pressure measured at FL903 during Lasgit test. First gas injection: (a) the first and (b) the second stage of gas injection. Second gas injection: (c) the first and (d) the second stage of gas injection (Cuss et al., 2011)

Table 2.

Comparison of pore pressure distribution prediction of numerical models suggested in DECOVALEX-2019

(1)

Table 3.

Models for swelling in barrier material

(6)

(7)

(8)

(9)

Fig. 10

TOUGH-RBSN concept of dilatant flow path creation as a result of reactivation of weak interfaces between porous aggregates: (a) before reactivation and (b) after reactivation of interfaces and creation of discrete fracture or flow path (Kim et al., 2021).

Fig. 11

Fracturing and propagation of dilatant flow paths: (a) continuum damage model(Lee et al., 2020e), (b) discrete rigid-body-spring network model (Kim et al., 2021)

Table 4.

Models for intrinsic permeability for gas migration in barrier materials (modified Table 2 in Guo and Fall, 2021)

Table 5.

Models for relative permeability for gas migration in barrier materials

Table 6.

Model selection chart for gas migration in clay material

Acknowledgements

References