1. 서 론

고준위방사성폐기물 심층처분장의 다중방벽시스템 중 천연방벽은 심층처분장을 둘러싼 암반으로 방사성핵종의 누출과 열 및 방사성 영향을 생태계로부터 차단하는 역할을 수행한다. 천연방벽은 고준위방사성폐기물이 안정화 될 때까지 성능을 유지해야 하기에, 장기간에 걸쳐서 충분한 열(thermal), 수리(hydraulic), 역학(mechanical), 화학적(chemical) 안정성을 보유해야 한다. 이러한 조건에 부합하는 심층처분시스템 대상 부지로는 주로 결정질암(crystalline rock), 점토질암(argillaceous formations), 암염(salt formations)이 고려되고 있으며(Kim and Kwon, 2017), 그중에서도 결정질 암반은 암석 자체의 높은 강도와 낮은 투수계수, 낮은 용해 특성에 따른 지구화학적 안정성을 보유하여 스웨덴, 핀란드를 비롯한 여러 국가에서 고준위방사성폐기물 심층처분 대상 암반으로 고려되고 있다(Table 1). 하지만 결정질암은 무결암의 낮은 투수계수에도 불구하고 취성(brittleness)이 높아 암반 내에 불연속면(discontinuity)이 생성(creation) 및 전파(propagation)될 수 있고, 불연속면의 수리학적 특성에 따라 유체의 잠재적 유동 경로가 형성될 수 있다. 이 경우 투수계수가 낮은 모암보다는 불연속면에 의해 암반 전체의 수리학적 특성이 결정되고, 결과적으로 결정질암 내 처분시스템의 수리학적 특성화 및 모델링에서도 불연속면에서의 복합적인 거동이 주요하게 다루어진다.

처분시스템의 수리학적 거동은 수리학적 특성뿐만 아니라 열, 역학, 화학적 특성에 상호적으로 영향을 받는 복합거동의 형태로 나타난다. 이러한 열-수리-역학-화학적 (THMC) 복합거동은 처분시스템 내 천연방벽, 그중에서도 암반 내 불연속면에서 주요하게 나타나기에 전체 처분시스템의 성능평가를 위한 모델링에서도 불연속면을 포함한 암반의 THMC 복합거동을 모사할 수 있는 해석기법이 요구된다. 기존에는 암반 및 구조물에서의 복잡한 복합거동을 모사하기 위해서 모델링 및 해석이 간편하고 새로운 영향요인의 도입이 용이한 연속체(continuum) 모델을 주로 활용하였다. 하지만 결정질암 기반 처분시스템의 모델링에서는 불연속면의 거동 모사가 필요하고, 연속체 기반 해석기법은 불연속면의 자세한 거동 모사가 어렵고 모사 시 해석 성능이 저하되는 등의 어려움이 있다. 이에 반해 불연속체(discontinuum)를 기반으로 한 해석기법은 모델 자체 특성에 의해 불연속면의 반영 및 거동 모사가 용이하여 불연속면을 포함하는 균열암반 복합거동 모델링 등에서 빈번하게 활용되고 있다. 본 기술보고에서는 불연속면을 포함한 매질의 복합거동 중 수리-역학적 복합거동을 불연속체 기반 해석기법으로 모사하는 방법과 모델링 사례에 대해 소개하고, 향후 고준위방사성폐기물 처분시스템 모델링에서 불연속체 기반 모델링의 적용 가능성에 대해 검토하고자 한다.

2. 균열암반 내 수리-역학 복합거동 특성

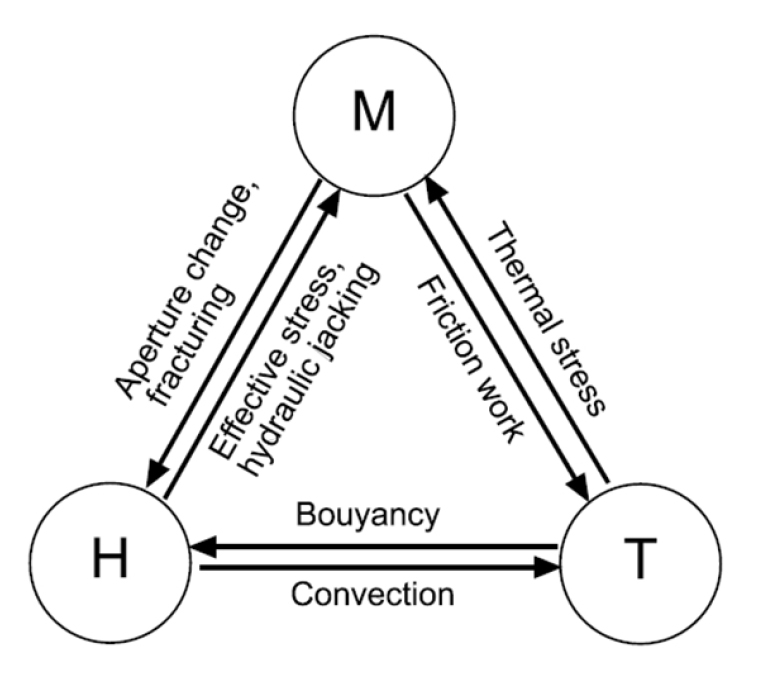
현장 조건에서 암반의 역학적 거동을 분석하기 위해서는 암반에 가해지는 모든 상호작용(interactions) 및 복합거동(coupled processes)을 충분히 이해하고 반영하여야 한다(Yow and Hunt, 2002). 그중에서도 암반 내에서 진행되는 열적, 수리학적, 화학적 거동은 암반의 역학적 물성 및 특성에 장단기적으로 유의미한 영향을 미칠 수 있고, 각각 열, 수리, 화학적 특성 간에도 상호 영향을 주고받기 때문에 암반의 역학적 거동 분석을 위해서는 열-수리-역학-화학적 복합거동에 대한 검토가 필요하다(Fig. 1).

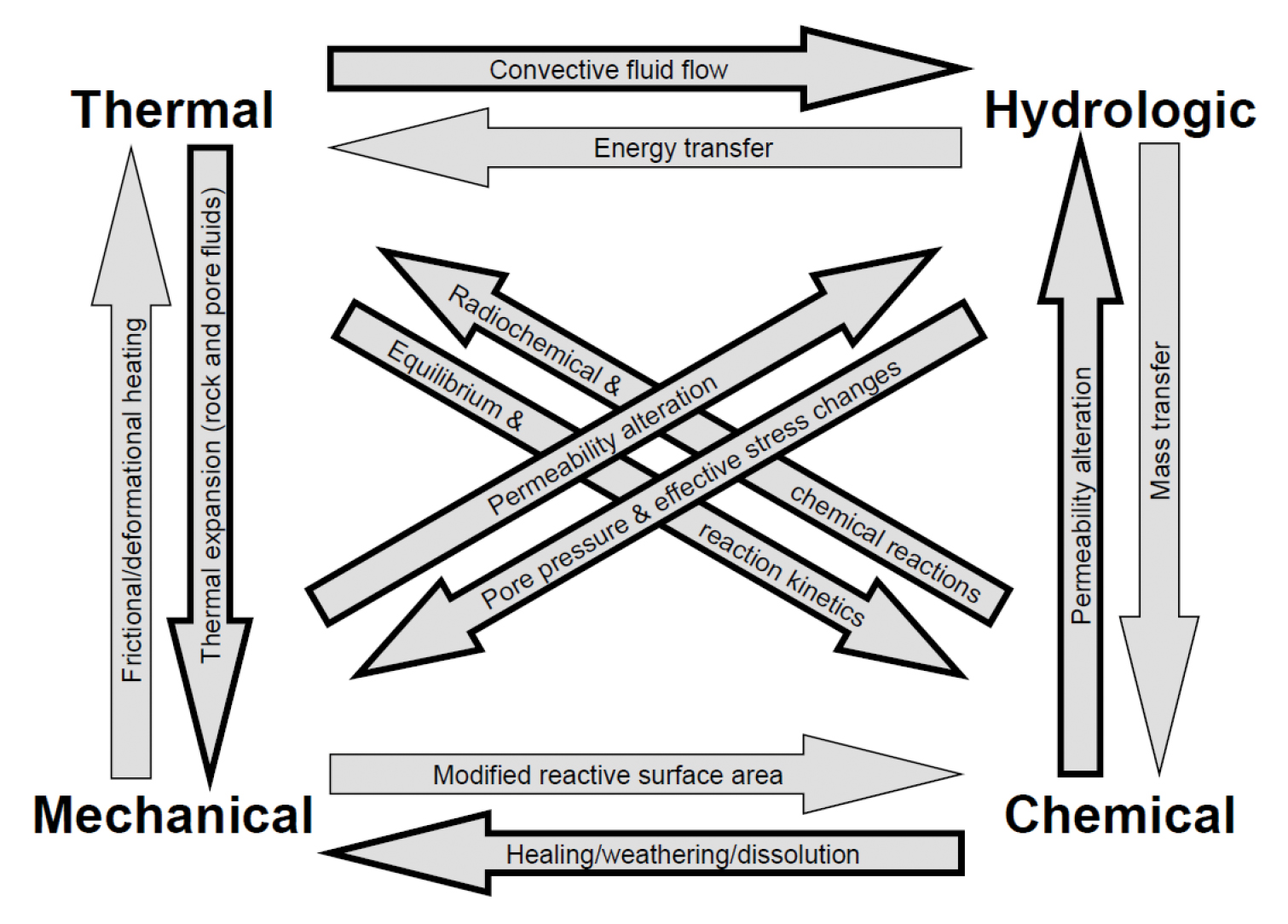
Fig. 1

Effects of coupled Thermal-Hydro-Mechanical-Chemical processes in rock mass (Yow and Hunt, 2002)

그중에서도 암반 내 수리-역학 복합거동은 심층처분시스템, 석유가스생산, 지열에너지, 이산화탄소지중저장 등 다양한 분야에서 필요로 하고, 수리학적 특성과 역학적 특성이 서로 민감하고 복잡하게 영향을 끼치기 때문에 현재까지도 많은 연구가 진행되고 있다. 수리-역학 복합거동의 기본 양상은, 역학적 시스템 내 응력 및 변위가 암반 투수계수(permeability) 및 공극률(porosity)의 변화를 일으켜 수리학적 시스템에 교란을 주고, 수리학적 해석으로 도출되는 유체 압력이 암반의 응력 상태에 변화를 야기하여 역학적 시스템에 교란을 주는 방식으로 진행된다. 이 과정에서 투수성 암반의 경우 공극률의 변화가 중점적으로 다뤄지며, 식 (1)과 같이 역학적 교란으로 인한 공극률의 변화를 구할 수 있다(Jaeger et al., 2007).

여기서 dØ는 공극률의 변화량, Ø₀는 초기 공극률, C_bc는 봉압에 의한 용적(bulk)압축률, C_m는 전체 용적압축률, P_c는 봉압, P_p는 공극압을 의미한다.

공극률에 미치는 역학적 영향을 더 간단하고 직관적으로 적용하기 위하여 Rutqvist and Tsang(2002)은 공극률과 평균 유효응력(mean effective stress) 간의 경험식을 식 (2)와 같이 제시하였다.

여기서 Ø_r는 높은 응력 하에서의 잔류(residual) 공극률, σ'M은 평균 유효 응력, a는 실험을 통해 얻어지는 상수이다.

다공성 매질에서의 유체유동특성은 부피균형(volume balance)식을 바탕으로 결정된다(식 3). 부피균형식에서의 비저류계수(specific storage, S_s)는 식 (4)와 같이 공극률에 의해 결정되기 때문에 마찬가지로 유체유동특성 또한 역학적 교란에 의해 영향을 받는다(Watanabe et al., 2010).

여기서 p는 유체 압력, q_f는 유량, u는 변위벡터, C _f는 유체의 압축률이며, ∇∙∂u∂t는 응력 변화로 인한 공극 부피 변화를 나타낸다. 유체 유량이 다르시의 법칙(Darcy’s law)에 의해 구해진다고 가정하면, 유량은 식 (5)와 같이 표현된다.

여기서 k는 고유 투수계수(intrinsic permeability), μ는 유체 점성계수, ▽p는 유체 압력의 경사, ρ_f는 유체 밀도, g는 중력가속도, ▽z는 기준 심도의 경사를 의미한다. 투수계수 역시 역학적 영향에 따라 변화하며, Rutqvist and Tsang(2002)에 의해 공극률과의 경험식으로 식 (6)과 같이 제시되었다.

여기서 c는 실험을 통해 결정되는 상수이다.

역학적 시스템에 의해 변화한 수리학적 인자를 바탕으로 유량과 유체 압력이 결정되면, 계산된 유체 압력이 다시 역학적 시스템에 영향을 미친다(식 7)(Jaeger et al., 2007).

여기서 ε는 변형률 텐서, τ는 응력 텐서, G는 전단계수, ν는 포아송 비, α는 비오 계수(Biot coefficient), K는 체적탄성계수(bulk modulus)를 의미한다.

암반에 불연속면이 존재하는 경우, 암반 전체의 수리학적 거동이 불연속면의 연결도 및 투수계수에 따라서 결정된다. 따라서 불연속면을 포함하는 암반의 복합거동해석이 중요하다. Fig. 2는 불연속면에 초점을 맞춘 균열암반에서의 열-수리-역학 복합거동 양상을 보여주고 있다. 균열암반에서의 수리-역학 복합거동은 기존 투수성 암반의 복합거동과 더불어 균열의 간극(aperture) 변화 및 새로운 균열 생성에 의한 영향을 포함하고 있다.

Fig. 2

Joint rock mass couplings (Hökmark et al., 2010)

불연속면을 통해 유체가 흐르는 경우, 불연속면의 간극이 수리전도 특성을 결정한다. 불연속면의 간극을 통해 투수량계수를 계산하는 가장 간단한 모델은 삼승법칙 (Cubic law)을 활용하여 두 개의 매끄러운 면이 일정한 간격(h)을 갖고 평행하게 떨어져 있는 경우에 면 사이에 존재하는 공간의 투수량계수(T)를 계산하는 것이다(Zimmerman and Bodvarsson, 1996). 간격(h)은 불연속면에서 수리학적 간극으로 대체된다(식 8).

여기서 w는 균열의 폭을 의미한다.

불연속면의 간극은 유효 응력 및 불연속면의 역학적 특성에 따라 열리거나 닫힐 수 있다. 불연속면에 가해지는 응력은 방향에 따라 각각 수직 및 전단 변형으로 나타난다(식 9, 10). 수직 응력에 따른 불연속면의 수직 변위는 직접적으로 간극의 열림 및 닫힘으로 연결되어 수리학적 특성에 영향을 줄 수 있다.

여기서 Δσ_n 및 Δτ_s는 유효 수직 및 전단 응력 변화량, k_n 및 k_s는 불연속면 수직 및 전단 강성, Δune 및 Δuse는 수직 및 전단 변위의 탄성 요소이다.

불연속면에 일정 강도 이상의 전단응력이 가해지면 파괴가 발생하여 전단 미끄러짐(shear slip)이 발생한다. 불연속면의 전단 강도를 추정하는 가장 간단한 식은 쿨롱(Coulomb) 조건식(식 11)으로 불연속면에 가해지는 수직 응력에 따라 선형적으로 전단 강도(τmax)가 증가한다. 전단 응력이 전단 강도에 다다른 이후에는 잔류 전단 응력(residual shear stress)를 유지하며 비가역적인 전단 변위가 발생한다.

여기서, C는 불연속면의 점착강도, Ø_f는 불연속면의 마찰각, Δu_s는 전단 변위를 의미한다.

전단 미끄러짐이 발생하는 동안, 불연속면의 거칠기 특성에 따라 간극의 팽창이 발생할 수 있다. 미끄러짐으로 인한 간극의 팽창은 불연속면 투수계수의 비가역적인 증진을 야기할 수 있다. 전단 팽창 특성은 불연속면의 거칠기, 방향성, 강도, 충진물에 관련되어 복잡한 형태로 나타나지만(Olsson and Barton, 2001), 일반적으로는 불연속면의 거칠기 및 강도를 포함한 역학적 물성인 팽창각(dilation angle, Ø_d)을 활용하여 식 (12)와 같이 표현되는 팽창 특성이 활용된다(Barton and Choubey, 1977).

여기서 Δuns는 수직 변위의 전단 요소를 뜻한다.

이렇게 수직 변형과 전단 팽창으로 인해 변화하는 불연속면의 간극은 전체 암반의 수리학적 특성에 유의미한 변화를 줄 수 있다. 따라서 결정질 암반을 대상으로 하는 복합거동 해석에서는 불연속면의 거동을 자세하고 정확하게 표현하는 방법에 초점을 맞추어 진행된다.

3. 불연속체 기반 수리-역학 복합거동 해석기법 현황

3.1 UDEC/3DEC

UDEC 및 3DEC은 미국 Itasca Consulting Group Inc.에서 개발한 2차원 및 3차원 블록 기반 개별요소법(distinct element method) 프로그램으로(Itasca, 2018, 2019), 모델링 대상을 개별 블록(discrete block)들의 집합체로 구현하여 각각 블록의 움직임으로부터 전체 모델의 거동을 해석한다. 블록 간의 접촉면(contact)에서 블록의 상대적인 움직임에 따른 상호작용이 계산되고, 접촉면에 설정된 구성방정식에 의거하여 수직 및 전단 거동이 결정된다. 접촉면 자체의 움직임은 다시 탄성에 의해 맞닿은 블록에 새로운 외력을 작용하여 블록 자체의 움직임 및 변형을 야기한다(Jing, 2003). 이렇게 모델을 구성하는 블록과 접촉면 사이의 역학적 상호작용이 반복되면서 전체 모델의 역학적 거동이 결정된다. 블록 간의 접촉면에서 복잡하고 구체적인 거동을 반영할 수 있는 특성상 UDEC/3DEC은 불연속면을 포함한 암반의 역학적 거동을 모사하는 데 주로 활용된다. 주로 수직 및 전단 변형과 전단 미끄러짐을 통해 불연속면의 거동이 해석되며, 사용자가 지정한 모델 및 불연속면 물성에 따라 전단 변위에 의한 불연속면 간극의 팽창(dilation) 또한 구현할 수 있다.

UDEC/3DEC에 포함된 수리학적 해석 모듈에서는 모델 내에 존재하는 불연속면을 따라서 진행되는 유체 유동을 분석할 수 있다. 실제 결정질암과 같은 낮은 무결암 투수계수를 가진 암반에서 비교적 높은 투수계수를 갖는 균열망을 따라 흐르는 유체 유동 양상을 본 수리학적 해석 모듈을 통해 모사할 수 있다. 단일 불연속면의 투수계수는 불연속면의 간극으로부터 삼승법칙에 따라 식 (8)과 같이 계산된다.

여기서 UDEC/3DEC에서의 불연속면 간극은 불연속면에 작용하는 응력에 따라서 수직 변형 및 전단 팽창을 거쳐서 변화한다. 구축된 불연속체 모델에서 유체 유동이 불연속면의 간극으로부터 계산된 수리학적 특성에 따라서 결정되기 때문에, 역학적 해석이 진행됨에 따라 모델의 유체 유동 특성 또한 변화한다. 수리학적 특성의 변화를 실시간으로 반영하기 위해서 UDEC/3DEC에서는 수리-역학적 복합거동 옵션을 제공하여 일정 역학적 계산 주기마다 업데이트되는 불연속면의 간극을 수리학적 해석 알고리즘에 적용시킨다. 또한, 수리학적 해석 결과로 도출되는 불연속면에서의 유체 압력도 모델 내 역학적 해석 조건에 일정 해석 주기마다 업데이트하여 수리학적 거동이 미치는 역학적 교란을 반영할 수 있다. 이렇게 UDEC/3DEC에서는 불연속체 내 불연속면에서의 유체 유동에 집중하여 수리-역학적 복합거동을 구현하며, 실제 암반 내 균열 및 절리를 따라 흐르는 유체의 거동을 모사하는 데에 특화되어 활용된다.

UDEC/3DEC 기반 수리-역학 복합거동 해석은 앞서 설명한 프로그램 내부 수리역학적 복합거동 해석 모듈을 활용하여 불연속면 내 유체 흐름을 대상으로 이루어진다. Zhang et al.(1996)은 UDEC을 활용하여 균일한 간격을 갖는 균열 패턴을 생성하고, 하중 조건에서 균열의 방향에 따라 균열암반의 투수계수가 바뀌는 양상을 확인하였다. 암반에 내포된 균열의 투수계수가 전체 암반의 수리학적 인자를 결정하였고, 균열에 작용한 유효 수직응력이 간극을 여닫으면서 수리학적 특성에 영향을 미치는 방식으로 균열암반에서의 수리-역학 복합거동을 나타내었다. Min et al.(2004)은 UDEC을 기반으로 암반균열망(Discrete Fracture Network, DFN)을 포함한 균열암반 모델을 구축하고, 균열암반에 작용하는 초기응력에 따른 투수계수 변화를 분석하였다. 균열 투수계수 변화는 균열 자체의 수직 변형 및 전단 팽창으로 인한 간극 변화로부터 구현되었고, 모델에 적용된 경계응력을 각각 균등하게 혹은 방향에 따라 차등적으로 증가시켰을 때 균열에 나타나는 간극 및 투수계수 변화를 확인하였다(Fig. 3). 일반적으로 경계응력의 증가는 균열의 수직 닫힘으로 인한 투수계수의 감소를 야기한다. 하지만 경계응력이 한 쪽 방향으로만 차등하게 증가하는 경우 일부 균열에서 전단응력이 집중되어 전단 미끄러짐으로 인한 간극 팽창이 발생하여 투수계수가 오히려 증가하는 양상이 확인되었다. Min and Stephansson(2011)은 앞서 검토한 UDEC 내 수직 및 전단 거동에 의한 수리역학적 복합거동 모듈을 바탕으로 스웨덴의 사용후핵연료 처분시설 부지로 검토 중인 포쉬마크(Forsmark)지역에서의 현지 응력에 의한 투수계수 변화를 확인하고자 하였다. 포쉬마크 지역의 암반균열망 데이터를 바탕으로 2차원 균열암반 모델을 구축하고, 응력 변화에 따른 균열의 간극 및 투수계수 변화를 바탕으로 유체의 유동 경로를 예측하였다.

Fig. 3

Fluid pathways under various stress applications with the direction of hydraulic pressure gradient (a) from right to left and (b) from top to bottom (Min et al., 2004)

3DEC 역시 3차원 블록 사이의 불연속면을 통해 흐르는 유체 유동을 바탕으로 불연속체의 수리-역학적 복합거동을 해석한다. 3DEC은 3차원 해석기법인 만큼 불연속면을 포함한 부지 및 구조물을 모델링하는 응용 분야에 주로 활용된다. Mas Ivars.(2006)는 단일 균열을 포함한 암반에 터널을 굴착했을 때 터널 내부로 유입되는 유량을 3DEC 내 수리-역학적 복합거동 해석기법을 활용하여 분석한 바 있다. 고려된 단일 균열은 터널을 포함한 모델 전체를 지나도록 형성되었고, 균열의 물성 및 역학적 모델을 바꿔가며 터널 내 유입 유량의 변화를 확인하였다(Fig. 4). 균열의 역학적 모델의 경우 연속 항복(Continuously yielding) 모델(Itasca, 2019)을 활용하여 비선형적인 수직 및 전단 변형이 반영되었다. 결과적으로 균열의 수직 변형 및 전단 팽창이 복합적으로 수리학적 특성에 영향을 미칠 수 있고, 균열의 응력 상태와 수직 및 전단 강성, 팽창각, 마찰각을 고려한 복합적인 거동 분석이 필요함을 확인하였다.

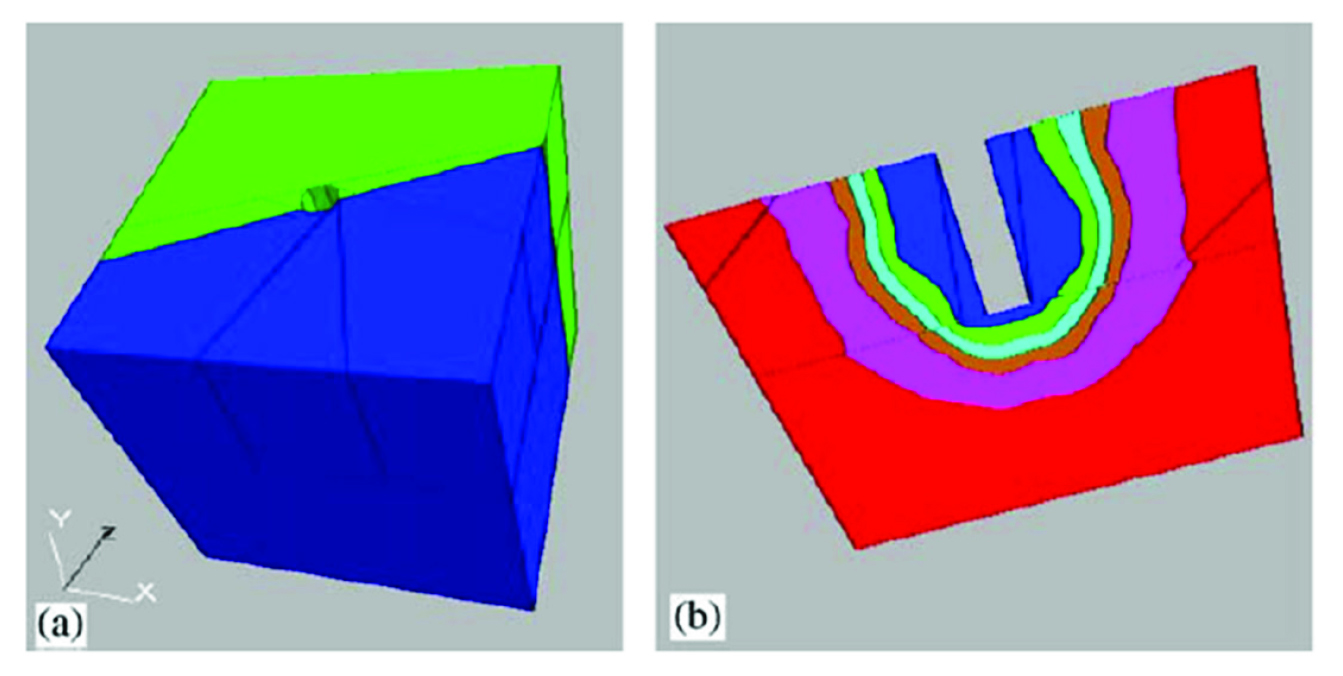
Fig. 4

(a) Geometry of tunnel model and (b) aperture distribution on the fracture surface (Mas Ivars, 2006)

Yin et al.(2020)는 유체 주입 및 배수(backflow)에 따른 단층 재활성(fault reactivation) 및 그에 따른 유발지진을 3DEC을 활용하여 모사하였다. 단층 및 수압파쇄 면을 모델 내 불연속면으로 구현하고, 비선형 쿨롱 미끄러짐 모델(Zhang et al., 2020)을 바탕으로 불연속면의 수직 변형 및 전단 미끄러짐을 모사하였다. 3DEC 내에서 불연속면의 간극 변화를 바탕으로 진행되는 수리-역학적 복합거동 해석기법을 활용하여 유체 주입 및 배수가 진행됨에 따라 나타나는 유체 압력 및 균열 투수계수 변화를 반영하여 단층의 역학적인 움직임을 정량화하였으며, 단층에 나타난 응력 변화 및 변위를 바탕으로 발생할 수 있는 유발지진을 추정하였다(Fig. 5).

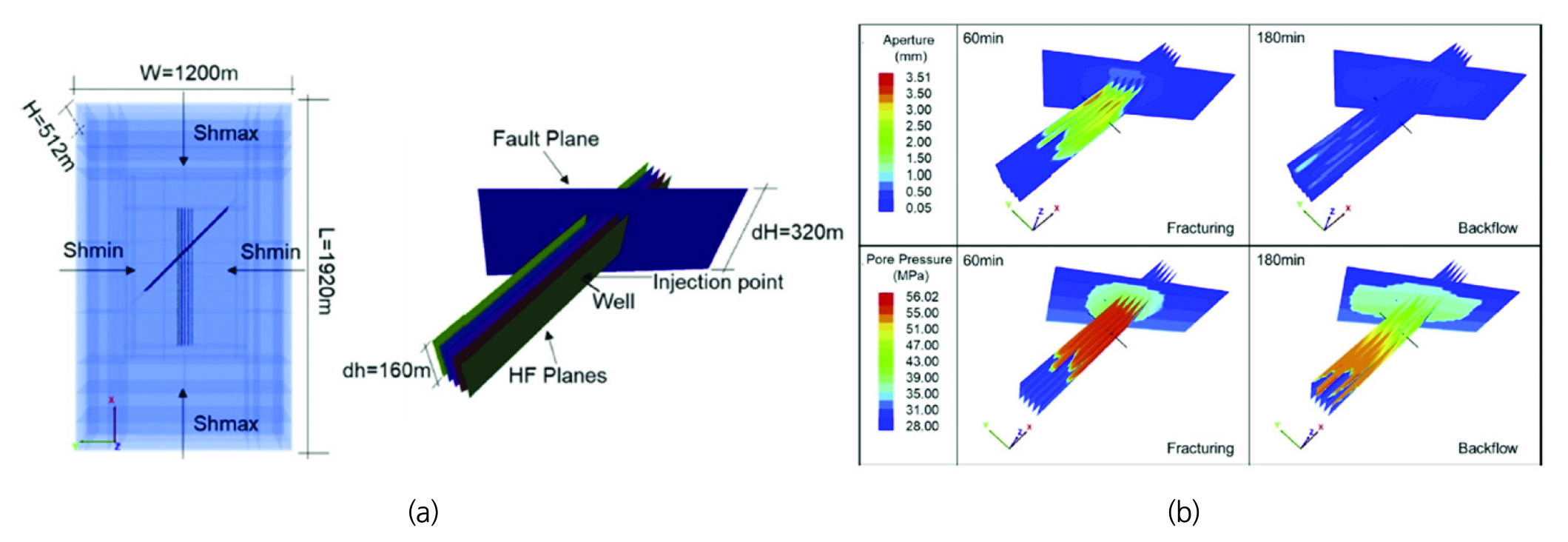
Fig. 5

(a) Geometry of models and (b) aperture and pore pressure distributions during injection and backflow (Yin et al., 2020)

Park et al.(2021)은 균열을 내포한 암석에서의 수리역학 복합거동을 모사하기 위해 3DEC을 활용한 입자기반 개별요소모델(grain-based distinct element model)을 활용하였다. 입자기반 개별요소기법은 암석을 광물과 같은 미세입자들의 결합으로 표현하고자 다면체 입자들의 결합체로 지정된 모델을 모사한다. 이 경우 균열의 생성, 전파 등의 자세한 균열 거동을 표현할 수 있는 장점이 있지만, 암석 및 균열의 역학적 물성을 정확하게 재현하기 어려운 한계점이 있다. 이러한 입자기반 개별요소기법을 바탕으로 유한한 단일 균열을 내포하는 암석 모델을 구축하고, 균열 내에 유체를 주입하였을 때 발생하는 암석 및 균열의 변위를 검토하였다. 입자기반 개별요소기법으로 구축한 균열암반 모델 해석 결과를 균열 열림과 관련된 정해(Parker, 1981)와 비교한 결과 해당 정해를 성공적으로 모사할 수 있음을 확인하였다.

3.2 PFC

PFC(Particle Flow Code)는 미국 Itasca Consulting Group Inc.에서 개발한 2차원 및 3차원 입자결합(bonded-particle) 개별요소법 프로그램으로(Itasca, 2021), 모델링 대상을 다수의 원형(2D) 혹은 구형(3D) 입자들의 집합체로 구현한다. 입자는 변형되거나 파괴되지 않는 강체(rigid body)로 구현되며, 대신 입자 사이 접촉면(contact)에 존재하는 결합(bond)이 입력된 강성 및 강도를 바탕으로 입자 간의 상대적인 힘과 입자의 움직임을 결정한다(Potyondy and Cundall, 2004). 이렇게 개별적으로 계산된 입자의 거동을 합쳐서 전체 모델의 역학적 거동을 표현하는 것이 입자결합 모델의 기본 알고리즘이다. 입자결합 모델은 입자 간 결합에 각각 다른 미세물성(micro-parameters) 및 미세메카니즘(micro-mechanism)을 설정할 수 있으며, 특정 구역에 전체와 다른 미세물성을 반영함으로써 균열, 절리, 단층, 연약면 등의 불연속면을 구현할 수 있다(Potyondy and Cundall, 2004, Park and Min, 2015, Lei et al., 2017). 특히 입력된 결합의 강도를 바탕으로 파괴를 모사하여 불연속면의 생성 및 전파 또한 구현할 수 있기에, 불연속체의 정성적 거동을 보다 사실적으로 표현할 수 있다는 장점이 있다.

PFC를 활용한 2차원 수리-역학적 복합거동 해석은 Cundall(2000)에 의해 제시되고 Hazzard et al.(2002)에 의해 소개된 바 있다. 입자결합 모델 내에서는 입자로 둘러싸인 공간을 공극(pore space)으로, 입자 간 접촉면을 유동 경로(flow channel)로 가정한다(Fig. 6). 유동 경로를 통해 연결된 두 개의 공극 내 유체 부피 및 압력에 따라 유동 경로에서의 유체 유동이 결정된다. 유동 경로를 따른 유량은 접촉면에 저장된 간극 데이터를 바탕으로 삼승법칙을 활용하여 계산된다. 접촉면에서의 간극은 시뮬레이션 과정에서 접촉면에 작용하는 수직응력을 바탕으로 식 (13)와 같이 계산되었다(Yoon et al., 2014).

여기서 e는 접촉면의 수리학적 간극, e _inf는 높은 수직응력 상태의 간극, e₀는 수직응력이 없을 때의 간극, σ_n는 접촉면에 가해진 수직응력을 의미한다.

수직응력에 의해 바뀌는 간극은 수리학적 교란을 야기하고, 수리학적 거동으로 변화하는 공극 내 유체 압력은 주변 입자에 가해져 역학적 교란을 야기한다. 이와 같은 역학적 해석과 수리학적 해석 간 상호작용을 통해 입자결합 해석기법을 활용하여 불연속체에서의 수리-역학적 복합거동을 모사할 수 있다.

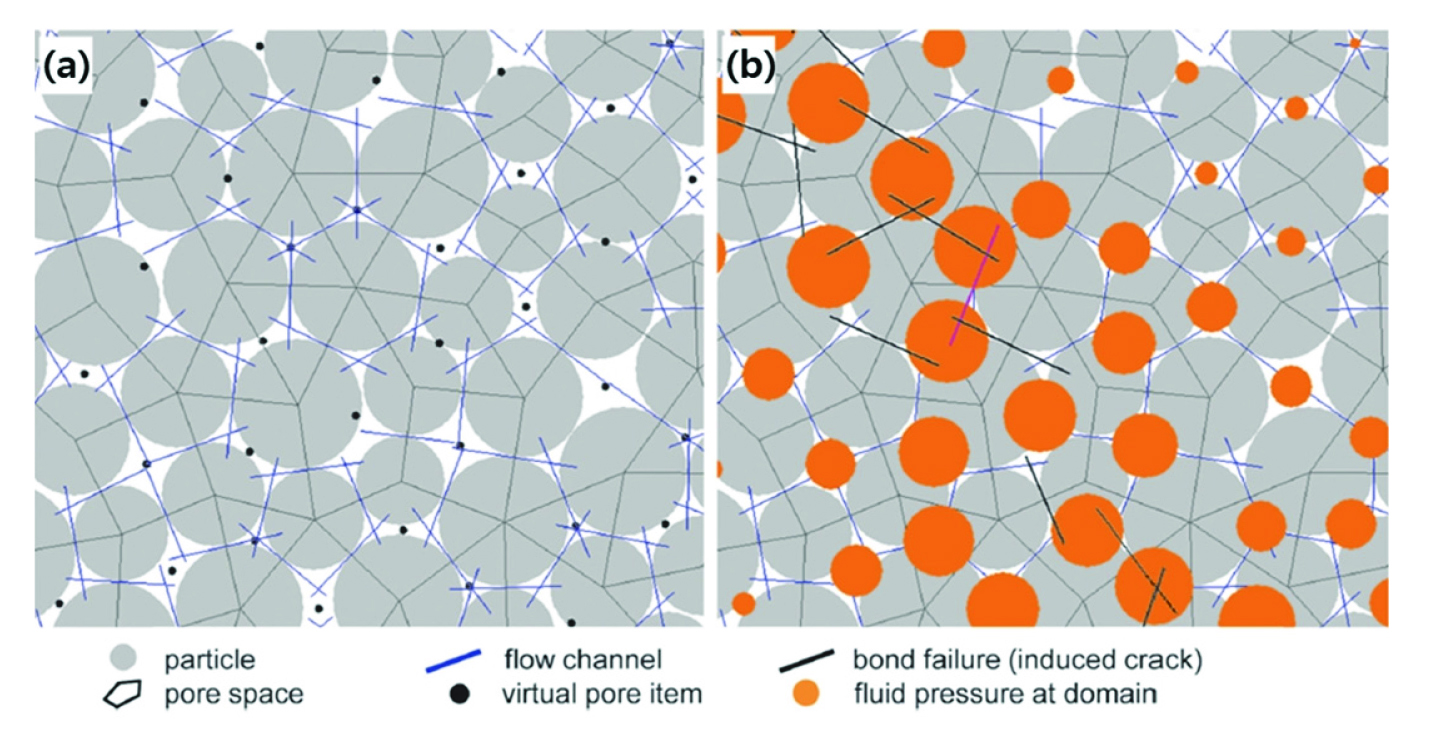
Fig. 6

(a) Pore space network and flow channel within the bonded particle model and (b) distribution of fluid pressure and induced bond failures (Yoon et al., 2015)

Yoon and Zhou(2020)는 PFC로 구현된 3차원 입자결합 모델에서의 수리-역학적 복합거동 역시 3차원 공극과 공극들 사이를 연결하는 유동 통로(flow pipes) 개념을 활용하여 구현하였다. 간극을 대신한 2차원 유동 경로와 달리 3차원 모델 내 유동 통로는 원통 형태로 식 (14)와 같은 압력 구배에 따른 유량(q)을 발생시킨다.

여기서 r은 유동 통로의 반경, ΔP는 인접 공극 사이의 압력 구배, L은 유동 통로의 길이, μ는 유체의 점성계수를 의미한다.

PFC에서의 수리-역학적 해석 메카니즘은 공극에서의 거동과 불연속면에서의 거동을 모두 고려할 수 있기 때문에, 불연속면을 포함한 다공성 매질에서의 수리-역학적 해석에 응용될 수 있다. 대표적으로 저류층에 유체를 주입하여 불연속면을 생성하는 수압 파쇄(hydraulic fracturing) 및 이미 존재하는 불연속면에 전파, 변형, 미끄러짐을 발생시키는 수리 자극(hydraulic stimulation)의 모델링에 PFC 기반 수리-역학적 해석기법이 활용된 바 있다(Hazzard et al., 2002, Tomac and Gutierrez, 2017, Yoon et al., 2014, Yoon et al., 2017, Yoon and Zhou, 2020). Hazzard et al.(2002)는 2차원 입자결합모델 내 유동 경로 개념을 활용하여 수리-역학 복합거동 해석이 가능한 저류층 모델을 구축하였다. 프랑스 슐츠(Soultz) 지역 지열저류층의 물성을 활용하여 저류층 모델을 구성하는 입자 및 결합의 특성을 결정하였고, 실제 슐츠지역 GPK2 공에서 수행되었던 유체 주입 시험의 조건을 반영하여 수리-역학적 수치해석을 수행하였다. 유체를 주입함에 따라 균열이 전파 및 변형되는 양상이 입자결합모델을 통해 모사될 수 있었으며, 균열의 전파가 진행되면서 발생하는 지진의 규모를 정량화할 수 있었다.

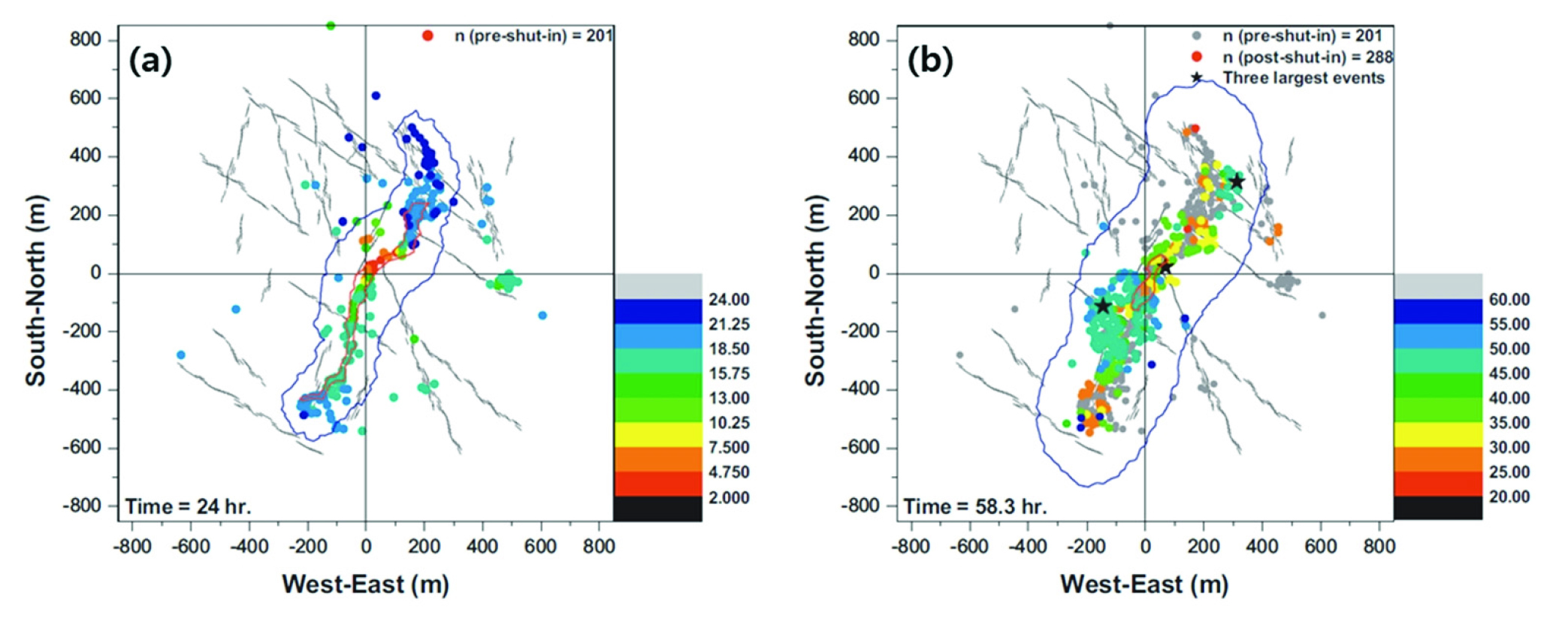
Fig. 7

Distribution of the induced seismic events during (a) pre-shut-in and (b) post-shut-in with monotonic injection in two-dimensional bonded-particle model (Yoon et al., 2014)

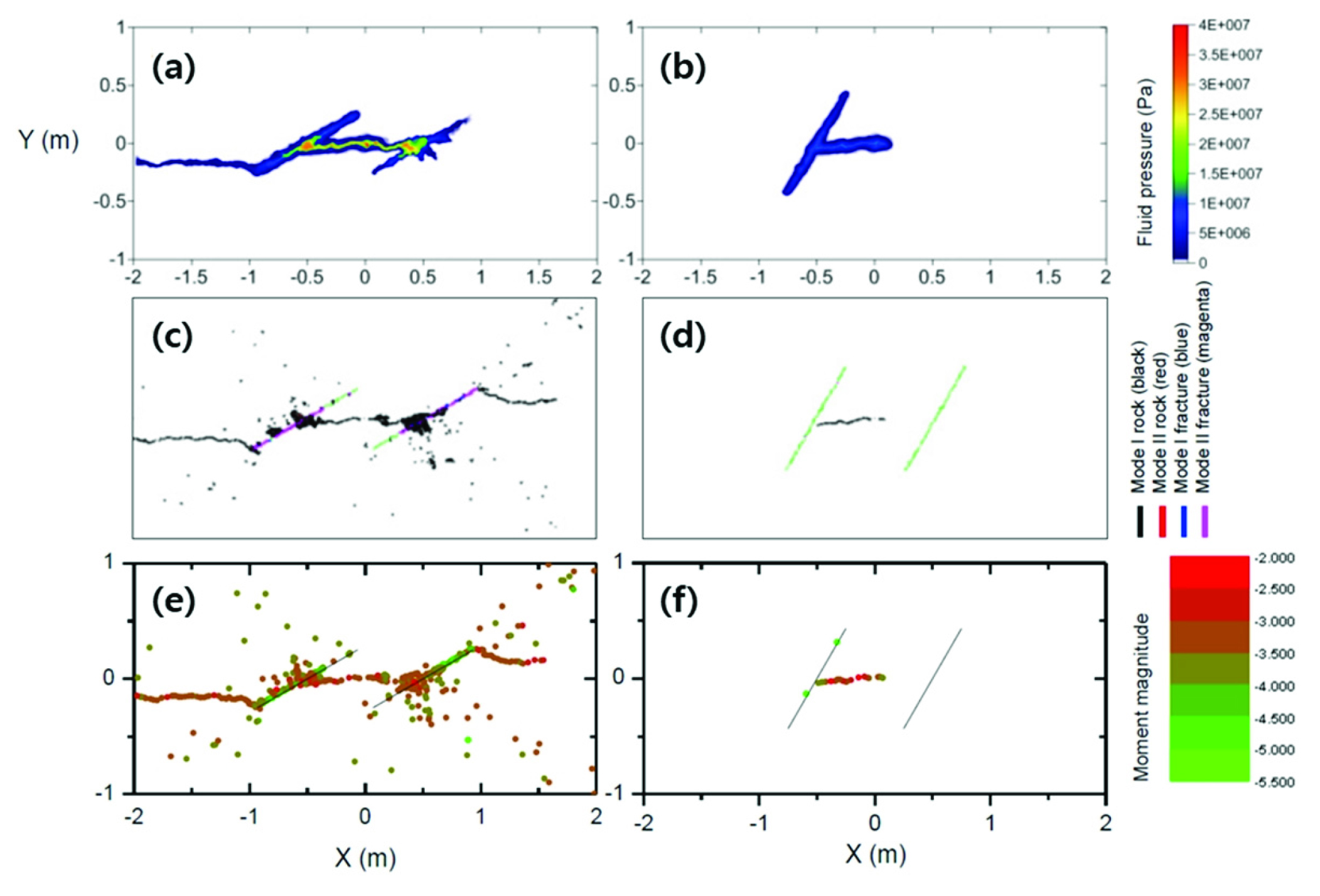
Fig. 8

Fluid pressure distribution (a & b), cracks in PFC2D (c & d) and seismic events at the end of fluid injection (e & f) with 30° inclined two natural fractures and 60° inclined two natural fractures (Yoon et al., 2017)

Yoon et al.(2014)은 2차원 입자결합 해석기법을 기반으로 암반균열망이 존재하는 저류층 모델을 구축하였으며, 저류층에 유체를 주입하는 방식에 따라 균열이 전파되는 양상과 유체 유동의 진행을 확인하였다. 균열이 변형 및 전파됨에 따라 발생하는 유발 지진 또한 시간 및 규모에 따라 분석하였다(Fig. 7). Yoon et al.(2017)은 이후 2차원 입자결합 모델을 바탕으로 한 수압파쇄 시뮬레이션에서 유체 주입에 따른 자연 균열(natural fracture)의 전단 미끄러짐, 팽창, 변형을 모두 모사할 수 있으며, 균열 전파 메커니즘에서도 Mode 1 기반의 날개 모양 균열(wing crack) 형태의 전파 과정을 표현할 수 있음을 보였다(Fig. 8). Tomac and Gutierrez (2017)는 2차원 입자결합 모델로 시추공을 구현하고 나공에서의 수압파쇄 실험을 열-수리-역학적으로 모사하였다. 열 및 압력에 따른 미세균열(micro-fracture)의 생성을 입자간 결합의 파괴로 모사하고, 유체 주입에 따른 암반 내 열 및 수리학적 교란을 바탕으로 공벽에서의 균열 전파를 모사하였다.

Yoon and Zhou(2020)는 스위스 Mont Terri 지하연구시설에서 진행된 단층 내 유체 주입 실험을 3차원 입자결합 개별요소법 해석 프로그램을 활용하여 모사하였다. 현장에서 관측된 2 m 두께의 단층대를 손상대와 코어균열로 구현하여 단층대를 통한 유체 유동을 모사하고자 하였다. 3차원 입자결합 모델의 유동 통로 개념에 기반하여 유동 통로의 반경을 조절하여 암석과 단층대의 투수계수 차이를 반영하였고, 단층대에 집중적으로 나타나는 유체 압력을 수치해석 결과를 통해 확인할 수 있었다(Fig. 9).

Fig. 9

Fluid pressure distribution by time on the fault plane in three-dimensional bonded-particle model (Yoon and Zhou, 2020)

3.3 DDA

DDA(Discontinuous Deformation Analysis)는 Shi and Goodman(1985)에 의해 처음으로 소개된 수치해석 기법으로, 블록과 접촉면으로 구성된 개별요소 모델의 역학적 거동에 대한 내연적(implicit) 해석을 제공한다(Lisjak and Grasselli, 2014). 개별요소로 이루어진 전체 모델에 대한 지배방정식(governing equation)을 구축하며, 블록 자체의 변형뿐만 아니라 접촉면의 변형 및 미끄러짐 또한 고려할 수 있어 불연속면을 포함하는 암반을 모사하는 데에 특화되어있다. 초기에는 2차원 불연속체에 대한 해석만 제공되었으나, Shi(2001)에 의해 3차원 블록 시스템에 대한 DDA 해석기법 또한 개발되어 상용화되었다. DDA의 경우 외연적(explicit) 해석기법과 비교했을 때 (1)준정적(quasi-static) 해석과정에서 평형(equilibrium) 상태 도출이 용이하고, (2) 동적 해석에서의 단위시간(time step) 조절이 안정적이고, (3) 요소 내 해석과정에서 가우시안 구적법(Gaussian quadrature)이 필요하지 않고, (4) 유한요소법 코드와의 연동이 용이하다는 장점이 있다(Jing, 2003).

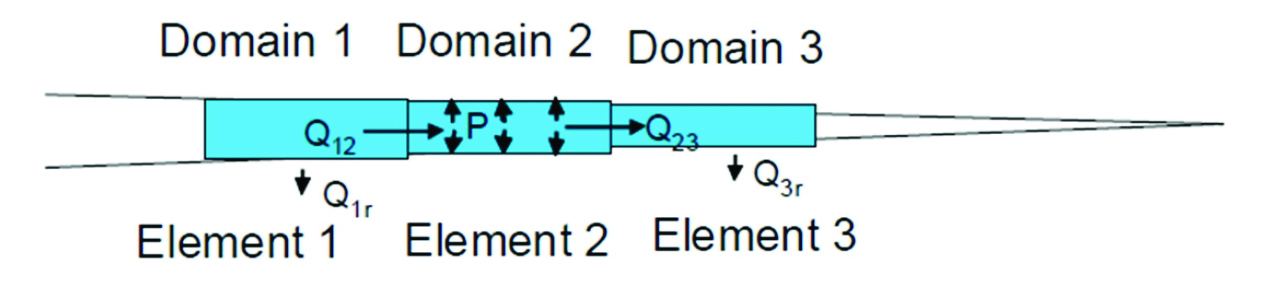
Fig. 14은 DDA 해석 코드에 모델 내 불연속면에서의 유체 유동 알고리즘을 추가하여 수리-역학 복합거동 해석 모듈을 구축하였다. 구축된 DDA 내 수리-역학 복합거동 해석 모듈은 앞서 블록 기반 개별요소법에서의 알고리즘과 흡사하게 불연속면의 역학적 거동에 따라 수리학적 특성이 변화하는 방식을 취하고 있다. 블록 자체는 불투수성으로 가정하였고, 균열을 따라서 층류(laminar flow) 및 단상(singe-phase)의 뉴토니안(Newtonian) 유체로 가정하였다. 역학적 해석이 진행되면서 불연속면의 간극은 수직 변형과 전단 팽창에 따라 변화하며, 삼승법칙을 바탕으로 균열의 수리학적 성능으로 변환된다. 역학적 해석을 통해 실시간으로 변화하는 간극은 수리학적 해석을 통해 새로운 유량과 유체 압력을 제시한다(Fig. 10). 이러한 역학적 해석과 수리학적 해석 간의 상호작용을 통해 불연속체 모델에 대한 수리-역학적 복합거동을 확인할 수 있다.

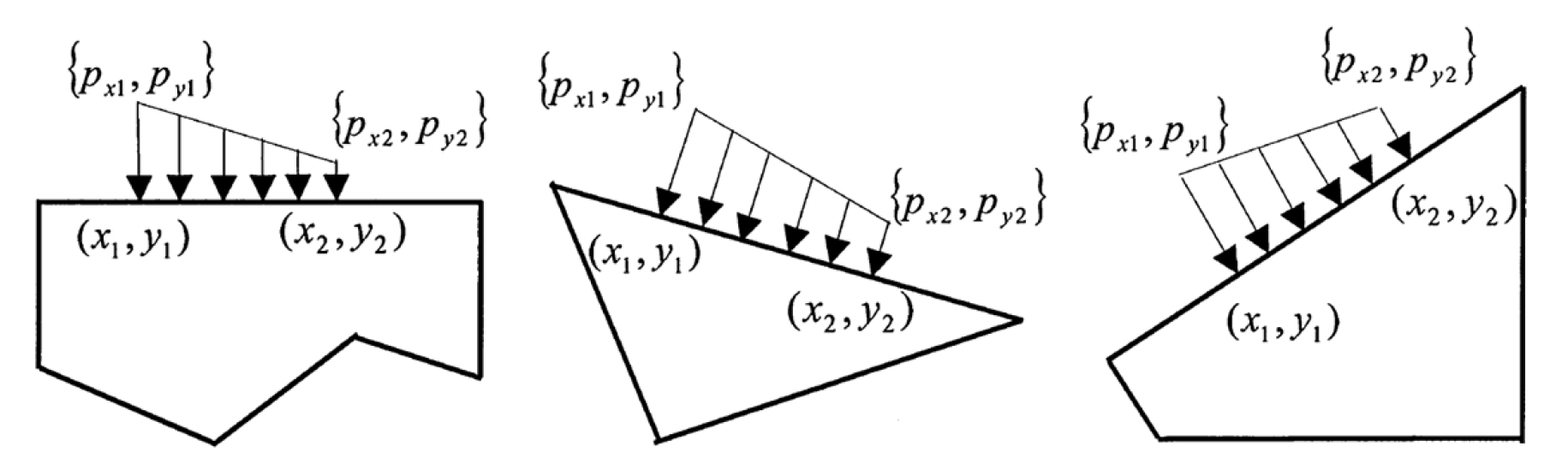
Fig. 10

Fluid pressure applied on (a) a rigid block, (b) triangular element and (c) a quadrilateral element in DDA (Jing et al., 2001)

불연속면 내 유체 유동을 바탕으로 수리-역학적 해석 알고리즘을 탑재한 DDA 해석기법은 수압파쇄와 같은 균열암반 대상 복합거동 응용 분야에 주로 활용되었다(Ben et al., 2013, Choo et al., 2016, Jiao et al., 2015, Morgan and Aral, 2015). Ben et al.(2013)은 해석 사이클마다 새로이 생성되는 불연속면을 포함하여 수리-역학적 해석을 수행하는 불연속체 전파 모델을 활용하여 2차원 HFDDA(Hydraulic Fracture modelling based on the Discontinuous Deformation Analysis) 해석기법을 구축하였다. 구축된 수압파쇄 DDA 해석기법은 불연속면의 생성 및 전파를 정성적으로 표현할 수 있었으며, 해석 사이클마다 업데이트 되는 불연속면 연결도 및 간극을 바탕으로 수리학적 거동을 분석하였다.

Jiao et al.(2015)은 DDA 해석기법을 바탕으로 수압파쇄를 모사하기 위하여 Jiao et al.(2012)이 구축한 DDARF(Discontinuous Deformation Analysis for Rock Failure)를 활용하여 수리-역학적 해석을 수행하였다. DDARF 기반 수리-역학적 해석기법은 해석과정에서 블록 경계에 가해지는 역학적 조건을 바탕으로 새로운 불연속면의 생성 여부를 판단하고, 생성되었을 경우 다시 수리-역학적 해석을 통해 블록의 안정성을 검토한다. 불연속면이 더 생성되지 않을 때까지 반복되며, 새로이 구축된 불연속체 모델을 바탕으로 수리-역학적 해석을 수행하여 결과를 도출한다. Fig. 11은 구축한 DDARF 해석기법을 활용하여 수압파쇄 실험을 모사한 수치해석 결과이다. 실제 원형 시추공과 20 mm 길이의 수평 방향 선재균열(precrack)을 포함한 암석 샘플의 공벽에 0.8 MPa의 유체 압력을 가하는 수압파쇄 실험을 진행하였고, DDARF 수치해석 결과와 비교한 결과, 수압파쇄로 인한 균열의 전파 과정을 성공적으로 모사할 수 있었다.

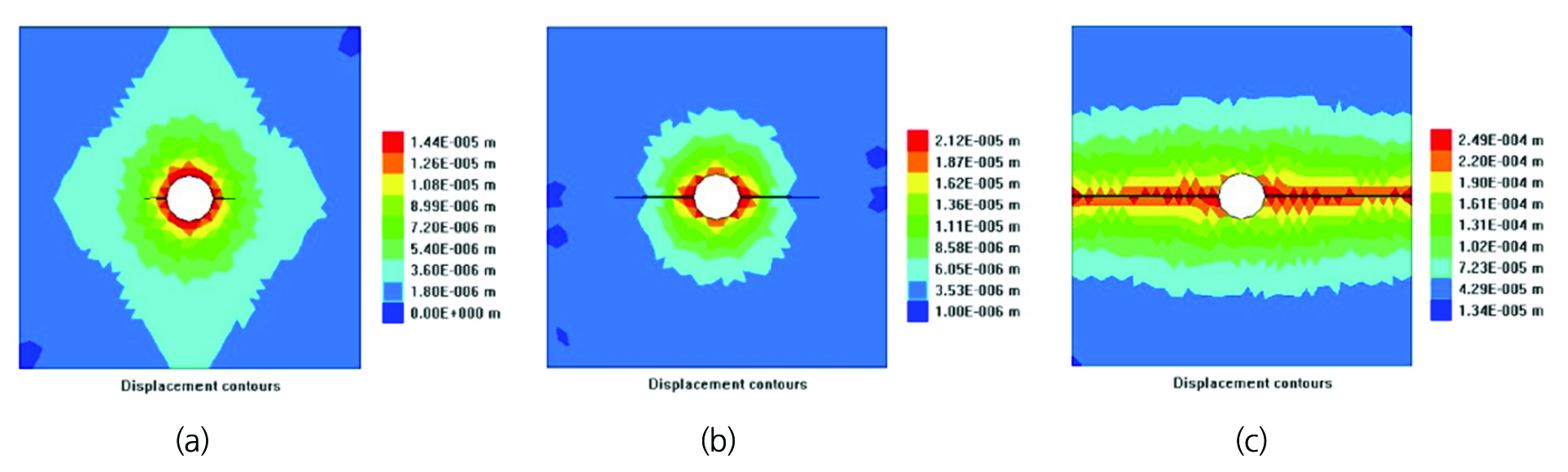
Fig. 11

Displacement contours during hydro-mechanical fracturing simulations based on DDARF methods: (a) 30 steps, (b) 50 steps, and (c) 100 steps (Jiao et al., 2015)

Morgan and Aral(2015)은 앞서 Ben et al.(2013)에 의해 제시된 HFDDA 기법의 유체, 접촉면 및 복합거동 해석 알고리즘을 개선하여 정확도 및 안정성을 높이고자 하였다. 개선된 HFDDA의 수리-역학적 복합거동 해석 알고리즘은 유체 압력에 의한 불연속면의 변위에 관한 정해(Sneddon and Lowengrub, 1969)와 수압파쇄 조건에서 불연속면의 전파를 설명하는 KGD(Kristianovich-Geertsma-de Klerk) 모델(Khristianovich and Zheltov, 1955) 변형 및 전파와 정해를 바탕으로 검증되었다.

Choo et al.(2016)은 DDA 블록 모델에 유한요소법을 적용하여 블록 내 역학적 해석 성능을 높이고자 하였고, 구축된 DDA-FEM 해석모델을 활용하여 시추공 모델에서의 수압파쇄 실험을 모사하였다. DDA-FEM 해석기법에서는 FEM 기반 역학적 해석에 따른 높은 역학적 해석 효율과 DDA 해석기법을 바탕으로 한 폭넓은 단위시간 선택으로, 수리-역학적 복합거동 해석의 효율 및 정확성을 증대시켰다. 구축한 DDA-FEM 해석기법을 활용하여 불연속면이 존재하는 암반에서의 수압파쇄 양상을 유체 주입 속도에 따라서 확인하였으며, 이 과정에서 다양한 단위시간을 선택할 수 있음을 증명하였다.

3.4 FRACOD

FRACOD(FRActure propagation CODe)는 Shen and Stephansson(1994)의 균열 전파 양상에 관련된 이론인 G-crtierion을 반영하여 균열 전파 모델링에 특화된 변위불연속법(Displacement Discontinuity Method, DDM) 수치해석 프로그램이다(Shen, 2010). 변위불연속법은 경계요소법(Boundary Element Method, BEM) 중 하나로, 2차원 모델 내 불연속면을 나타내는 변위불연속요소(displacement discontinuity components)를 유한한 선으로 표현하여 변위불연속요소에 대한 정해를 바탕으로 수치해석을 수행한다(Fig. 12). 변위불연속요소의 집합을 통해 불연속면을 나타내며, 변형률 기반 균열 전파 이론과 에너지 기반 균열 전파 이론을 바탕으로 mode I 및 mode II 균열 생성 및 전파를 새로운 변위불연속요소의 생성으로 모사할 수 있다. 역학적으로 검증이 완료된 FRACOD를 발전시켜 Shi et al.(2014)은 3차원 균열 성장 모델을 반영하여 3차원 변위불연속법 기반 균열 전파 수치해석 프로그램 FRACOD3D를 개발 및 상용화하였다.

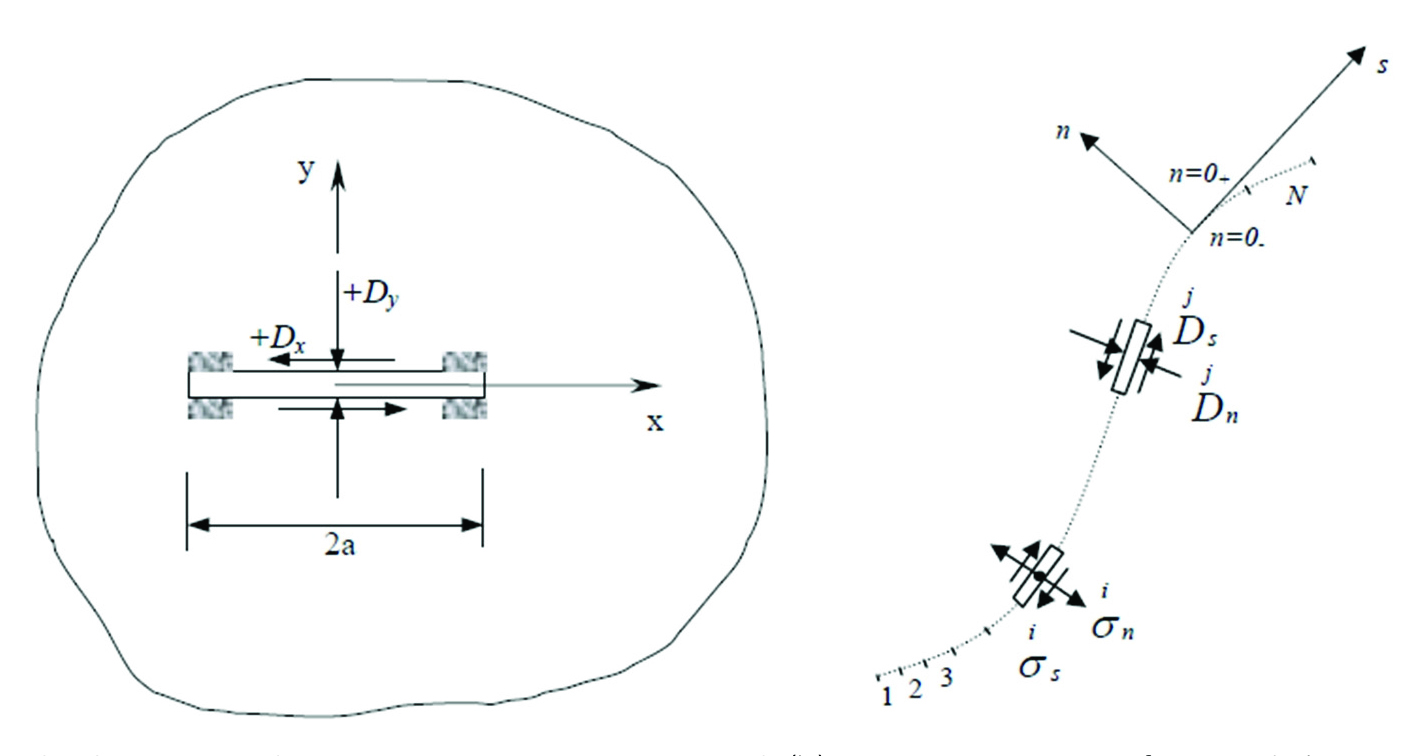
Fig. 12

(a) Constant displacement discontinuity components and (b) representations of a crack by N element displacement discontinuities in FRACOD (Shen, 2002)

Shen(2010)은 FRACOD 내에 구현된 변위불연속요소를 유체 유동 경로로 설정하여 수리학적 해석기법을 제시하였고 (Fig. 13), 역학적 해석을 통해 도출된 변위불연속요소의 간극을 삼승법칙을 통해 투수량계수로 변환하여 압력 구배에 의해 유체 유동 경로를 따라 흐르는 유량을 계산한다. 새롭게 계산된 유체 압력 데이터를 기반으로 모델에 역학적 교란이 가해지고, 역학적 해석 결과에 따라 불연속면의 생성, 변형 및 전파 양상을 계산하여 새로운 유체 유동 경로를 수리학적 해석 알고리즘에 반영한다. 이러한 역학적 해석과 수리학적 해석의 반복을 통하여 균열암반에서의 수리-역학 복합거동을 구현할 수 있다.

Fig. 13

Domain division for fluid flow in FRACOD (Shen, 2010)

FRACOD는 불연속면의 생성 및 전파를 구현하는 데에 특화된 만큼, 수리-역학적으로 균열을 생성하는 수압파쇄의 모델링이 주로 이루어졌다. Xie et al.(2016)은 FRACOD 내에 구현된 수리-역학 해석 알고리즘을 활용한 수압파쇄 해석을 위해 2차원 암반 모델 내에 시추공 및 불연속면을 구축하였다. FRACOD 내 수리-역학 해석 알고리즘의 검증을 위해 KGD 모델을 모사하였으며, 시간에 따른 균열 전파 양상 및 수리학적 반응을 비교하여 검증하였다. Fig. 14(a)은 FRACOD를 바탕으로 구축한 시추공 및 균열 모델로, 수압파쇄를 통한 균열 전파 과정에서 기존에 존재하는 균열(pre-existing fracture)과의 상호작용을 확인하고자 하였다. 2초간의 유체 주입 결과 Fig. 14(b)와 같이 균열이 연결되었으며, 유체 압력에 의한 간극의 열림 현상도 관측되었다.

Kim et al.(2011)은 FRACOD 내에 양해법을 기반으로 한 수리역학 복합거동 해석 모듈과 가상열원법 및 시간전진기법을 활용한 열역학 복합거동 해석 모듈을 각각 추가하여 검증하고자 하였다. 수리역학 복합거동 해석 모듈에 대한 검증을 위해 두 시추공 사이를 연결하는 균열망에서의 정상상태(steady-state) 유체유동을 확인하였고, 유체 주입 이후 주입 압력에 의한 수직 및 전단 변형을 정해와 비교하였다. 또한 FRACOD 내에서 구현 가능한 균열 전파 거동 해석 기법을 바탕으로 단일 시추공 수압파쇄 모델을 구축하여 유체 주입 압력에 의한 균열 전파 양상을 검토하였다.

Janiszewski et al.(2019)는 암반 내 자연균열에 수압파쇄를 통해 연결도를 상승시키는 과업을 FRACOD 내 수리-역학 복합거동 해석 알고리즘을 활용하여 모사하고자 하였다. 자연 균열을 내포하는 암반 모델을 구축하고, 수압파쇄를 진행하였을 때 자연균열의 각도 및 균열의 수리-역학적 특성에 따른 유체 유동을 관측하였다. 수압파쇄 이후에 균열은 인장파괴와 전단 미끄러짐이 복합적으로 발생하며 연결되었고, 연결된 균열을 따라 유체 압력이 전달된 것을 확인할 수 있었다(Fig. 15). 이처럼 FRACOD 내 수리-역학 복합거동 해석 알고리즘은 균열의 생성, 전파, 변형, 미끄러짐을 모두 고려하여 역학적 해석 결과에 따른 균열의 수리학적 특성 변화를 자세하게 모사할 수 있음을 확인하였다.

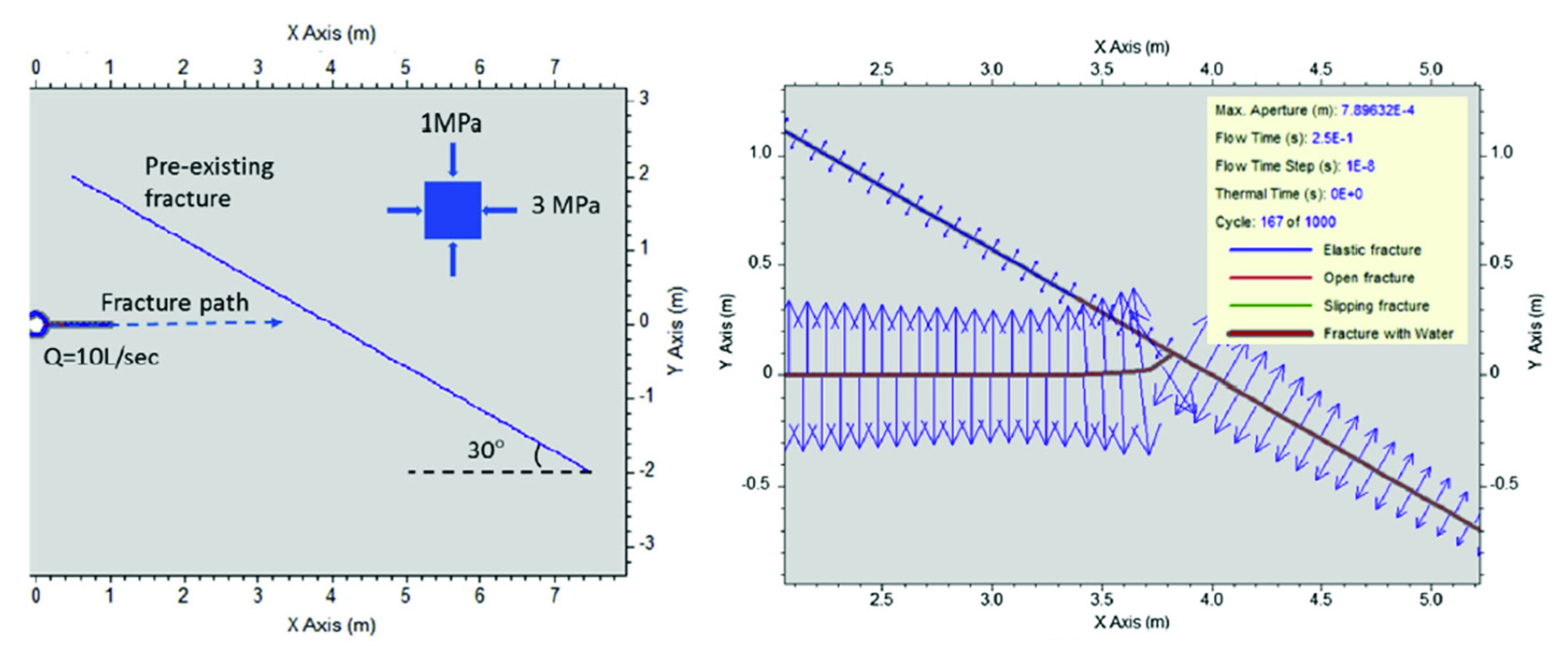
Fig. 14

(a) FRACOD model for simulation hydraulic fracture diversion and (b) hydraulic aperture distribution after two second injection (Xie et al., 2016)

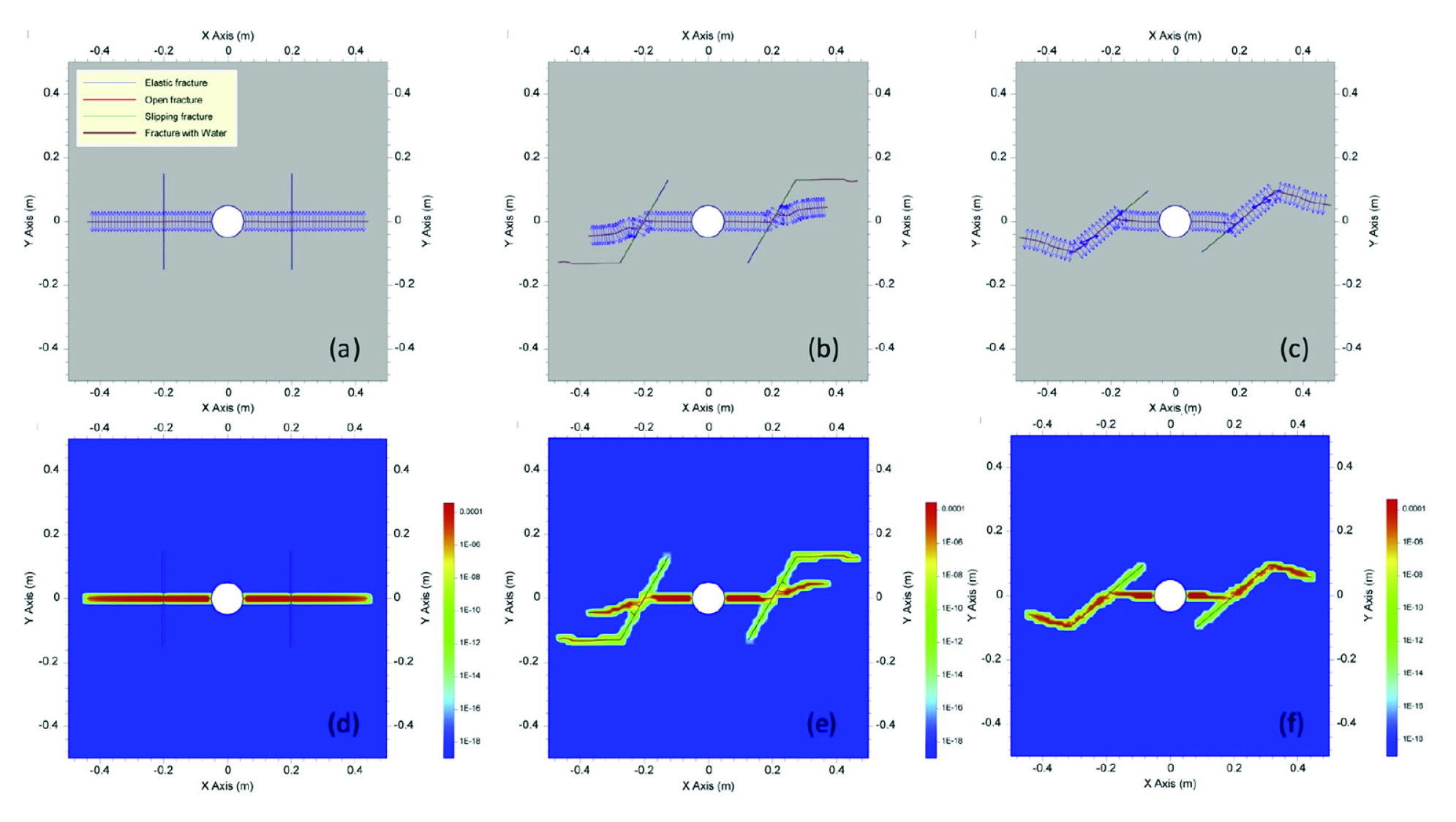
Fig. 15

Distributions of fluid pressure (a-c) and hydraulic conductivity (d-f) by approach angles of natural fractures (Janiszewski et al., 2019)

3.5 TOUGH-UDEC

앞서 소개한 불연속체 기반 해석 프로그램 UDEC은 균열상의 유체 유동을 고려하여 균열암반에서의 열-수리-역학적 복합거동을 모사할 수 있다. 하지만 고준위방사성폐기물 심층처분, 이산화탄소지중저장, 심부지열에너지개발 등과 같이 실제 균열암반에서의 거동 해석을 요하는 분야에서는 다상(multi-phase) 및 다성분(multi-component)의 유체 유동과 더불어 암석 및 균열에서의 열-수리-역학-화학적 복합거동 상호작용에 대한 구체적인 해석이 필요하다. Lee et al.(2019)은 UDEC이 균열에서의 수리학적 거동만 모사할 수 있고, 모사할 수 있는 수리학적 거동 특성이 제한되었다는 단점을 보완하기 위하여, 다상, 다중 유체의 열-수리 복합거동 해석이 가능한 TOUGH2(Pruess et al., 2012)와 결합한 TOUGH-UDEC 시뮬레이터를 개발하였다.

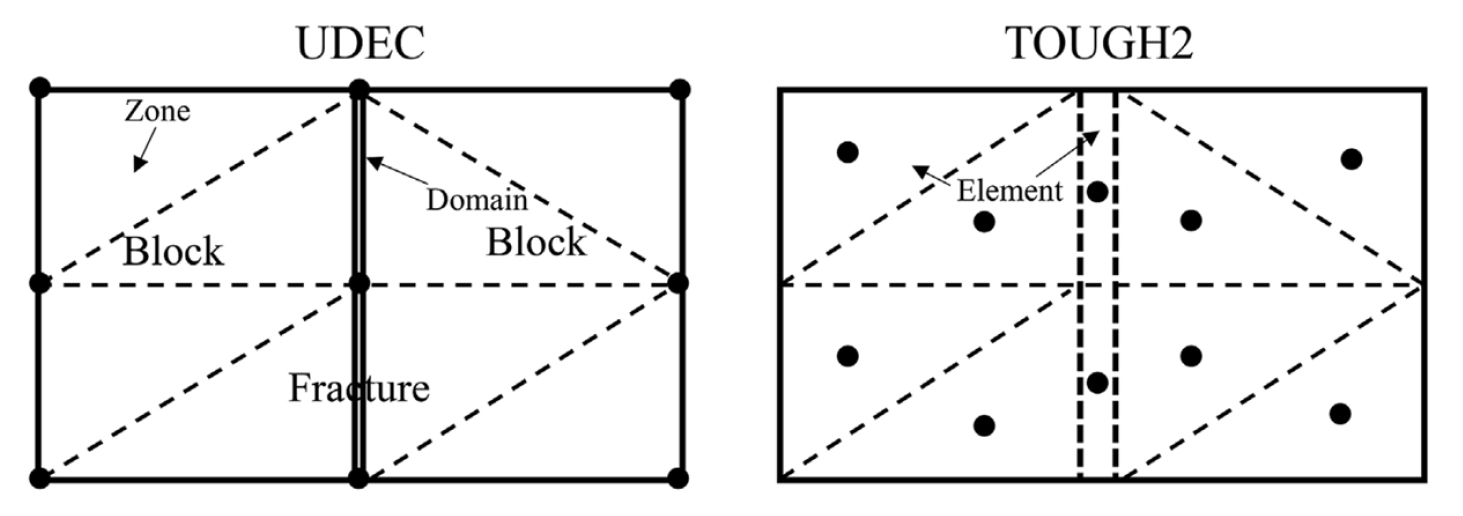
TOUGH2와 UDEC의 연동해석을 수행하기 위해 두 코드에서 암반과 균열을 구성하는 메쉬의 형상과 순서가 같아야 한다. 이를 위해 MATLAB 코드 기반의 UDEC에서 구성된 메쉬를 기반으로 TOUGH2 메쉬를 생성하는 알고리즘을 이용한다. TOUGH2의 메쉬는 요소의 중심에 하나의 절점이 위치하는 유한체적요소로 구성되고, UDEC의 메쉬는 암반 블록을 구성하는 영역(zone)과 균열을 구성하는 도메인(domain)으로 나뉘며, 절점이 암반 블록 영역의 모서리에 위치한다(Fig. 16). 도메인의 폭은 균열 간극 크기를 나타내므로 암반 블록 영역의 크기보다 상대적으로 매우 작아 TOUGH2에서의 유체 유동 및 열해석 시 수렴도에 영향을 주어 계산간격(time step)을 감소시킨다. 이러한 영향을 감소시키기 위해 TOUGH2의 균열 메쉬는 등가투수계수(k_c) 및 유효공극률(n_c)을 이용하여 UDEC의 도메인 간극(e)보다는 더 큰 두께(b)를 갖는 다공성 매질로 나타내었다(식 15, 16).

Fig. 16

Schematic view of basic mesh structures in UDEC and TOUGH2 (Lee et al., 2019)

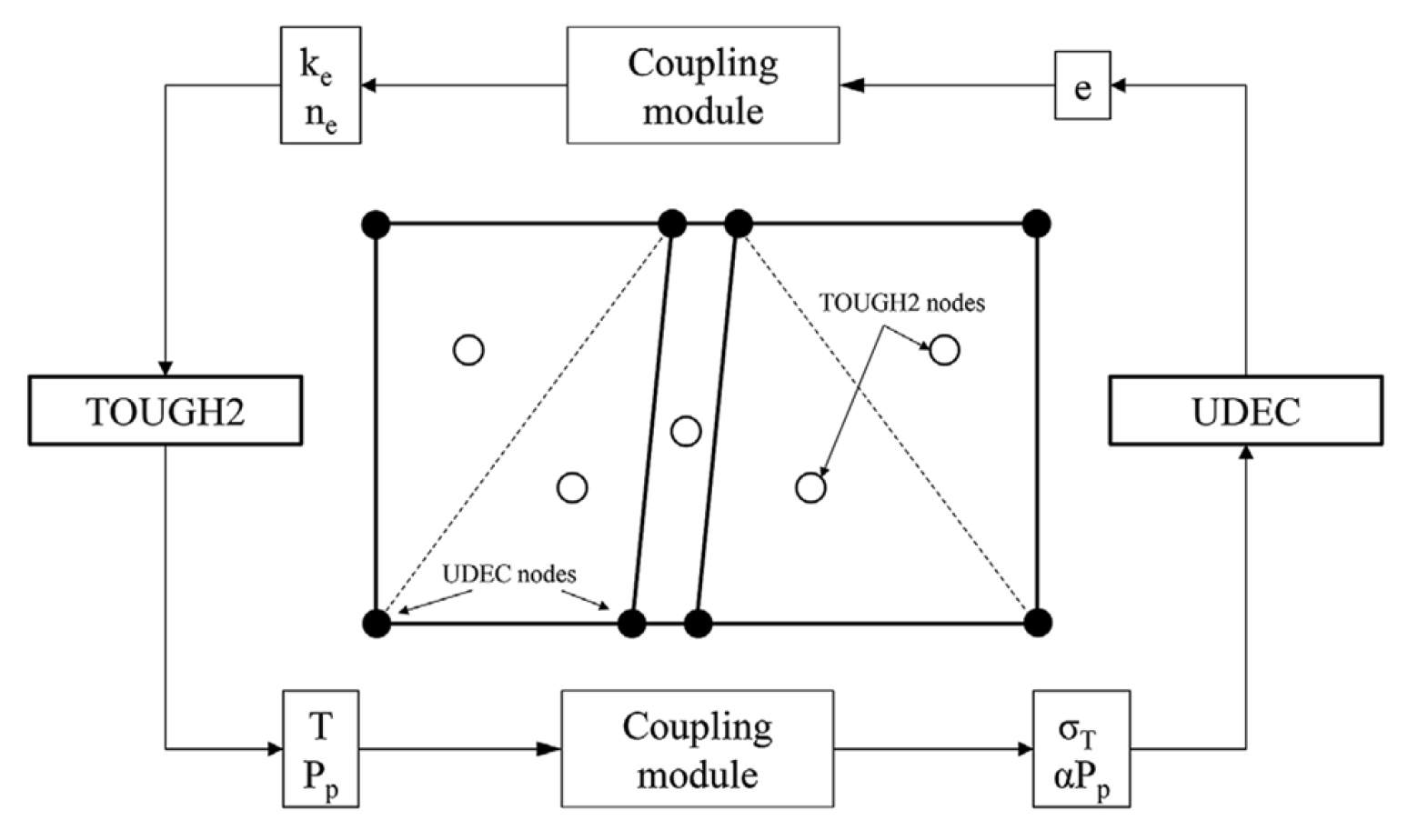
Fig. 17은 TOUGH-UDEC 시뮬레이터의 연동해석 알고리즘 모식도이다. TOUGH2에서 열 및 수리 해석을 수행한 후, 온도 및 압력 자료를 UDEC으로 전달한다. 압력은 암반 블록 영역과 균열 도메인의 중심 절점에 저장 되고, 온도는 중심으로부터의 거리를 고려하여 모서리에 저장된다. UDEC에서 역학적 해석을 수행하여 계산된 간극 변화를 TOUGH2로 전달하고 TOUGH2에서 간극 변화를 등가투수계수 및 유효공극률로 환산하여 유체 유동 해석을 수행한다. 계산간격은 TOUGH2에 의해 결정되며, 지정된 해석기간동안 이러한 명시적 연계 해석법(explicit sequential scheme)을 매 계산간격마다 반복하여 해석을 수행한다.

Fig. 17

A flow diagram of the TOUGH-UDEC coupling procedure (Lee et al., 2019)

Lee et al.(2019)은 TOUGH-UDEC 시뮬레이터를 이용하여 심부 염수층 내 이산화탄소 지중저장 및 단층 거동으로 인한 누출 해석을 수행하였다. 덮개암 내 단층의 전단 미끄러짐에 의한 간극 변화를 확인하기 위해 2차원 불연속체 모델을 구축하였다. 이산화탄소가 사암층의 하부에 주입 되고, 사암층 상, 하부에는 투수계수가 낮은 덮개암 및 기저암이 위치하고 있다. 구축된 단층모델 내 단층의 마찰각에 변화를 주어가며 이산화탄소 주입에 따른 단층 거동 및 이산화탄소 누출 여부를 확인하고자 하였다. 20°의 마찰각을 갖는 단층 모델에서 이산화탄소의 주입에 따라 전단 미끄러짐이 발생하였고, 전단 팽창으로 인한 단층 투수계수 증가가 이산화탄소의 누출을 야기하는 결과가 도출되었다(Fig. 18).

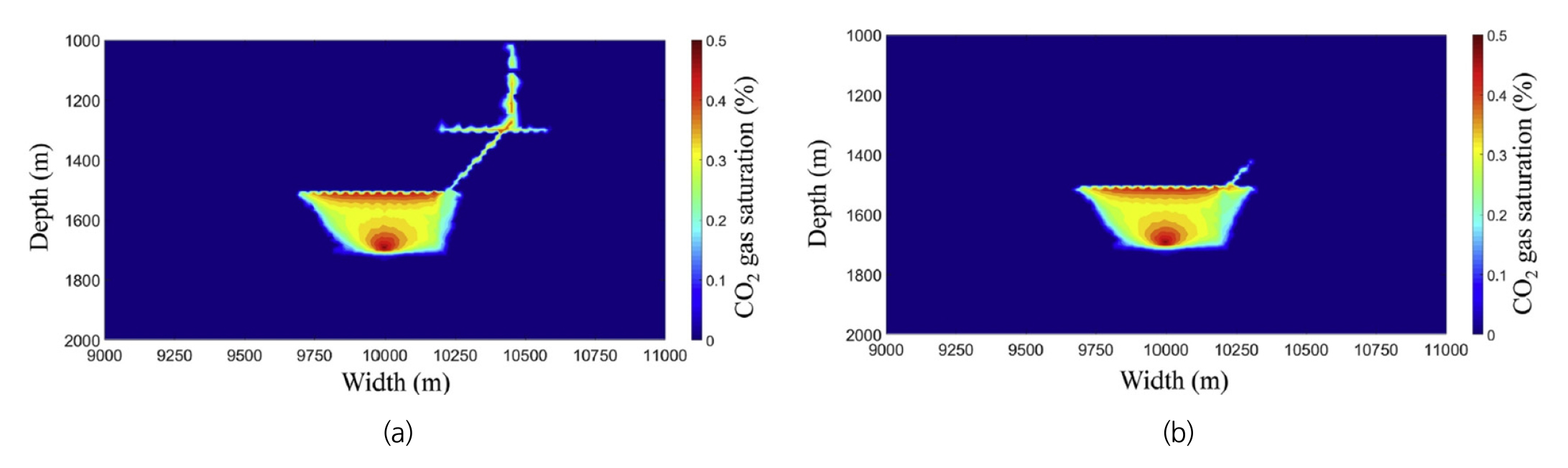
Fig. 18

CO₂ gas saturation contours on model with (a) 20° and (b) 40° friction angles after two years of injection (Lee et al., 2019)

Zareidarmiyan et al.(2020)은 균열을 포함한 저류층 내 유체 주입 시 발생하는 열-수리-역학적 복합거동을 TOUGH-UDEC과 유한요소법 기반의 CODE_BRIGHT(Olivella et al., 1996)로 해석한 결과를 비교하였다. 단일한 수평 균열을 포함한 저류층 경계부로 유체를 주입하였을 때의 균열에서의 공극압 및 간극 분포를 TOUGH-UDEC(TU) 및 CODE_BRIGHT(CB)의 수치해석 결과와 Wijesinghe(1986)의 준정해(semi-analytic solution)와 비교하였다. 공극압 및 간극은 주입점으로부터의 거리 및 시간에 따라 점차 증가하는 경향을 나타내고 이는 준정해와 거의 일치하였다(Fig. 19). 반면, 저류층 내 다수의 균열이 존재하는 경우 TOUGH-UDEC과 CODE_BRIGHT에서 유체 주입에 의한 압력 변화가 다르게 나타났다. TOUGH- UDEC은 균열 강성을 이용해 균열의 거동을 명시적으로 모사하지만, CODE_BRIGHT는 등가(equivalent) 탄성계수 및 포아송비를 이용하여 균열의 거동을 모사한다는 차이가 있다. 또한, CODE_BRIGHT는 수리-역학 복합거동 해석 시 완전연동 방식을 이용하여 저류층에서 순간적으로 공극압이 증가하는 스켐프튼(Skempton) 효과를 고려할 수 있으나 TOUGH-UDEC은 순차적 연동 방식을 이용하므로 스켐프튼 효과를 고려하지 못한다는 특징이 확인되었다.

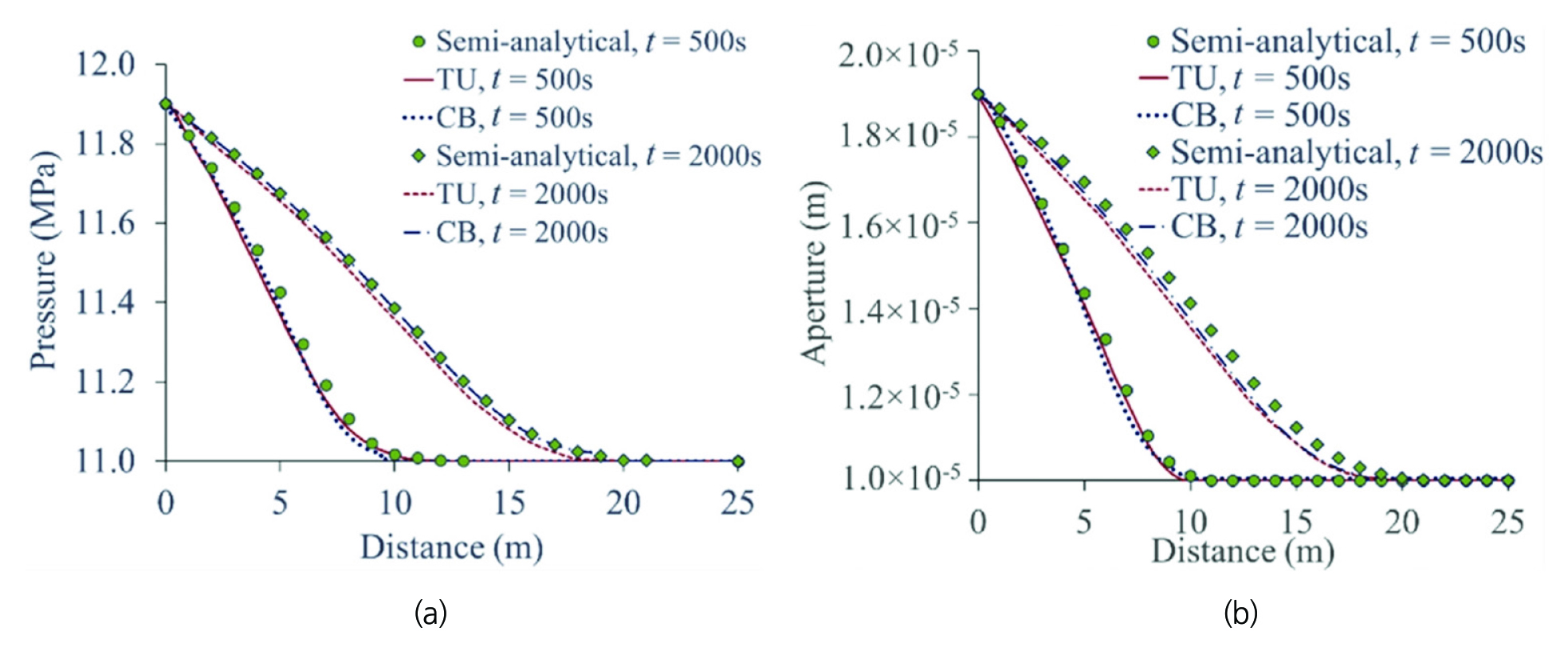
Fig. 19

(a) Pressure and (b) aperture distributions along the fracture for the semi-analytical solution and numerical results after 500 seconds and 2,000 seconds of water injection (Zareidarmiyan et al., 2020)

4. 결 론

고준위방사성폐기물 심층처분시스템 내 천연방벽은 방사성핵종 누출을 방지 및 지연하기 위한 수리학적 성능을 갖춰야 한다. 결정질 암반의 경우 암석 자체의 낮은 투수계수 때문에 수리학적 성능이 불연속면의 존재 및 변형에 따라 결정된다. 불연속체 기반 해석기법은 결정질 암반 내 여러 개의 불연속면을 구현하는 데에 특화되어있고, 불연속체의 생성, 전파, 변형, 미끄러짐 등의 자세한 역학적 거동을 모사할 수 있다. 블록 및 입자와 불연속면의 개별적인 거동을 바탕으로 전체 암반에 대한 역학적 해석을 수행할 수 있으며, 불연속면에서의 역학적 특성을 자유롭게 선택할 수 있어 넓은 분야로의 적용성을 갖고 있다. 불연속체 기반 해석기법은 역학적 해석에 초점을 맞추어 개발되었지만, 일부 프로그램에서는 수리학적 해석 모듈을 개발하여 불연속체에서의 수리-역학 복합거동 해석을 제공하였다. UDEC, 3DEC, DDA와 같은 블록 기반 불연속체 해석모델의 경우에는 일반적으로 불연속체 상에서의 유체 유동을 바탕으로 수리-역학적 복합거동 해석이 수행되었고, PFC와 같은 입자 기반 불연속체 해석모델은 모델 전체에 대한 유체 유동을 기반으로 복합거동 해석을 수행하였다. UDEC의 경우 TOUGH2 프로그램과 결합함으로써 블록 및 불연속체 전체에 대한 다상·다중 유체 유동 복합거동 해석을 제공하였다. 불연속체 기반 수리-역학 복합거동 해석기법은 주로 균열암반 및 단층에의 유체를 주입하는 수압파쇄, 심부지열에너지개발, 이산화탄소지중저장 등의 분야에 활용되었고, 유체 주입에 따른 불연속면의 생성, 전파, 변형, 미끄러짐 거동 분석을 중점적으로 수치해석이 수행되었다.

고준위방사성폐기물 심층처분시스템의 성능평가를 위해서는 수리-역학 복합거동뿐만 아니라 열 및 화학적 영향 또한 검토되어야 한다. 현재까지 개발된 불연속체 기반 수리-역학 복합거동 해석기법의 경우 대부분이 2차원 해석에 국한되어 있거나, 수리학적 해석 성능이 떨어지고, 불연속면에서의 유체 유동만 고려되거나, 다상·다중 유체 유동과 같은 복잡한 수리학적 해석을 지원하지 않는 등의 한계점을 갖고 있어 처분시스템 모델링에는 미흡한 실정이다. 또한, 열 및 화학적 복합거동 해석을 위해서는 더 폭넓은 적용성을 가진 해석기법이 필요하다. 따라서 고준위방사성폐기물 심층처분시스템 모델링을 위한 불연속체 기반 열-수리-역학-화학 복합거동 해석기법의 개발이 필요하고, 본 기술보고에서 검토한 다양한 복합거동 해석기법의 개념 및 알고리즘을 바탕으로 향후 더 정확하고 신뢰할 수 있는 복합거동 해석기법을 개발할 수 있을 것으로 전망한다.