A Comparative Study of Simplified Probabilistic Analysis Methods for Plane Failure of Rock Slope

Youngmin Kim

doi:10.7474/TUS.2021.31.5.360

Preview

Original Article

Tunnel and Underground Space. 31 October 2021. 360-373
https://doi.org/10.7474/TUS.2021.31.5.360

A Comparative Study of Simplified Probabilistic Analysis Methods for Plane Failure of Rock Slope

암반사면의 평면파괴해석을 위한 간이 확률론적 해석 비교연구

Youngmin Kim¹^*

김 영민¹^*

¹Professor, Dept. of Civil & Environmental Engineering, Jeonju University

¹전주대학교 토목환경공학과 교수

^{*Corresponding Author}

ABSTRACT

Many sources of uncertainty exist in geotechnical analysis ranging from the material parameters to the sampling and testing techniques. The conventional deterministic stability analysis of a plane failure in rock slope produce a safety factor but not a probability of failure or reliability index. In the conventional slope stability analysis by evaluating the ground uncertainty as an overall safety factor, it is difficult to evaluate the stability of the realistic rock slope in detail. This paper reviews some established probabilistic analysis techniques, such as the MCS, FOSM, PEM, Taylor Series as applied to plane failure of rock slopes in detail. While the Monte – Carlo methods leads to the most accurate calculation of the probability of safety, this method is too time consuming. Therefore, the simplified probability methods could be alternatives to the MCS. In this study, using these simple probability methods, the failure probability estimation of a plane failure in rock slope is presented.

Keywords

Plane failure

Safety factor

Reliability index

Failure probability

Simplified probabilistic analysis

지반공학 분석에는 재료정수의 샘플링 및 실험기술에 이르기까지 많은 불확실성의 원인이 존재한다. 암반사면의 평면파괴에 대한 기존의 결정론적 안정성 분석은 안전율은 계산하지만, 파괴확률이나 신뢰지수를 고려하지 않는다. 기존의 사면안정해석에서는 지반의 불확실성을 전체적 안전율로 평가하여 현실적인 암반사면의 안정성을 자세히 평가하기가 힘들다. 본 논문에서는 암석사면의 평면파괴에 적용되는 MCS, FOSM, PEM, Taylor Series와 같은 기존의 확률론적 분석기법을 자세히 검토한다. 몬테카를로 방법(MCS)은 가장 정확한 확률론적 안전율을 계산한다. 그러나 이 방법은 시간이 많이 걸리는 문제가 발생되므로 간이 확률론적 방법은 MCS에 대한 대안이 될 수 있다. 이 연구에서는 간이 확률론적 방법을 사용하여 암반사면의 평면파괴에 대한 확률분석을 제시하였다.

키워드

평면파괴

안전율

신뢰지수

파괴확률

간이 확률론적 해석

MAIN

1. 서 론
2. 확률론적 해석방법
2.1 확률변수 특성 값
2.2 확률분포
2.3 파괴확률, 신뢰지수
2.4 FOSM
2.5 PEM
2.6 테일러급수 근사법
2.7 몬테카를로 모사법(Monte Carlo Simulaiton)
3. 암반사면의 평면파괴 안정해석
3.1 인장 균열이 없는 경우
3.2 인장 균열이 있는 경우
4. 평면파괴에 대한 확률특성 분석
4.1 민감도 분석
4.2 모형 1 경우
4.3 모형 2 경우
5. 결 론

1. 서 론

전통적인 암반사면의 안전율은 지반의 각 설계정수의 평균값에 해당되는 값을 대표 값으로 간주하여 사면의 안전율을 하나의 값으로 평가하는 결정론적 방법(deterministic analysis)으로 구한다(김승곤 외, 2008). 하지만, 지반의 강도정수는 위치 및 실험방법에 따라서 변동이 있는 불확실한 값으로 변동성을 고려하는 확률해석(probabilistic analysis)이 필요한 변수이다. 이러한 확률론적 해석은 각 변수에 대한 불확실성(평균, 표준편차, 확률분포)을 고려하여 평가할 수 있고, 사면안전율에 대한 파괴확률(failure probability) 및 신뢰지수(reliability index)를 평가할 수 있어 합리적인 설계가 가능하다(윤우현과 천병식, 2003, Park and Baek, 2007). 사면의 안정성에 대한 확률해석은 정밀확률해석에 해당되는 MCS(Monte Carlo Simulation), 간이 확률 해석에 해당되는 FOSM(First Order Second Moment), PEM(Point Estimate Method), 테일러 급수법(Taylor series method) 등이 사용되고 있다(Duncan, 2000, Griffiths et al., 2002)

그러나 이러한 확률론적 해석법은 기존의 방법에 비하여 이론상 개념과 용어가 익숙하지 않고, 많은 실험 데이터 및 더 많은 계산이 요구되는 관계로 실무에 많이 활용되지 못하고 있는 실정이다(배규진 외, 2002, 장연수 외, 2002, Schweiger et al., 2001). 본 논문에서는 지반의 불확실성을 고려한 암반사면의 평면파괴에 대한 사면안정성에 대하여, 보다 간편히 적용할 수 있는 기존의 제안된 간이 확률론적 해석법에 대하여 비교, 분석하였다.

2. 확률론적 해석방법

2.1 확률변수 특성 값

어떤 설계변수가 확률밀도 f_X(x)를 가진 확률변수(random variable) X로 가정하면, 확률론적 해석을 하기 위하여 평균값(μ_x), 표준편차(σ_x), 왜곡도(ν_x) 등의 확률변수 특성 값이 필요하다. 평균은 1차모멘트와 같고 다음과 같이 표현된다(Griffiths et al., 2002).

(1)

μ_{x} = E [X] = \int_{- \infty}^{\infty} x f_{X} (x) d x

분산은 2차모멘트로 다음과 같이 표현된다.

(2)

σ_{x}^{2} = V [X] = E [(X - μ_{x})^{2}] = \int_{- \infty}^{\infty} (x - μ_{x})^{2} f_{X} (x) d x

왜곡도는 3차모멘트로 다음과 같이 표현된다.

(3)

v_{x} = \frac{E [(X - μ_{x})^{3}]}{σ_{x}^{3}} = \frac{1}{σ_{x}^{3}} \int_{- \infty}^{\infty} (x - μ_{x})^{3} f_{X} (x) d x

2.2 확률분포

일반적으로 지반강도정수의 확률분포는 대수정규분포(log normal distribution)로 가정한다(Duncan, 2000). 어떤 지반강도정수 X의 평균값 μ_x, 표준편차 σ_x라고 하면, 대수정규분포는 lnX가 다음과 같은 정규분포로 표현된다.

(4)

f (X) = \frac{1}{\sqrt{2 π ζ}} e x p [- \frac{1}{2} {(\frac{\ln X - λ}{ζ})}^{2}]

여기서 $λ = E (l n X), ζ = \sqrt{V (l n X)}$

이러한 대수정규분포는 확률변수 값이 항상 양의 값이 되어야 정의되기 때문에 물리적인 변수 값이 양으로 정의되는 확률문제에 적용된다. 대수정규분포의 평균 λ, 표준편차 ζ는 다음과 같이 정규분포의 확률변수 X의 평균 μ_x, 표준편차 σ_x와 다음과 같이 연관되어 있다(Kamien, 1997).

(5)

ζ^{2} = l n (1 + C O V_{x}^{2}), C O V_{x} = \frac{σ_{x}}{μ_{x}}

(6)

λ = l n μ_{x} - \frac{1}{2} ζ^{2}

여기서 COV_x는 변동계수(coefficient of variance)이다.

2.3 파괴확률, 신뢰지수

사면의 안전율(F)은 파괴면에 발생되는 활동력(D)에 대한 저항력(R)의 비로 결정된다. 확률변수인 D, R의 차이를 다음과 같이 안전여유(Safety Margin)로 표시한다.

(7)

M = R - D

파괴는 M ＜ 0 일 때 발생되고 M ＞ 0 일 때는 발생되지 않은 것으로 볼 수 있다. 따라서 파괴확률은 아래와 같이 표현된다.

(8)

p_{f} = P (M ＜ 0) = Φ (- β) = 1 - Φ (β)

여기서 $β = \frac{E [M]}{\sqrt{V [M]}}$ 는 신뢰지수, Φ는 누적 정규분포함수(cumulative normal distribution function)이다.

신뢰지수는 표준편차로 정규화시킨 안전여유이다. 일반적으로 건설분야에서는 구조물의 파괴확률은 1/1000을 목표로 하여 설계한다. 또한 사면의 안전율이 대수정규분포를 가진다고 가정하면, 다음과 같이 안전율에 대한 신뢰지수를 바로 계산할 수 있다(Kamien, 1997).

(9)

β = \frac{E [M]}{\sqrt{V [M]}} = \frac{E [l n R - l n D]}{σ_{l n (R / D)}} = \frac{E [l n F]}{σ_{l n F}} = \frac{l n F - \frac{1}{2} l n (1 + C O V_{F}^{2})}{\sqrt{l n (1 + C O V_{F}^{2})}} = \frac{l n (\frac{F}{\sqrt{1 + C O V_{F}^{2}}})}{\sqrt{l n (1 + C O V_{F}^{2})}}

여기서 F는 평균 사면안전율, COV_F는 사면안전율에 대한 변동계수이다.

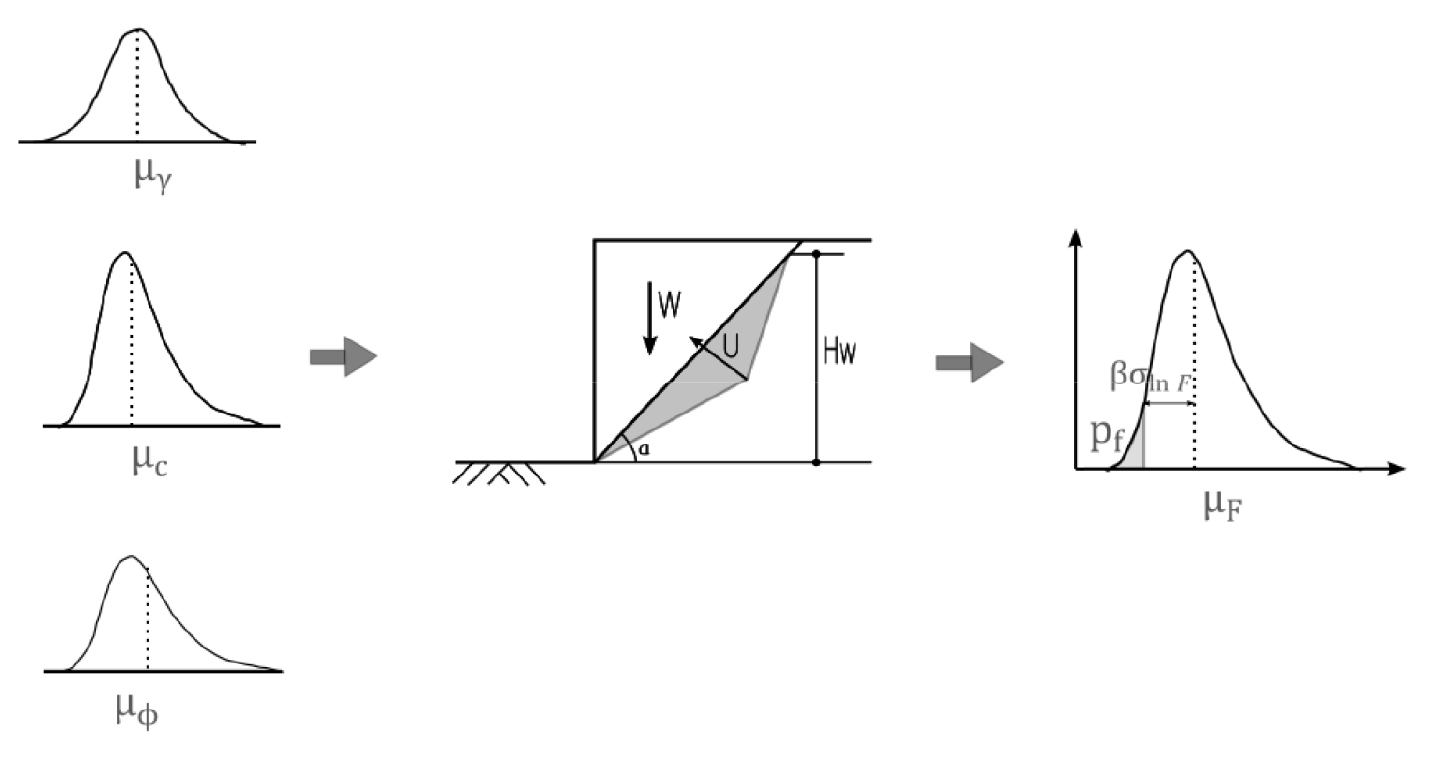
Fig. 1은 위의 과정을 간단히 그림으로 표현한 것으로 확률론적 해석과정의 개념을 보여준다.

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F1.jpg

Fig. 1

The probabilistic design model

2.4 FOSM

FOSM(First Order Second Moment)방법은 입력변수의 변동성 효과를 근사적으로 고려하는 확률론적 해석법이다. FOSM은 평가할 함수에 대한 근사식의 1차항만 포함하고 나머지 항을 무시하는 방법이다.

두 독립변수 X, Y를 가진 함수 f(X,Y)에 대한 평균값 근처에 대한 테일러 1차근사식으로 표현하면 다음과 같다(Griffiths et al., 2002).

(10)

f (X, Y) = f (μ_{x}, μ_{y}) + (X - μ_{x}) \frac{\partial f}{\partial x} + (Y - μ_{y}) \frac{\partial f}{\partial y}

함수에 대한 분산은

(11)

V [f (X, Y)] = V [(X - μ_{x}) \frac{\partial f}{\partial x} + (Y - μ_{y}) \frac{\partial f}{\partial y}]

(12)

V [f (X, Y)] = {(\frac{\partial f}{\partial x})}^{2} V [X] + {(\frac{\partial f}{\partial y})}^{2} V [Y] + 2 \frac{\partial f}{\partial x} \frac{\partial f}{\partial y} c o v (X, Y)

여기서 cov(X, Y)=E[(X-μ_x) (Y-μ_y)]은 공분산(covariance)이다.

만약에 X, Y 변수 간에 연관성이 없으면 함수 f(X,Y)에 대한 분산은 아래와 같이 표현된다.

(13)

V [f (X, Y)] = {(\frac{\partial f}{\partial x})}^{2} V [X] + {(\frac{\partial f}{\partial y})}^{2} V [Y]

2.5 PEM

점추정법(Point Estimate Method)은 확률해석의 평균, 표준편차, 왜곡도를 간편하게 고려하는 방법이다. 점추정법은 수치적분법에서 샘플점과 가중치를 구하여 계산하는 가중평균법과 유사하다. 점추정법의 계산과정은 다음과 같다(Griffiths et al., 2002).

1. 확률독립변수와 종속변수 간의 관계를 구한다. W=f(X, Y)

2. 다음과 같은 샘플점의 위치를 계산한다.

(14)

ζ_{x} + = \frac{v_{x}}{2} + {(1 + {(\frac{v_{x}}{2})}^{2})}^{1 / 2}, ζ_{x -} = ζ_{x +} - v_{x}

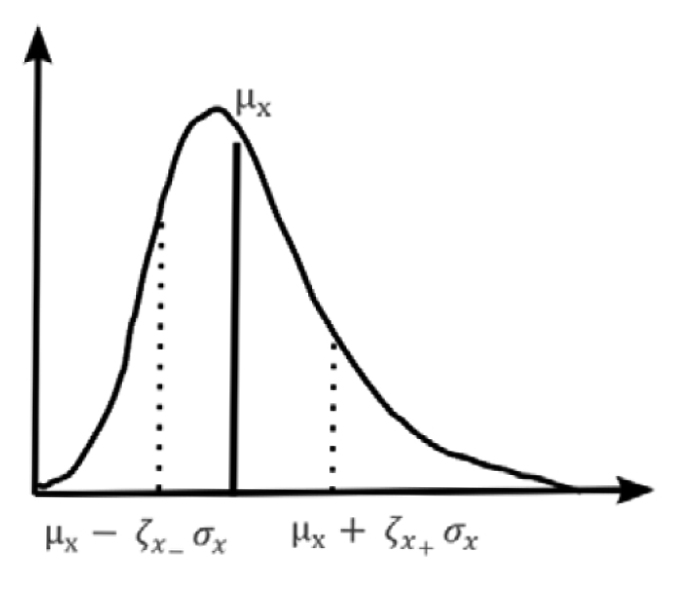
Fig. 2에서 보듯이 샘플점은 $μ_{x} + ζ_{x} + σ_{x}, μ_{x} - ζ_{x -} σ_{x}$ 이다.

3. 주어진 2ⁿ샘플점에서 가중치인 확률 Pi를 결정한다.

단일 확률변수 X에 대해서는 Pi는 아래와 같다.

(15)

P_{x +} = ζ_{x -} / (ζ_{x +} + ζ_{x -}), P_{x -} = 1 - P_{x +}

확률변수가 n개이고, 왜곡도가 없는 경우, Pi는 아래와 같다.

(16)

P_{s 1 s 2 . . . s n} = \frac{1}{2^{n}} (1 + \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} (s_{i} s_{j} ρ_{i j}))

여기서 s_i는 +-를 표시하는 부호이며, ρ_ij는 상관계수(correlation coefficient)이다.

4. 다음과 같이 확률변수의 평균(μ_w), 표준편차(σ_w), 왜곡도(v_w)를 구한다.

(17)

μ_{w} = E [W `] = Σ P_{i} W_{i}

(18)

σ_{w} = E [(W - μ_{w})^{2}] = Σ P_{i} W_{i}^{2} - μ_{w}^{2}

(19)

v_{x} = \frac{E [(W - μ_{w})^{3}]}{σ_{w}^{3}} = \frac{1}{σ_{w}^{3}} Σ P_{i} (W_{i} - μ_{x})^{3} = \frac{1}{σ_{w}^{3}} Σ P_{i} W_{i}^{3} - 3 μ_{w} P_{i} W_{i}^{2} + 2 μ_{w}^{3}

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F2.jpg

Fig. 2

PEM sampling points

2.6 테일러급수 근사법

테일러급수 근사법은 다음과 같은 방법으로 구한다(Duncan, 2000).

1. 입력변수의 평균값을 대표 값으로 가정하여 구하고자 하는 함수의 평균값(μ_F)을 구한다.

2. 각 확률변수의 표준편차를 가정하고, 변동성을 μ±σ으로 변화시키고 나머지 변수는 고정하여 함수의 변동성(∆F_i)을 구한다.

3. 위의 계산식에서는 2n+1번 계산이 필요하다. 여기서 n은 고려하는 확률변수의 개수다. 평균값(μ_F)을 구하기 위한 계산 1번과 변동성 계산을 위한 2n번의 계산이 필요하다.

4. 세 개의 확률변수를 가정하면 다음과 같은 방법으로 표준편차와 변동계수를 구한다.

(20)

σ_{F} = \sqrt{{(\frac{∆ F_{1}}{2})}^{2} + {(\frac{∆ F_{2}}{2})}^{2} + {(\frac{∆ F_{3}}{2})}^{2}}

(21)

C O V_{F} = \frac{σ_{F}}{μ_{F}}

여기서 σ_F는 사면안전율의 표준편차, COV_F는 사면안전율 변동계수이다.

2.7 몬테카를로 모사법(Monte Carlo Simulaiton)

몬테카를로 모사법(MSC)은 입력변수에 대하여 각각의 지정된 확률분포를 가지는 난수를 발생시켜, 구하고자 하는 함수를 반복적으로 계산을 수행하여 결과를 얻는 수치해석법이다. 수치해석 과정의 반복 수행으로부터 얻어진 결과는 물리적인 경험으로부터 관측된 표본과 유사한 결과를 얻을 수 있게 한다.

3. 암반사면의 평면파괴 안정해석

암반사면해석에서 사면의 안전율은 한계평형해석법(limit equilibrium method)으로 계산하는 경우가 많다. 한계평형해석법은 파괴활동면을 가정하고, 파괴활동면에 작용하는 저항력 R에 대한 활동력 D의 비로 다음과 같이 안전율을 정의한다.

(22)

F = \frac{R (c, ϕ, γ)}{D (c, ϕ, γ)}

3.1 인장 균열이 없는 경우

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F3.jpg

Fig. 3

Plane failure without tension crack (model 1)

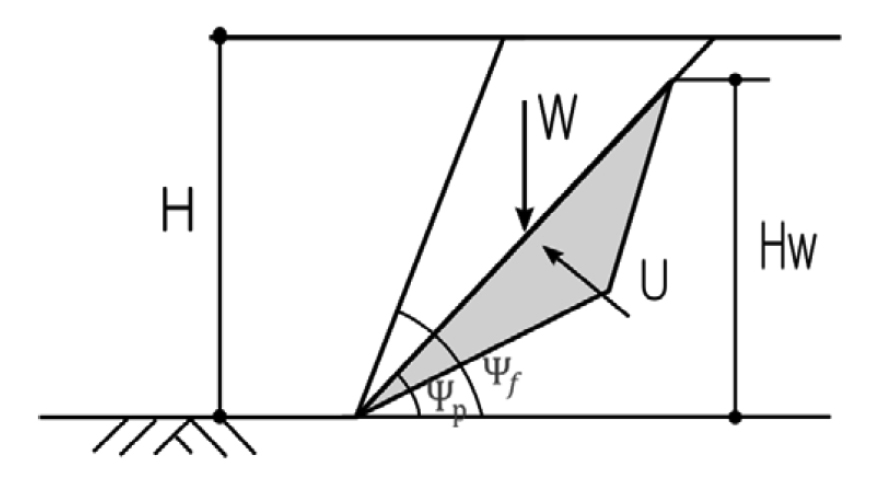
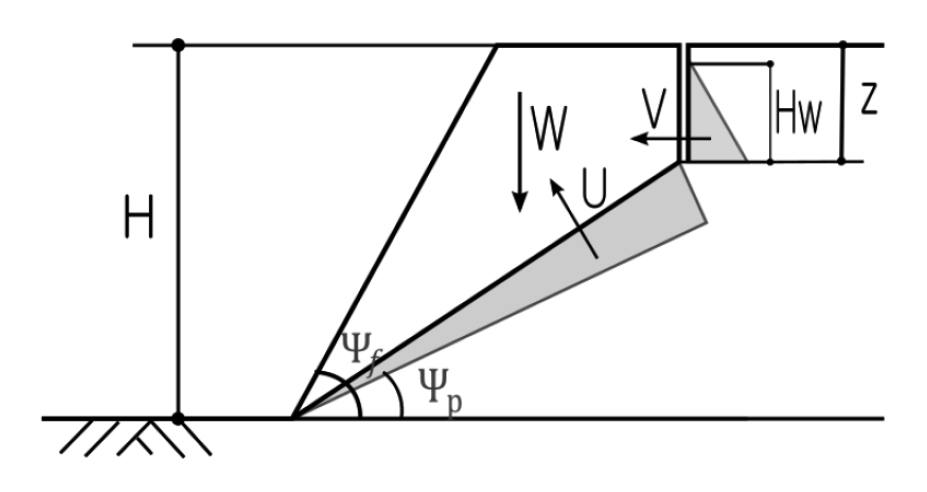
암반사면 평면파괴형태를 두 개의 모형으로 구분하였다. 첫 번째 모형은 인장균열이 없는 Fig. 3과 같은 형태의 모형이고, 두 번째 모형은 인장균열이 발생된 Fig. 4와 같은 경우이다(HoeK & Bray, 1981).

모형1에서의 사면의 안전율은 다음과 같이 정의된다.

(23)

F = \frac{c A + (W c o s Ψ_{p} - U) t a n ϕ}{W s i n Ψ_{p}}

여기서, c는 점착력, Ø는 마찰각, Ψ_p는 파괴활동면 각도, Ψ_f 사면의 기울기, Hw는 지하수위

A = H c s c ψ_{p}, W = \frac{1}{2} γ H^{2} c s c ψ_{p} c s c ψ_{f} s i n (ψ_{f} - ψ_{p}), U = \frac{1}{4} γ_{w} H_{w}^{2} c s c ψ_{p}

3.2 인장 균열이 있는 경우

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F4.jpg

Fig. 4

Plane failure with tension crack (model 2)

모형2에서의 사면의 안전율은 다음과 같이 정의된다.

(24)

F = \frac{c A + (W c o s Ψ_{p} - U - V s i n Ψ_{p}) t a n ϕ}{W s i n Ψ_{p} + V c o s Ψ_{p}}

여기서, z은 인장균열 깊이, $A = (H - z) \csc Ψ_{p}, W = \frac{1}{2} γ H^{2} ((1 - {(\frac{z}{H})}^{2}) c o t Ψ_{p} - c o t Ψ_{f})$

$U = \frac{1}{2} γ_{w} z_{w} A, V = \frac{1}{2} γ_{w} z_{w}^{2}$

4. 평면파괴에 대한 확률특성 분석

확률해석에 앞서 검토해야 할 것은 여러 입력변수 중 어떤 입력변수를 확률변수로 고려하여 해석에 사용할 것인가 하는 점이다. 본 연구에서는 사면안정의 설계변수인 지반재료정수를 확률변수로 선정하여 비교 분석하였다. 여기서 확률변수로 마찰각(Ø) 자체보다 마찰계수(tanØ)를 선택한 이유는 전단강도기준이 점착력과 마찰력성분으로 구성되기 때문이다. 이러한 지반재료정수의 변동계수(COVc,Ø,γ)는 0.03~0.5 범위에 있는 것으로 알려져 있다(Duncan, 2000).

4.1 민감도 분석

각 확률변수가 평면파괴 안전율에 미치는 영향을 조사하기 위하여, 모형 1에 대하여 각 확률변수의 변동성을 μ±σ으로 변화시키고 나머지 변수는 고정하여 발생되는 사면안전율의 변동(∆F=F₊‒F_‒)을 조사하였다. F_±는 입력한 확률변수의 변동을 표준편차만큼 발생시키고 계산한 사면안전율이다. 사면안정해석에 사용한 입력변수들의 값은 Table 1과 같다.

모형 1에 대한 평균값에 해당되는 결정론적 사면의 안전율은 F=1.7582로 평가되었다. 사면안전율에 대한 표준편차 및 변동계수는 Taylor 급수 근사법으로 분석하였다. 얻어진 계산결과를 살펴보면(Table 2 참조), 각 확률변수의 변동계수 0.1에 대하여 사면의 안전율의 변동계수(COV_F)가 0.0653, 0.0347, 0.0313으로 평가되어, 점착력> 마찰계수> 단위중량 순으로 영향을 크게 주는 것을 알 수 있다. 또한, 확률변수 중, 점착력, 마찰계수의 변동성 2개를 동시에 고려한 사면안전율의 변동계수는 0.074로 계산되었으며, 확률변수 세 개 모두를 고려한 사면안전율의 변동계수는 0.0803으로 입력확률변수의 변동성 0.1보다 다소 적게 평가되었다(Table 3 참조).

Table 1.

Input parameters on plane failure without tension (model 1)

Geometry of slope
Height H (m)	Face angle Ψ_f (°)	Failure plane angle Ψ_p (°)	Water level H_w (m)
30	50	30	30
Material parameters
Cohesion (kPa)	Friction angle (°)	Unit weight (kg/m³)	COV_c,tanØ,γ
100	35	2600	0.1

Table 2.

Taylor series reliability analysis for plane failure without tension crack (model 1)

Variable	Values	Factors of safety	∆F	Coefficient of variance for factor of safety (COV_F)
Cohesion (kPa)	90 110	F_‒=1.6433 F₊=1.8731	0.2297	0.0653
Friction coefficient	0.9 tan(35) 1.1 tan(35)	F_‒=1.6972 F₊=1.8192	0.1219	0.0347
Unit weight (kg/m³)	2340 2860	F_‒=1.8188 F₊=1.7086	-0.1102	0.0313

Table 3.

The result of COV on the plane failure without tension crack (model 1)

Conditions	Coefficient of variance for factor of safety (COV_F)
Cohesion, friction angle	0.0740
Unit weight, cohesion, friction angle	0.0803

또한, 정밀확률해석에 해당되는 MCS 해석에서는 반복횟수 N에 따른 민감도를 조사하기 위하여 반복횟수를 100~1000000으로 변경하여 사면안전율의 평균값을 조사하였다. 입력한 확률변수(점착력, 마찰계수, 단위중량)의 확률분포는 대수정규분포로 가정하였고, 반복횟수 N값이 100000이상이면 거의 차이가 없는 결과를 보여주었다(Table 4 참조). 이후 계산에서는 N값을 100000으로 지정하였다.

Table 4.

Average safety factor for plane failure without tension crack (model 1) using monte carlo simulation

N	100	1000	10000	100000	1000000
Average	1.7477	1.7485	1.7597	1.7585	1.7584
Absolute error (%)	0.5972	0.5532	0.0848	0.0178	0.0091

4.2 모형 1 경우

여러 확률론적 해석법에 따른 입력변수의 불확실성에 대하여 사면 안전율의 변동계수를 계산하기 위하여, 첫번째로 점착력, 마찰계수만 확률변수로 간주하여 입력 변동계수를 0.1~0.5범위에서 변화시키면서 사면안전율의 변동계수를 조사하였다.

Table 5의 해석결과를 보면, 입력한 변동성보다는 사면안전율에 대한 변동성이 다소 적게 평가되었으며, MCS와 간이 확률해석법(FOSM, PEM, Taylor series)들의 해석결과(안전율과 확률변수 간의 선형관계 경우)는 동일하였다.

Table 5.

COV of Safety factor using probabilistic methods (considering cohesion, coefficient of friction)

COV_c,tanØ	MCS	FOSM	PEM	Taylor Series
0.1	0.073923	0.073959	0.073959	0.073959
0.2	0.147934	0.147918	0.147918	0.147918
0.3	0.221892	0.221876	0.221876	0.221876
0.4	0.295507	0.295835	0.295835	0.295835
0.5	0.370213	0.369794	0.369794	0.369794

두 번째로, 점착력, 마찰계수, 단위중량 세 개 모두 확률변수로 고려하여 입력변수의 변동계수가 0.1~0.5까지의 변동에 따른 사면안전율의 미치는 변동계수를 계산하였다.

Table 6의 해석결과를 살펴보면, 확률변수 세 개를 고려한 경우가 확률변수 점착력, 마찰계수만 고려한 경우보다 사면안전율 변동이 다소 크게 평가되었으며, MCS와 간이 확률해석법(FOSM, PEM, Taylor series)들의 해석결과(안전율과 확률변수 간의 비선형관계 경우)는 다소 차이가 발생하였다. 또한, 간이 확률해석법 중 PEM 방법이 정밀한 확률해석법인 MCS 해석결과와 보다 유사한 결과를 나타낸다.

Table 6.

COV of Safety factor using probabilistic methods (considering cohesion, coefficient of friction, unit weight)

COV_c,tanØ,γ	MCS	FOSM	PEM	Taylor Series
0.1	0.080823	0.073959	0.081208	0.080323
0.2	0.165289	0.147918	0.167762	0.161419
0.3	0.257837	0.221876	0.262159	0.244310
0.4	0.361975	0.295835	0.363291	0.330664
0.5	0.488337	0.369794	0.467609	0.423693

PEM방법으로 계산한 모형1에 대한 사면 안전율분포를 정규분포로 가정한 경우와 대수정규분포로 가정한 경우에 따른 입력한 변동성에 대한 신뢰지수와 파괴확률은 Table 7과 같다.

Table 7.

Reliability index and failure probability for plane failure considering cohesion, coefficient of friction, unit weight

COV_c,tanØ,γ	Reliability index (β)		Failure probability (p_f)
COV_c,tanØ,γ	normal	log normal	normal	log normal
0.1	5.40E+00	7.08E+00	3.27E-08	6.96E-13
0.2	2.745667	3.622189	0.003019	0.000146
0.3	1.885082	2.514836	0.029709	0.005954
0.4	1.475623	2.005332	0.070022	0.022464
0.5	1.245907	1.742398	0.106399	0.040719

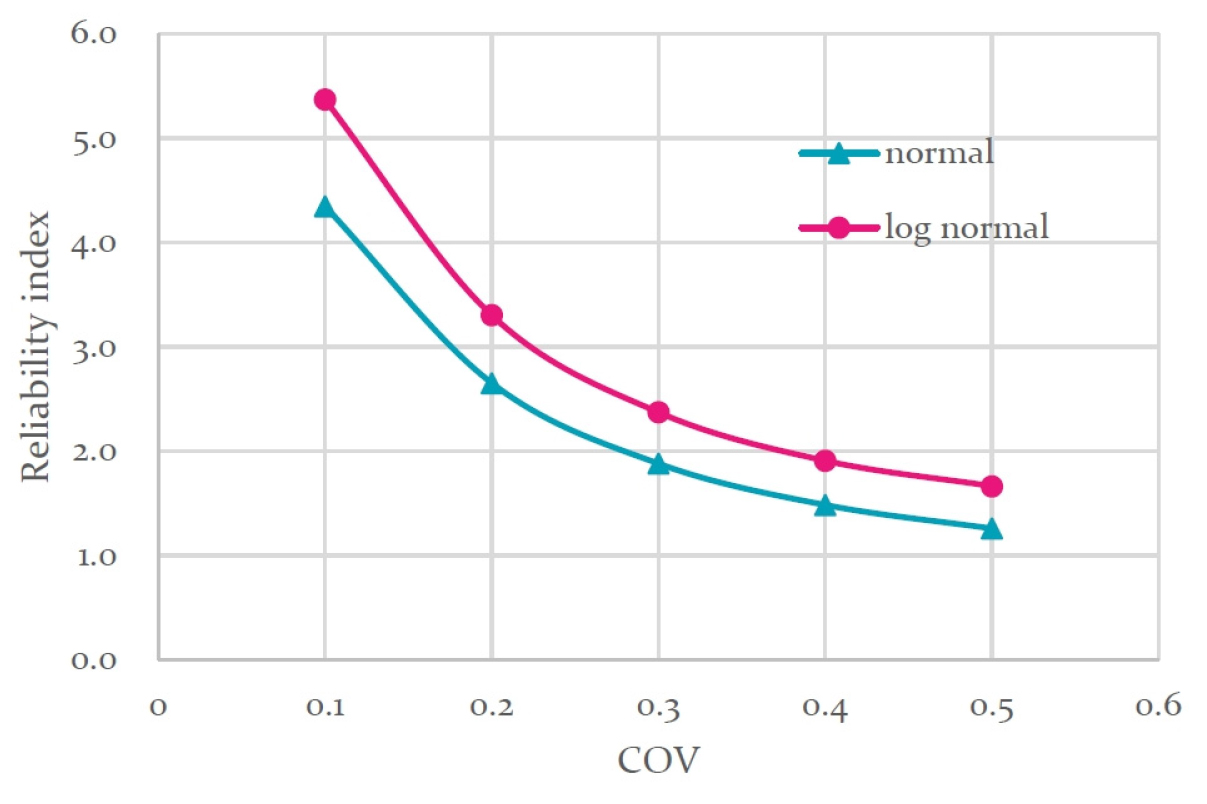
Table 7의 결과를 분석하여 보면, 입력한 변동성의 크기에 따라서 신뢰지수가 비례하여 감소하고, 파괴확률은 증가한다. 입력한 변동계수가 0.2보다 큰 경우는 결정론적 안정성(F>1.5)은 만족하나, 파괴확률은 0.001보다 커서 확률론적 안정성은 만족하지 못하는 결과를 보여주었다. 또한 대수정규분포로 가정한 경우가 정규분포로 가정한 경우보다 신뢰지수의 크기가 다소 크게 평가되는 경향을 보인다(Fig. 5 참조).

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F5.jpg

Fig. 5

Reliability index vs. COV

4.3 모형 2 경우

모형 2를 대상으로 입력변수의 불확실성을 고려한 확률론적 사면의 안전율을 계산하기 위하여 인장균열 수위를 10m로 고정하고, 점착력, 마찰계수, 단위중량을 확률변수로 간주하여 입력변수의 변동(0.1~0.5)에 따른 사면안전율의 변동계수를 계산하였다. 해석에 사용한 입력정수는 Table 8과 같다.

Table 8.

Input parameters on plane failure (model 2)

Geometry of slope
Height	Face angle	Failure plane angle	Tension crack	Water level
H (m)	Ψ_f (°)	Ψ_p (°)	z (m)	Hw (m)
30	50	30	10	10
Material parameters
Cohesion (KPa)	Friction angle (°)	Unit weight (kg/m³)	COV_c,tanØ,γ
100	35	2600	0.1~0.5

해석결과를 살펴보면 전반적으로 입력한 변동계수보다 사면 안전율의 변동계수가 적게 평가되는 결과를 보였다. 또한 입력변동성 0.1~0.2구간에서는 Taylor series방법이, 0.3~0.5구간에서는 PEM방법이 MCS의 결과와 유사한 결과를 나타낸다(Table 9 참조).

Table 9.

COV of Safety factor using probabilistic methods (considering cohesion, coefficient of friction, unit weight)

COV_c,tanØ,γ	MCS	FOSM	PEM	Taylor Series
0.1	0.074908	0.070947	0.083526	0.074546
0.2	0.151401	0.141895	0.146541	0.149468
0.3	0.231429	0.212842	0.227613	0.225246
0.4	0.317639	0.283790	0.321386	0.302620
0.5	0.409031	0.354737	0.422144	0.382912

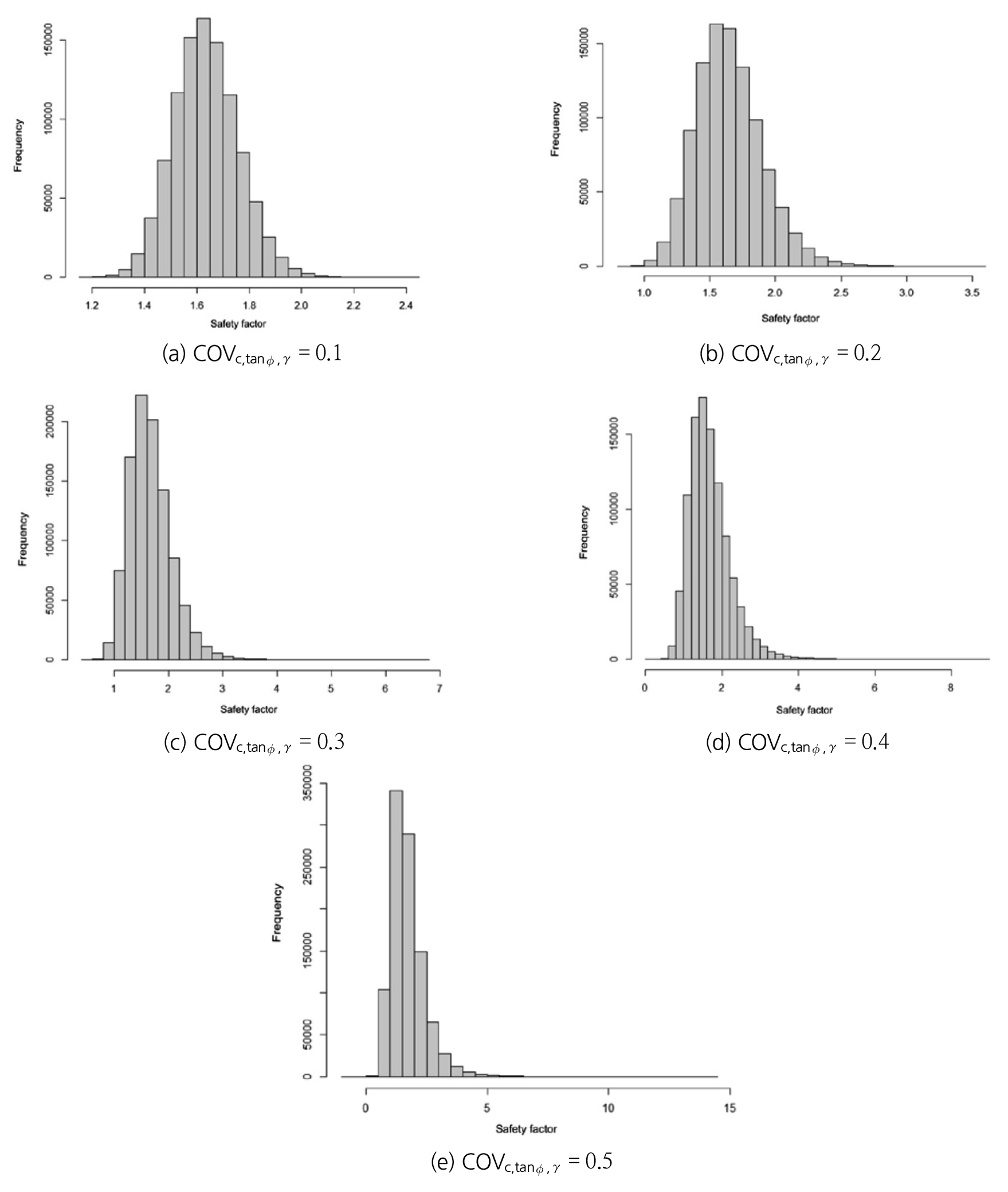
MCS를 이용하여 해석한 입력한 변동계수에 대한 사면안전율의 분포를 보면 Fig. 6과 같다. 사면안전율의 분포는 입력한 확률분포와 같은 대수정규 분포형으로 표시되었으며, 입력한 변동계수가 커질수록 최빈치(mode)가 왼쪽으로 치우치는 양의 왜곡도를 가지는 특성을 나타낸다.

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F6.jpg

Fig. 6

Distribution of safety factor using MCS

간이 확률해석법 PEM방법으로 계산한 모형2에 대한 사면 안전율분포를 정규분포로 가정한 경우와 대수정규분포로 가정한 경우에 따른 입력한 변동성에 대한 신뢰지수와 파괴확률은 Table 10과 같다. 모형1과 유사하게 입력한 변동계수가 0.2보다 큰 경우는 결정론적 안정성(F>1.5)은 만족하나, 파괴확률은 0.001보다 커서 확률론적 안정성은 만족하지 못하는 결과를 보여주었다.

Table 10.

Reliability index and failure probability for plane failure considering cohesion, coefficient of friction, unit weight

COV_c,tanØ,γ	Reliability index (β)		Failure probability (p_f)
COV_c,tanØ,γ	normal	log normal	normal	log normal
0.1	4.35E+00	5.37E+00	6.90E-06	3.96E-08
0.2	2.651427	3.301839	0.004008	0.000480
0.3	1.878803	2.370385	0.030136	0.008885
0.4	1.481920	1.906178	0.069181	0.028314
0.5	1.255632	1.662258	0.104625	0.048231

https://static.apub.kr/journalsite/sites/ksrm/2021-031-05/N0120310503/images/ksrm_31_05_03_F7.jpg

Fig. 7

Reliability index vs. COV

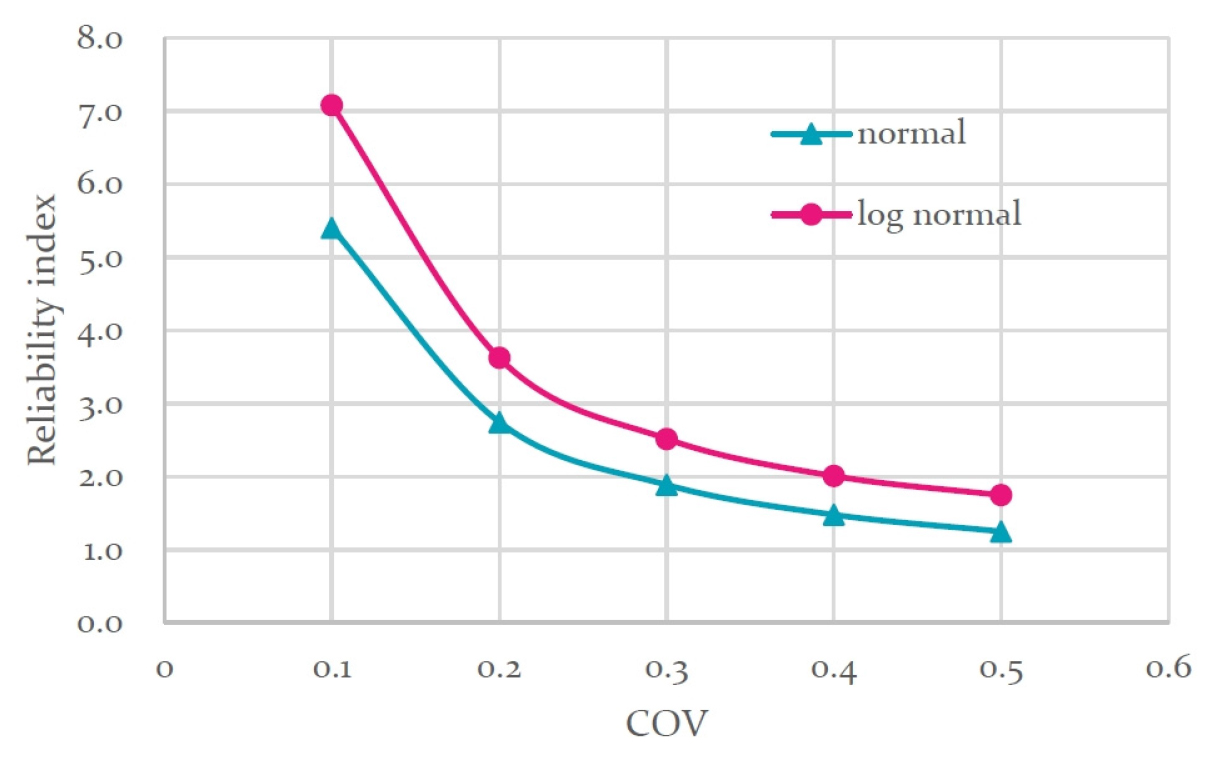
COV에 따른 사면안전율에 대한 신뢰지수를 표시한 Fig. 7의 해석결과를 살펴보면 입력변동의 크기에 따라서 사면안전율에 대한 신뢰지수가 감소하며, 대수정규분포로 가정한 경우가 정규분포로 가정한 경우보다 다소 크게 평가되는 것을 알 수 있다. 또한, 이러한 확률론적 해석은 아래와 같은 검토식에 의하여 보다 합리적인 설계를 가능하게 한다.

(25)

(중요도에 따른 파 괴 확 률) \times (파 괴시 복구비용) > (신뢰성 해 석에 대 한 추 가비용)

5. 결 론

확률변수로 점착력, 마찰계수, 단위중량을 고려한 암반사면의 평면파괴 안전율에 대하여 여러 확률론적 해석법을 적용하여 분석한 내용을 정리하면 다음과 같다.

1) 확률변수로 점착력, 마찰계수, 단위중량을 고려한 평면파괴에 대한 사면안전율의 민감도는 점착력, 마찰계수, 단위중량 순으로 큰 영향을 미친다.

2) 입력변수의 변동계수와 대비하여 사면안전율의 변동계수는 다소 적게 평가되었으며, MCS와 간이 확률해석법(FOSM, PEM, Taylor series)들의 해석결과는 안전율과 확률변수 간의 선형관계 경우가 보다 유사한 결과를 나타낸다.

3) 입력하는 확률변수의 변동의 크기에 따라서 사면안전율의 신뢰지수는 비례하여 감소하며, 사면안전율에 대한 확률분포를 대수정규분포로 가정하는 것이 정규분포로 가정한 것보다 다소 크게 평가된다. 또한, 입력한 변동계수가 0.2보다 큰 경우 결정론적 안정성은 만족하지만, 확률론적 안정성은 만족하지 못하는 경우가 발생된다.

4) 기존의 결정론적 암반사면 안정해석법에 비하여 확률론적 해석법은 확률변수의 변동성을 고려하여 사면안전에 대한 파괴확률 및 신뢰지수를 평가하므로 보다 합리적인 설계가 가능하다.

References

김승곤, 김준홍, 강진태, 이지훈, 김민섭, 김종렬, 2008, 신뢰성해석을 이용한 암반사면의 평면파괴에 관한 안정성 해석, 대한토목학회 학술대회, 2976-2979.

배규진, 박혁진, 2002, 불연속면의 확률특성을 고려한 암반사면의 평면파괴확률 산정. 한국지반공학회지, 18, 97-105.

윤우현, 천병식, 2003, 불연속면의 비선형 전단강도를 이용한 암반사면 쐐기파괴 확률 해석, 한국지반공학회논문집, 19(6), 151-160.

장연수, 오승현, 김종수, 2002, 암반사면의 평면파괴에 대한 신뢰성해석, 한국지반공학회논문집, 18(4), 119-126.

Duncan, J. M., 2000, Factors of safety and reliability in geotechnical engineering, Journal of geotechnical and geoenvironmental engineering, 126(4), 307-316. 10.1061/(ASCE)1090-0241(2000)126:4(307)

Griffiths, D. V., Fenton, G. A. and Tveten, D. E., 2002, Probabilistic geotechnical analysis: How difficult does it need to be. In Proceedings of the International Conference on Probabilistics in Geotechnics: Technical and Economic Risk Estimation, Graz, Austria, United Engineering Foundation, New York, 3-20

Hoek, E. and Bray, J. D., 1981, Rock slope engineering, Revised Third Edition, The Institution of Mining and Metallurgy, London, 183~185 10.1201/9781482267099PMC1419314

Kamien, D. J., 1997, Engineering and Design: Introduction to Probability and Reliability Methods for Use in Geotechnical Engineering, CORPS OF ENGINEERS WASHINGTON DC.

Park, H. J. and Baek, J., 2007, 최우추정량기법와 점추정법을 이용한 쐐기파괴의 파괴확률 산정. In Proceedings of the KSEEG Conference: The Korean Society of Economic and Environmental Geology, 631-633

Schweiger, H. F., Thurner, R. and Pöttler, R., 2001, Reliability analysis in geotechnics with deterministic finite elements-Theoretical concepts and practical application. International Journal of Geomechanics, 1(4), 389-413. 10.1061/(ASCE)1532-3641(2001)1:4(389)

Tunnel and Underground Space ISSN:1225-1275(Print) 2287-1748(Online) 터널과 지하공간

Preview

A Comparative Study of Simplified Probabilistic Analysis Methods for Plane Failure of Rock Slope

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Fig. 1

The probabilistic design model

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

Fig. 2

PEM sampling points

(20)

(21)

(22)

Fig. 3

Plane failure without tension crack (model 1)

(23)

Fig. 4

Plane failure with tension crack (model 2)

(24)

Table 1.

Input parameters on plane failure without tension (model 1)

Table 2.

Taylor series reliability analysis for plane failure without tension crack (model 1)

Table 3.

The result of COV on the plane failure without tension crack (model 1)

Table 4.

Average safety factor for plane failure without tension crack (model 1) using monte carlo simulation

Table 5.

COV of Safety factor using probabilistic methods (considering cohesion, coefficient of friction)

Table 6.

COV of Safety factor using probabilistic methods (considering cohesion, coefficient of friction, unit weight)

Table 7.

Reliability index and failure probability for plane failure considering cohesion, coefficient of friction, unit weight

Fig. 5

Reliability index vs. COV

Table 8.

Input parameters on plane failure (model 2)

Table 9.

COV of Safety factor using probabilistic methods (considering cohesion, coefficient of friction, unit weight)

Fig. 6

Distribution of safety factor using MCS

Table 10.

Reliability index and failure probability for plane failure considering cohesion, coefficient of friction, unit weight

Fig. 7

Reliability index vs. COV

(25)

References