1. 서 론
2. GREAT 셀을 이용한 삼축압축시험 사례
3. 인공시료 실험사례에 대한 수치모사
3.1 해석모델 및 조건
3.2 해석 결과
4. 균열이 포함된 시료에 대한 수치해석
4.1 해석모델 및 조건
4.2 해석 결과
5. 결 론
1. 서 론
Geo-Reservoir Experimental Analogue Technology (GREAT) 프로젝트는 2012년 에든버러 대학교(The University of Edinburgh), 괴팅겐 대학교(University of Göttingen), 헤리엇 와트 대학교(Heriot-Watt University)가 공동으로 연구비를 지원하여 시작된 사업이다(The University of Edinburgh, 2022a). 이 프로젝트에서 개발된 GREAT 셀은 심부지층의 물리적 조건을 실험실에서 구현하기 위해 고안되었다. 유럽연합(European Union)의 FracRisk 프로젝트에서는 GREAT 셀을 활용한 심부지층 특성평가와 관련된 연구를 수행하였다. FracRisk 프로젝트는 2015년 6월 ~ 2018년 5월에 수행된 사업으로서 유럽위원회(European Commission)의 재정지원으로 수행되었으며, 에든버러 대학교가 프로젝트 주관기관 역할을 하였다(European Commission, 2022). 이 프로젝트의 연구목적은 유럽지역에서 발견된 주요 셰일가스 저류층의 개발을 위한 수압파쇄법의 이해도를 높이고, 수압파쇄로 인한 주변 영향의 저감 및 방지기술을 개발하는 것이었다(European Commission, 2018). GREAT 셀에 대한 연구는 이 프로젝트의 세부주제 중 하나로 수행되었으며, 에든버러 대학교, 괴팅겐 대학교, 헤리엇 와트 대학교가 참여하였다(European Commission, 2018). 에든버러 대학교의 GREAT 셀 연구실의 자료에 따르면, GREAT 셀은 심도 3~4 km 지층의 열-수리-역학적 조건을 실험실에서 모델링하기 위해 설계되었다. 최대로 적용가능한 장비 제원으로는 응력 100 MPa, 온도 100°C, 유체압력 40 MPa(유체흐름 고려가능)이고, 직경 0.2 m의 시료를 대상으로 한다(The University of Edinburgh, 2022b). 시료의 길이방향 축을 중심으로 회전하는 측면의 분할된 가압장치들을 이용하여 다양한 구속압 조건을 설정할 수 있고 균열이 포함된 시료에 대해 실험이 가능하다. 시료의 변형 및 열적 반응은 시료에 부착되는 광섬유 케이블(fibre optic cable)에 의해 계측되고 압력센서들을 통해 응력과 유체압력이 측정된다. FracRisk 프로젝트에서는 당초 유럽의 셰일층을 대상으로 GREAT 셀을 이용한 실험을 수행하려고 했으나, 셀 크기에 적합한 코어형태의 시료채취가 어려워 실제 지층에 대한 연구는 수행하지 못하였고 고분자(polymer) 재질의 인공시료를 생성하여 실험을 먼저 실시한 것으로 보고되었다(European Commission, 2017).
원통형 시료에 대한 통상적인 삼축압축시험에서는 시료의 원주방향을 따라 일정하게 측면 구속압이 적용되므로 비교적 용이하게 시험과정을 수치해석적으로 모사할 수 있다. GREAT 셀은 시료의 원주방향을 따라 일정 간격으로 다중의 측면 가압장치들이 설치되고 각 가압장치에 개별적으로 구속압이 적용된다. 또한, 동일한 시료에 대해 방향성이 다른 응력장을 다중으로 구현하기 위해 시료의 길이방향 축을 중심으로 가압장치들을 다단계로 회전시키면서 실험이 실시될 수 있다. 따라서 시료의 측면에 작용하는 원주방향의 구속조건이 수치해석적으로 적절히 모델링되는지를 검증할 필요가 있다. 본 연구에서는 GREAT 셀을 이용한 삼축압축시험의 수치해석 예비연구로서 역학적 시험조건에 대한 사례연구를 통해 수치모델링의 적정성을 검토하고자 하였다. 이를 위해 균열이 없는 고분자 재질의 시료에 대한 삼축압축시험 실제 사례를 모델링하여 실험결과와 비교 분석하였다. 추가적으로 단일 균열이 포함된 가상의 시료 모델을 구성하여 균열면의 마찰 특성 및 형상이 시료의 역학적 변형에 미치는 영향을 조사하였다.
2. GREAT 셀을 이용한 삼축압축시험 사례
GREAT 셀은 직경 0.2 m, 길이 0.2 m의 원통형 시료를 대상으로 한 시험장비로서 개략적인 구성은 Fig. 1과 같다. 시료 측면의 반경방향 압력은 유체로 채워진 불소 고무(flouro-elastomer) 튜브를 통해 가해지며, Fig. 2와 같이 시료 둘레를 따라 총 16개의 고무 튜브가 설치된다. 고무 튜브는 PEE (pressure exerting element)로 명명되었고 시료 중심을 기준으로 마주보는 2개의 PEE가 한 쌍을 이루어 동일 압력이 적용된다. 각 PEE의 경계부에는 인접한 PEE들의 설정된 유체압력에 영향을 미치지 않도록 밀봉재가 설치되었다. PEE들은 회전이 가능하여 구속압 조건을 다양하게 설정할 수 있다. 시료의 변형거동은 시료 표면에 설치되는 광섬유 변형율 게이지에 의해 측정된다. McDermott et al.(2018)은 고분자 재질의 인공시료를 대상으로 GREAT 셀을 이용한 삼축압축시험을 수행하였고, OpenGeoSys (OpenGeoSys Community, 2022) 수치코드에 의해 실험과정을 모사하였다. 수치해석 모델은 Fig. 3과 같이 구성되었고 시료표면의 원주변형률(circumferential strain)을 계산하여 실험결과와 비교 분석하였다. 실험에 사용된 인공시료의 재료물성은 밀도 2,000 kg/m3, 탄성계수 3.85 GPa, 포아송비 0.4이었고 재료의 탄성 거동을 가정하였다. 역학적 조건만 고려한 실험에서 시료 측면의 가압조건은 Table 1과 같다. 총 9개의 가압조건이 PEE의 회전을 고려하여 설정되었고 동일한 시료에 대해 순서대로 측면부에 압력이 가해졌다. 앞서 언급한대로 서로 마주보는 PEE들은 Table 1의 압력과 동일한 조건으로 적용되었다. 하중조건 LS1의 경우, 각 PEE에 작용하는 압력이 완전히 동일하지는 않지만 시료 측면에 균등한 압축응력을 가하기 위한 조건으로 설정되었고, 하중조건 LS2~LS9는 수평방향의 주응력들이 서로 다른 삼축압축조건을 생성하기 위해 설정되었다. 이를 고려하여 본 연구에서 는 LS1 조건은 균등한 구속압 조건, LS2~LS9는 불균등한 구속압 조건으로 구분하여 해석결과를 설명하였다. 시료에 작용하는 수직응력은 8.2 MPa로 고정되었다.
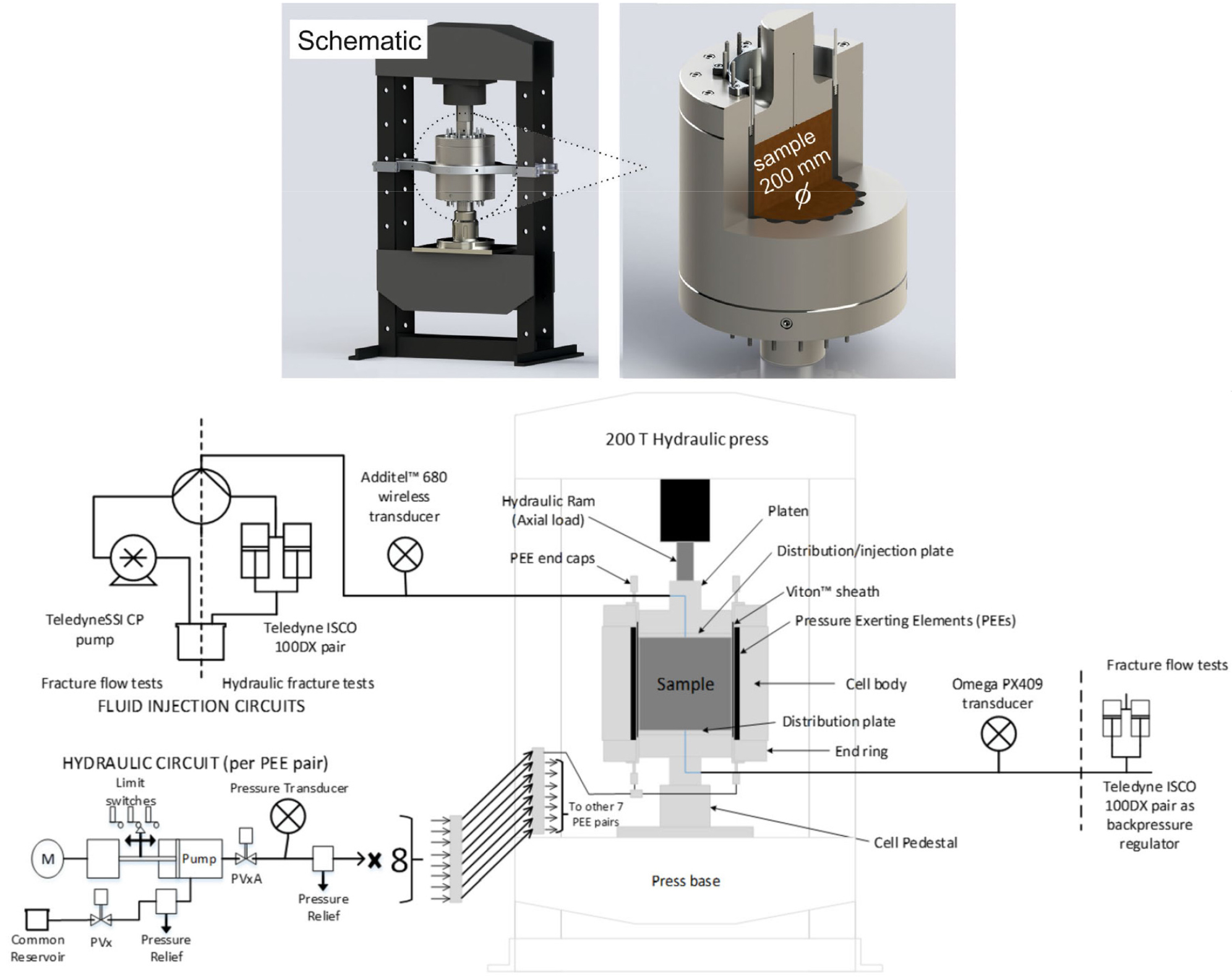
Fig. 1.
Schematic illustration of the GREAT cell set-up (McDermott et al., 2018, Fraser-Harris et al., 2020)
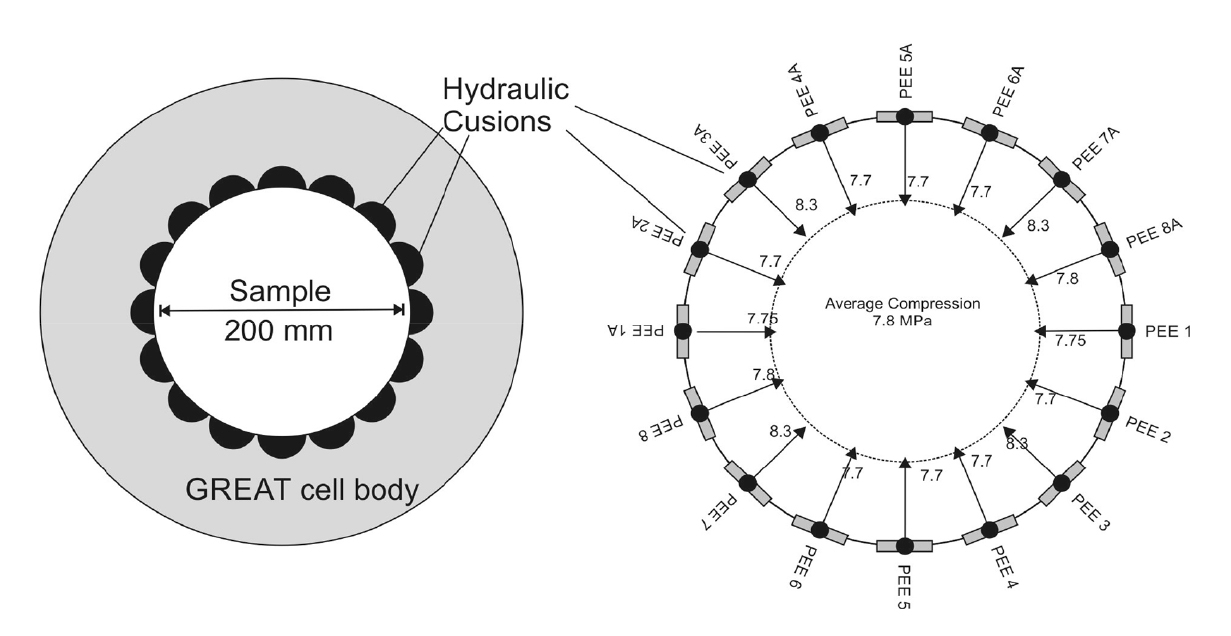
Fig. 2.
Schematic illustration of the pressure exerting elements for lateral loading (McDermott et al., 2018)
Table 1.
Lateral loading conditions applied in McDermott et al. (2018)
3. 인공시료 실험사례에 대한 수치모사
3.1 해석모델 및 조건
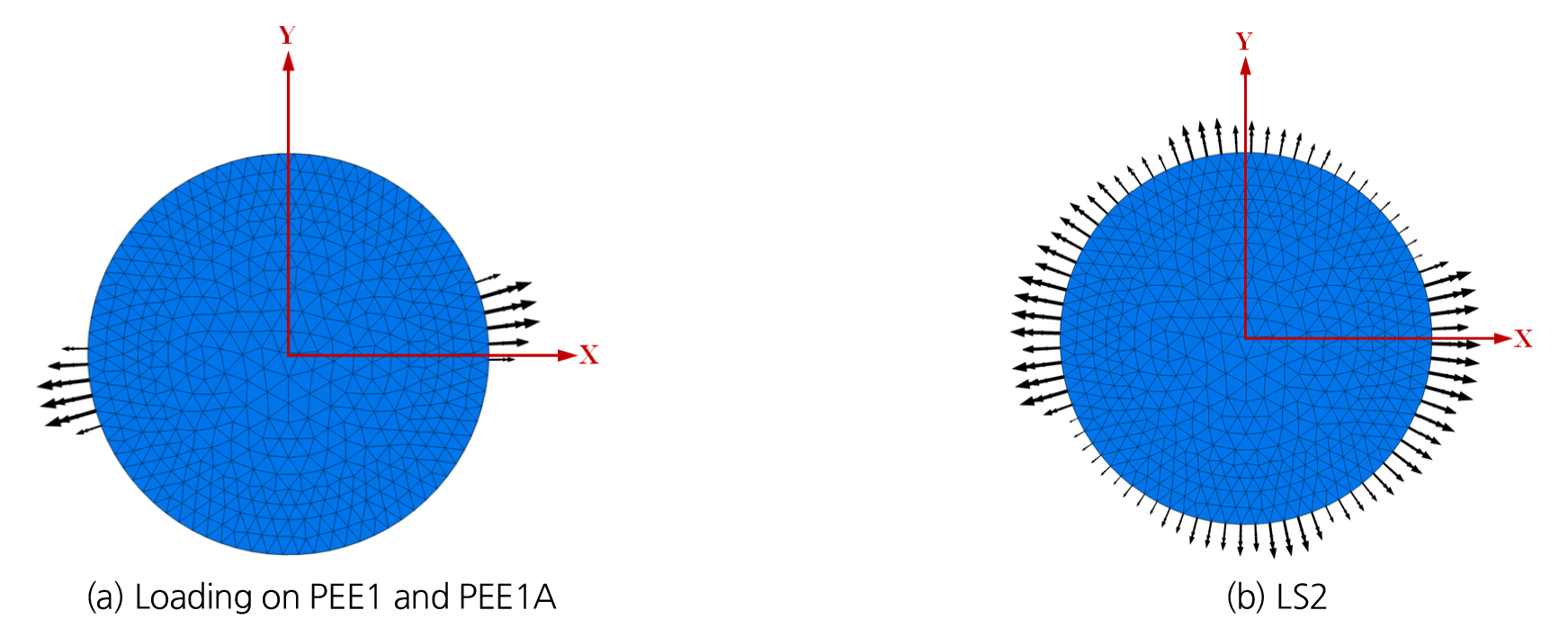
본 연구에서는 FLAC3D (Itasca, 2022)를 이용하여 2절에서 언급한 실험사례를 수치해석적으로 모사하였고 실험자료와 결과를 비교하여 모델링의 적정성을 검토하고자 하였다. 측면 가압장치인 PEE들에 작용하는 유체압력의 모델링 관련하여 PEE 경계부에 해석절점들을 위치시킨 경우(Mesh-A)와 그렇지 않은 경우(Mesh-B)를 설정하여 결과를 비교하였다. Fig. 4는 두 가지 경우의 수치해석 모델들을 나타내고, PEE 경계에 절점을 위치시킨 경우는 요소갯수 56,070개, 그렇지 않은 경우는 요소갯수 42,026개로서 PEE 경계에 절점을 위치시키기 위해 요소갯수가 다소 증가하였다. Fig. 5는 PEE 경계에 절점이 위치한 경우의 측면 구속압 적용조건을 나타낸다. Fig. 5(a)는 가압장치가 X축으로부터 반시계 방향으로 11.25° 회전된 경우에 한 쌍을 이루는 PEE1과 PEE1A에 작용하는 하중을 나타내고, Fig. 5(b)는 LS2 하중조건을 나타낸다. 측면 구속압 조건의 확인이 용이하도록 실제 하중방향과는 반대로 적용하중 벡터를 표시하였다. 실험조건과 동일하게 시료길이 방향의 중간부(높이 0.1 m)에 띠모양으로 계측지점을 설정하여 시료 표면의 둘레를 따른 원주변형률을 측정하였다. 시료는 탄성 재료모델로 설정되었고 재료물성은 밀도 2,000 kg/m3, 탄성계수 3.85 GPa, 포아송비 0.4이었다. Table 1에 표시된 하중번호를 따라 순서대로 시료 측면에 구속압을 적용하고 각 하중단계에서 원주변형률을 계산하였다.
3.2 해석 결과
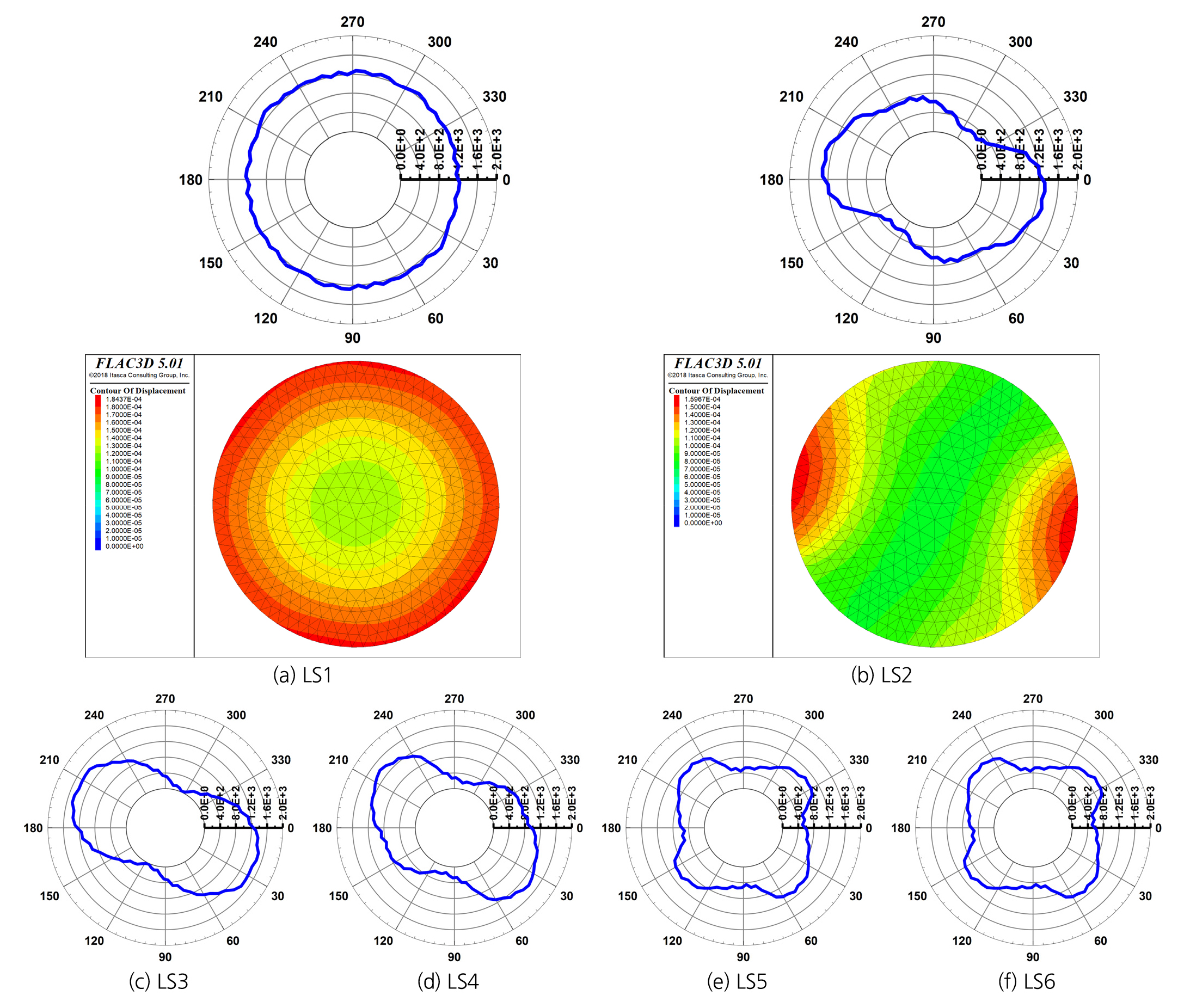
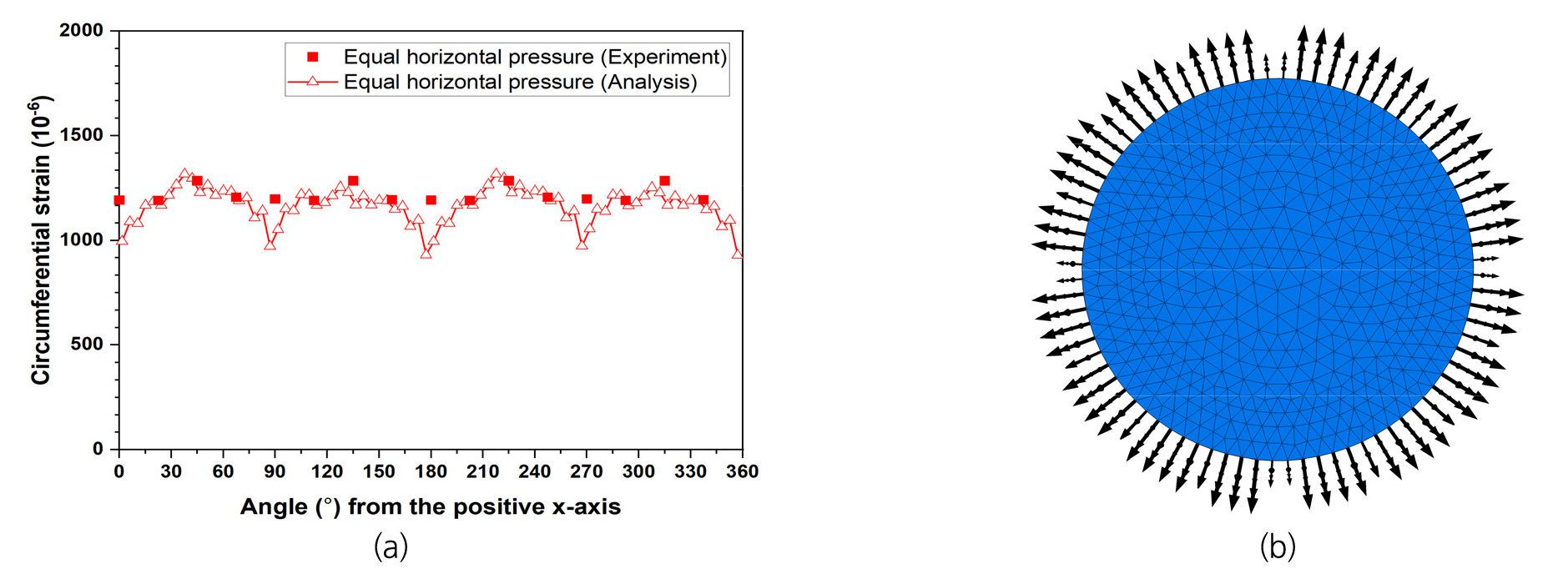
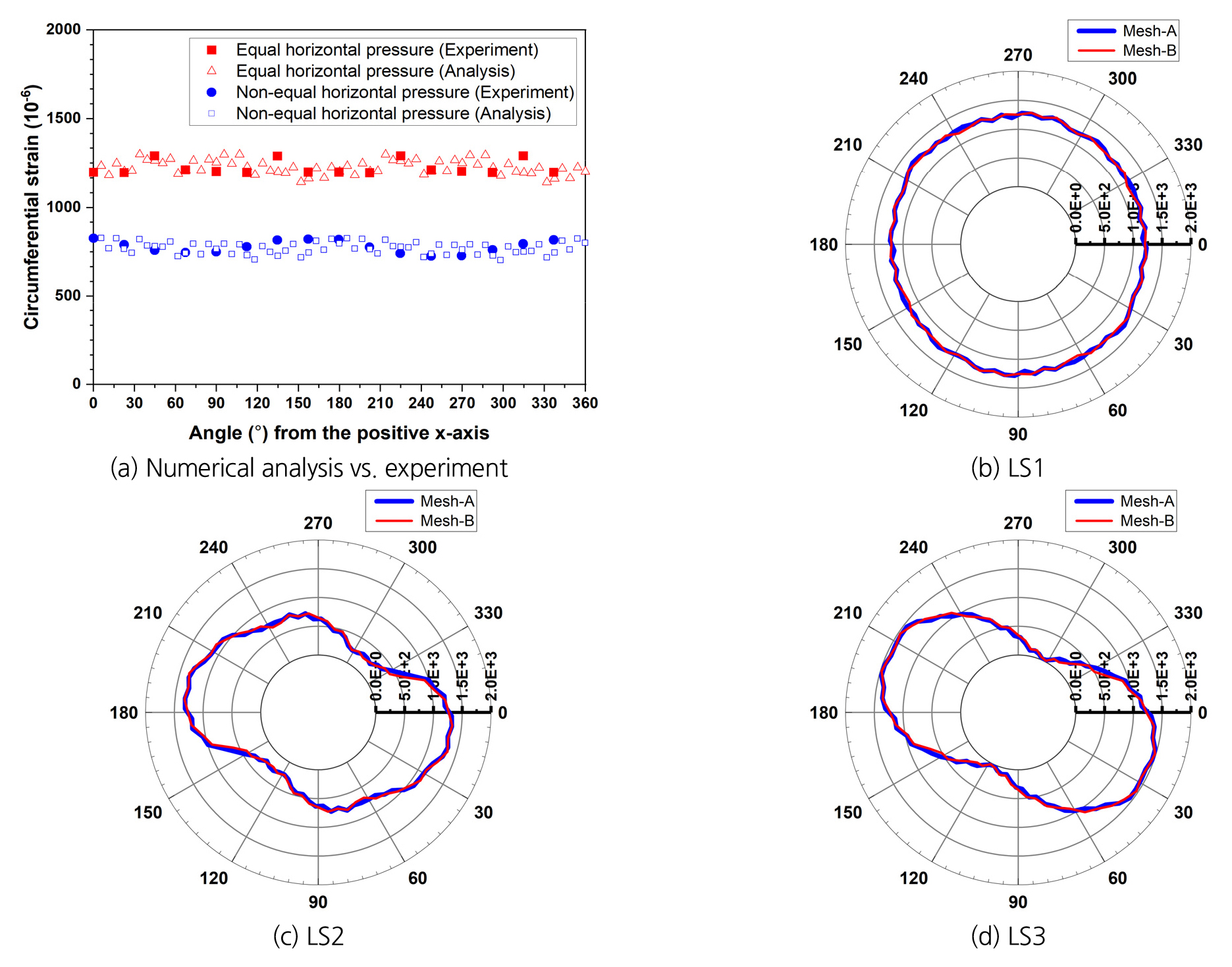
Fig. 6은 해석메쉬 Mesh-A에 대한 측면의 하중조건별 시료의 변형거동 해석결과를 나타낸다. 첫 번째 하중단계 LS1에서는 각 PEE에 작용하는 압력이 완전히 동일하지는 않지만 비교적 균등하게 작용되어 시료 표면의 원주변형률이 원형 형태로 발생하는 것으로 분석되었다. 이후 LS2~LS9 하중단계는 수평방향의 주응력들이 서로 다른 삼축압축조건을 구현하기 위해 각 PEE에 작용하는 압력에 차이를 두었고 PEE들의 회전을 고려하였다. Fig. 6(b)~(f)로부터 불균등한 구속압 조건 및 측면 가압장치의 회전에 따라 시료의 둘레를 따른 변형이 LS1 조건에 비해 점차적으로 찌그러지는 것을 알 수 있다. Fig. 6(a)와 6(b)의 등고선 그래프는 시료 길이방향의 중간부 단면에서 발생변위 분포를 나타내고 원주변형률 발생경향과 유사함을 확인할 수 있다. Fig. 7(a)는 McDermott et al.(2018)이 제시한 OpenGeoSys 수치해석 결과와 실험값을 비교하는 그래프이고, Fig. 7(b)는 본 연구의 해석결과와 실험값의 비교 자료이다. 그림으로부터 McDermott et al.(2018)의 결과와 유사하게 본 연구의 해석결과가 실험자료와 비교적 잘 일치하는 것을 알 수 있다.
GREAT 셀 측면부 가압장치의 구속압 조건이 실험조건과 다르게 적용되는 경우에 대해 시료의 변형거동을 분석하였다. LS1 하중조건에서 일부 PEE들(X축으로부터 0°, 90°, 180°, 270° 부근 등)의 경계부에 인접한 PEE의 구속압이 제대로 적용되지 않은 경우(Fig. 8(b))를 가정하여 수치해석을 수행하였고 해석결과는 Fig. 8(a)과 같다. Fig. 7(b)의 균등 구속압 조건의 결과와는 다르게 구속압이 제대로 적용되지 않은 PEE 위치(X축으로부터 0°, 90°, 180°, 270° 부근)에서 실험값과 편차가 비교적 크게 발생하는 것으로 나타났다. GREAT 셀 시험의 수치모사 시, 가압장치들의 경계가 서로 접하므로 인접한 양쪽 가압장치의 압력이 경계부에서 실제 시험조건과 동일하게 적용되는지 확인할 필요가 있을 것으로 판단된다.
Fig. 9는 해석메쉬 Mesh-B에 대한 측면의 하중조건별 시료의 변형거동 해석결과를 나타낸다. 측면 가압장치 PEE 경계부에 해석절점을 위치시킨 Mesh-A와 비교했을 때 두 가지 해석에 차이는 미미한 편으로 거의 동일한 해석결과가 계산되었다고 판단할 수 있다. 따라서 계산효율 측면에서는 PEE 경계에 해석절점을 위치시키기 위해 해석요소가 더 많이 모델링된 Mesh-A보다는 그렇지 않은 Mesh-B가 상대적으로 유리할 것으로 판단된다. 열 및 유체흐름이 고려된 복합조건의 시험에서도 이와 유사한 결과가 도출되는지 추후 연구를 통해 확인할 필요가 있을 것으로 판단된다.
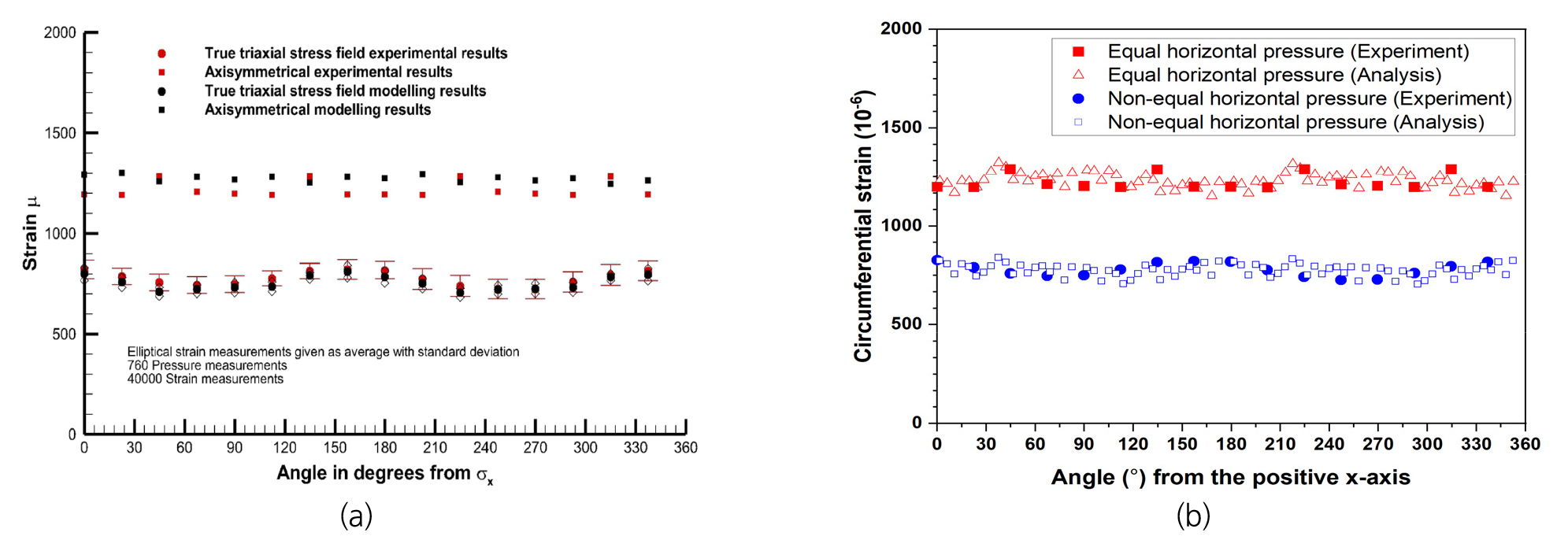
Fig. 7.
Comparison between numerical and experimental results for circumferential strain in (a) McDermott et al. (2018) and (b) the present study (Mesh-A) in which the experimental data were plotted by the screen-capture and digitization of the left figure
4. 균열이 포함된 시료에 대한 수치해석
4.1 해석모델 및 조건
균열이 포함된 시료에 대해 GREAT 셀 삼축압축시험을 수행하는 경우 시료의 변형거동을 파악하기 위해 Fig. 10과 같이 단일 균열이 포함된 가상의 시료 모델을 구성하였고, 균열면의 마찰 특성 및 형상이 역학적 변형에 미치는 영향을 분석하였다. 시료의 크기와 재료물성은 앞서 3절의 해석조건과 동일하였고, 균열 표면의 형상으로는 평평한(planar) 조건(Fig. 10(a))과 평평하지 않은 조건(Fig. 10(b))을 고려하였다. 가상의 시료에 대한 수치해석임을 감안하여 Fig. 10(b)의 균열면 굴곡은 임의로 지오메트리를 생성하여 적용되었다. 균열은 인터페이스 요소를 사용하여 모델링되었고 해석에 사용된 균열 표면의 물성은 Table 2와 같다. 표의 인터페이스 물성은 임의로 설정되었으며, 실제 시료에 대해서는 균열면의 전단시험으로부터 획득된 값을 적용할 필요가 있다. 평평한 균열 조건에서는 마찰각 10°와 30°를 모두 적용하여 수치해석을 수행하였고, 평평하지 않은 균열 조건에서는 마찰각 30°에 대해서만 해석을 수행하여 평평한 균열 조건의 변형거동과 비교하였다. 적용된 측면의 가압조건은 Table 1의 LS1~LS3이었다.
Table 2.
Parameters of fracture surface used in the present study
| Normal stiffness (Pa/m) | Shear stiffness (Pa/m) | Friction (°) | Cohesion (Pa) |
| 1.0×1010 | 0.4×1010 | 10, 30 | 0 |
4.2 해석 결과
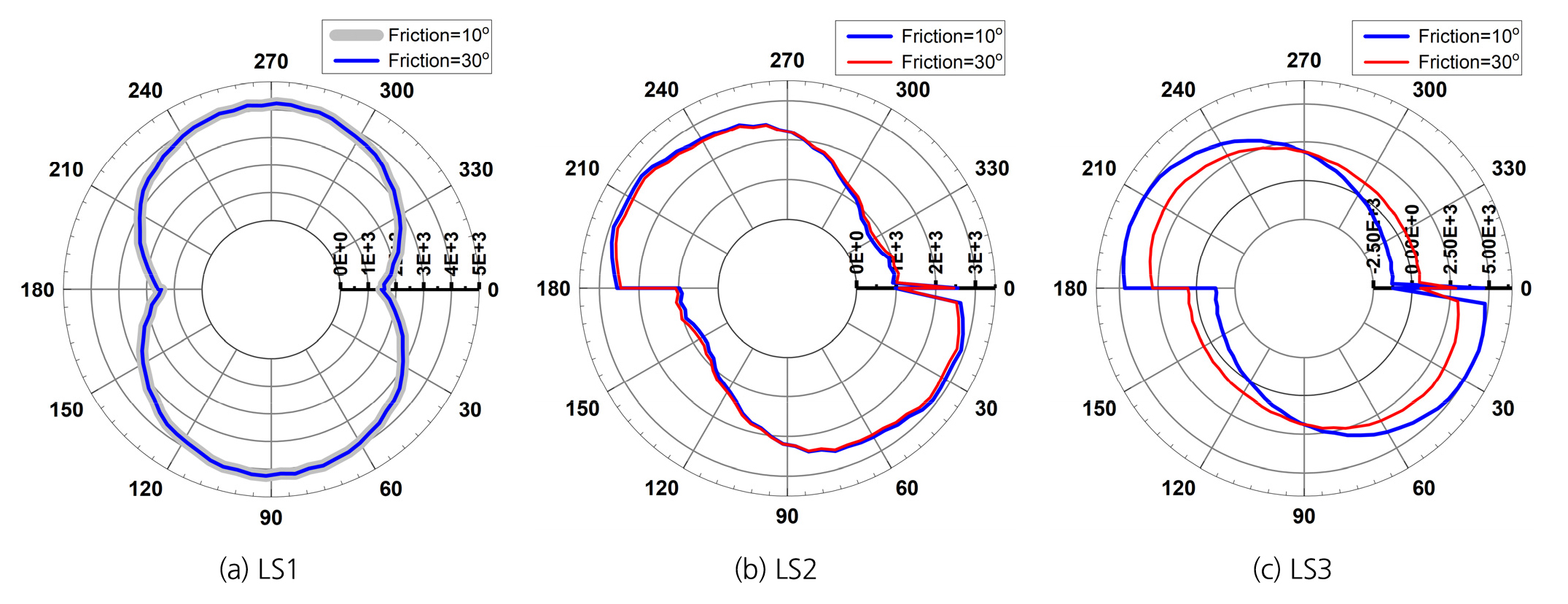
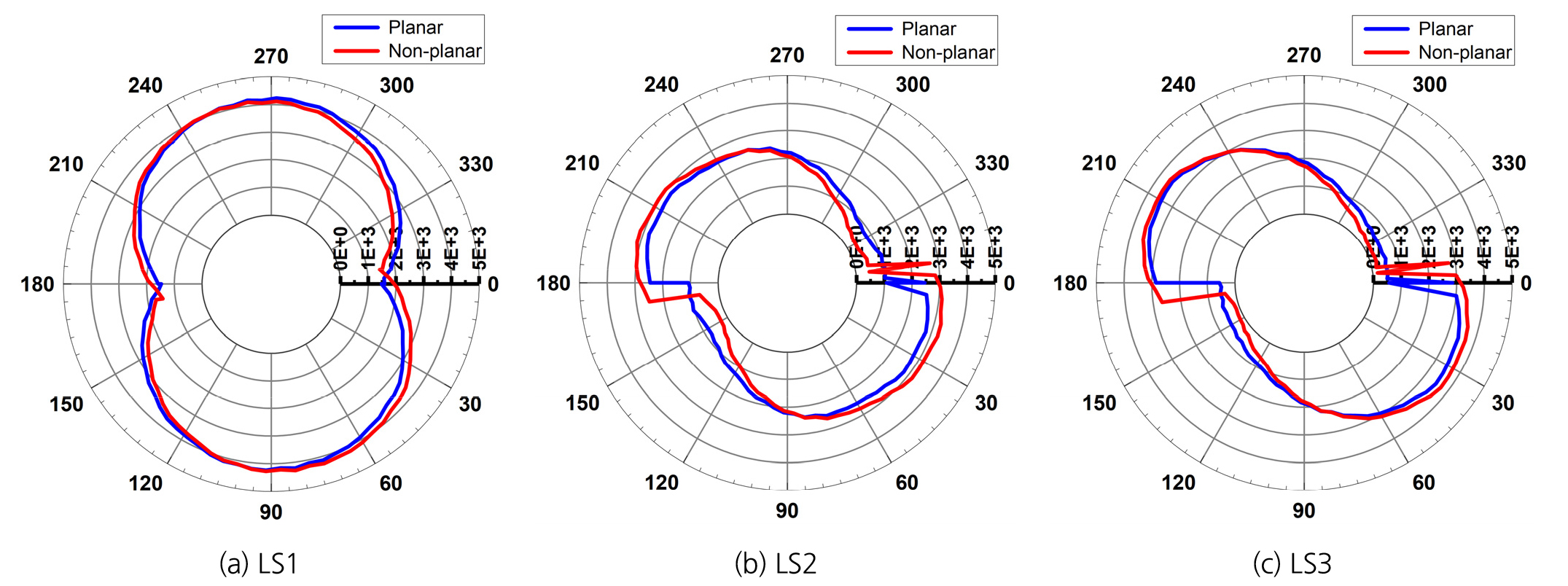
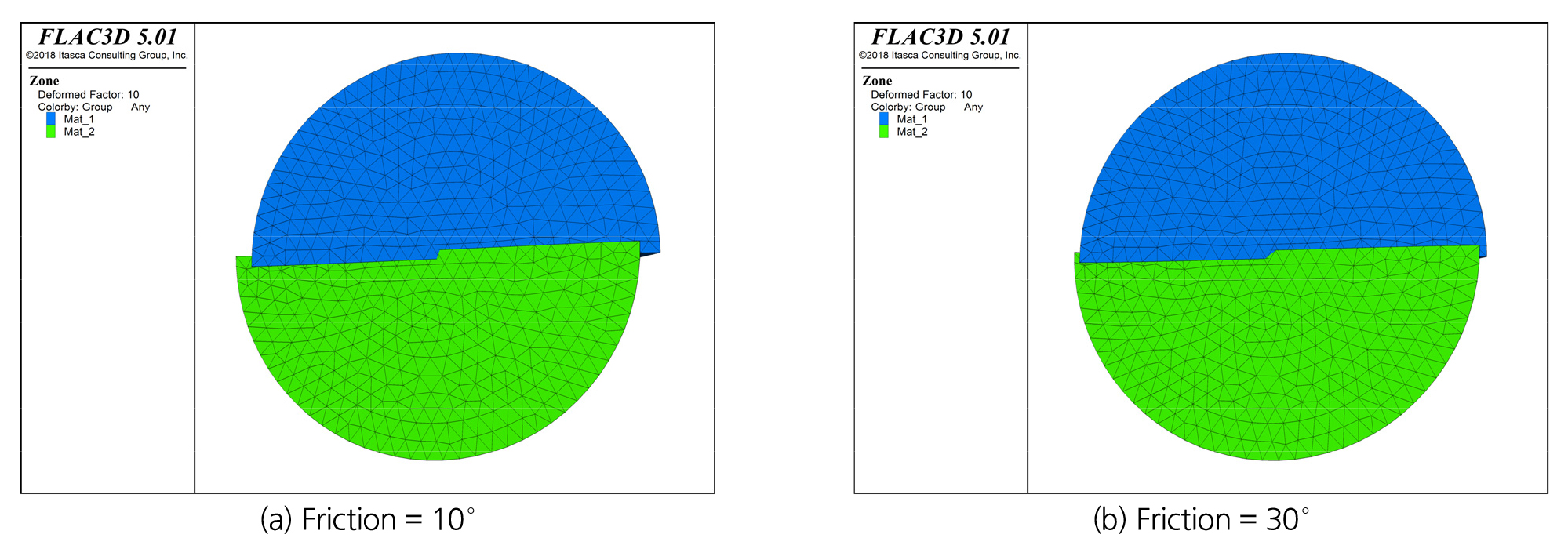
Fig. 11과 Fig. 12는 각각 평평한 균열과 평평하지 않은 균열의 해석결과를 나타낸다. 평평한 균열 조건인 경우, 균등하게 측면 구속압이 적용된 LS1 하중조건에서 균열이 없는 경우(Fig. 6(a))와 다소 다른 변형거동을 보였다. 균열이 없는 경우에는 시료 표면의 원주변형률이 원형에 가까운 형태로 발생하였으나 균열이 포함된 경우에는 Fig. 11(a)와 같이 원형이 아닌 형태로 변형이 발생하는 것으로 나타났으며, 이는 균열면의 미끌림(sliding) 및 균열 존재로 인한 강성 차이와 관련되었을 것으로 판단된다. 평평하지 않은 균열 조건에서도 유사한 변형거동 경향이 나타났다(Fig. 12(a)). 평평한 균열조건에서 균열면의 마찰 특성이 변형거동에 미치는 영향을 살펴보면, 하중조건 LS1과 LS2에서는 마찰각의 변화에 따라 시료 변형거동이 유사하지만, 하중조건 LS3에서는 원주변형률에 차이가 발생하는 것을 알 수 있다(Fig. 11). 이는 LS3 하중조건에서는 균열면의 미끌림이 마찰각 30°에 비해 마찰각 10°에서 상대적으로 더 크게 발생하여 원주변형률 분포가 다르게 나타난 것으로 판단된다. Fig. 13은 두 가지 마찰각 조건에서 해석 그리드 변형을 나타내며, 마찰각 10°인 경우 균열 부분의 변형이 더 크게 발생하는 것을 알 수 있다. 균열면의 형상이 변형거동에 미치는 영향을 살펴보면, 시료 측면의 구속압 조건별로 평평한 균열과 그렇지 않은 균열의 변형거동에 차이가 발생하였으며, 그 차이는 측면의 구속압이 균등한 경우(LS1)보다 불균등한 경우(LS2, LS3)에 상대적으로 더 크게 발생하는 것을 알 수 있다(Fig. 12). 이러한 차이는 두 가지 시료의 XY 평면상 균열의 방향성이 정확히 일치하지 않아 발생한 것도 있지만, 균열표면의 굴곡으로 인한 맞물림(interlocking) 영향이 변형거동에 포함되어 나타났을 것으로 판단된다. 향후 균열이 포함된 실제 시료에 대한 GREAT 셀 시험을 통해 균열면의 역학적 특성이 시료의 변형거동에 미치는 영향을 확인해 볼 필요가 있을 것으로 판단된다.
5. 결 론
본 연구에서는 심부지층의 물리적 환경을 구현하기 위해 개발된 GREAT 셀을 이용한 삼축압축시험을 수치해석적으로 모사하였고, 실제 실험사례 및 가상시료에 대한 해석으로부터 얻은 주요결과는 다음과 같다.
균열이 없는 인공재질의 시료에 대한 삼축압축시험 사례를 수치모사한 결과, 균등한 측면 구속압 조건과 불균등한 구속압 조건에서 시료의 변위발생 경향이 다르게 나타났으며, 해석요소 배치가 서로 다른 메쉬조건 모두에서 실험 계측값과 유사한 결과를 제공하는 것으로 검토되어 수치모델링의 적정성을 확인할 수 있었다. GREAT 셀의 측면 가압장치는 통상적인 삼축압축시험 장비와 달리 시료의 둘레를 따라 일정 간격으로 구분되어 개별적으로 구속압이 작용하므로 가압장치들 간 경계부에서 측압을 모델링하는 데 주의가 필요한 것으로 검토되었다. 가상의 균열이 포함된 시료에 대해 GREAT 셀 삼축압축시험을 수행한 결과, 균열면의 마찰 특성 및 형상이 시료의 변형거동에 영향을 미치는 것으로 분석되었다. 균열이 포함된 시료에 대해 시험과정을 모델링하는 경우, 균열의 모델링 기법 및 물성 매개변수의 신뢰도가 확보되어야 할 것이다. 연속체 해석에 의해 거친 균열을 모사하는 경우, 모델링 단순화 및 편의를 위해 균열면 형상을 평평한 것으로 가정할 수 있는데 이 방법보다는 균열면의 요철(거칠기)을 고려한 해석메쉬를 적용하여 수치모사의 정교함을 높일 필요가 있을 것으로 판단된다.
향후 GREAT 셀을 이용한 열-수리-역학적 복합조건에서의 실험자료를 벤치마크 검증할 필요가 있으며, 본 연구의 역학적 분석내용은 재료에 작용하는 열적 및 수리적 조건이 역학적 거동에 미치는 영향을 파악하기 위한 비교자료로 활용이 가능할 것으로 판단된다.