1. 서 론

고준위 방사성 폐기물을 인간 생활권으로부터 영구적으로 안전하게 격리하기 위해 현재까지 다양한 처분 개념이 제시되었으며, 그중 공학적방벽(engineered barrier system, EBS)과 자연방벽(natural barrier system, NBS)으로 구성된 다중방벽(multi-barrier system)을 이용한 심층처분개념이 경제성과 안전성 측면에서 가장 타당한 방법으로 고려되고 있다(IAEA, 2011). 스웨덴의 SKB(Swedish Nuclear Fuel and Waste Management Company)가 제안한 심층처분시스템이 대표적 사례이며, 처분용기, 완충재 등의 공학적 방벽과 심부 암반인 자연방벽으로 구성된 처분개념을 채택하고 있다. 국내의 경우 한국원자력연구원이 스웨덴 처분개념을 토대로 한국형 기준 처분시스템(Korean Reference HLW Disposal System, KRS)을 개발한 바 있다(Lee et al., 2007).

심부 지층은 천부 지층과 비교할 때, 고온, 고응력, 고압 조건의 극한 환경과 제한된 접근성으로 인해 거동 평가와 예측이 매우 어려울 뿐만 아니라, 처분장 설계가 10만년 이상의 장기거동을 대상으로 한다는 점에서 신뢰성 높은 수치해석모델의 개발은 핵심 연구테마 중 하나이다. 특히, 균열이나 절리, 단층과 같은 미시적, 거시적 규모의 불연속면들은 암반의 열, 수리적, 역학적 거동에 지대한 영향을 미치고 시설물의 불안정성을 초래하므로 이에 대한 적절한 이해와 평가는 매우 중요하다. 방사성 폐기물 처분장의 운영에 따라 발생하는 열응력과 압력의 발생은 암반 현지응력의 변화를 초래하게 되며, Lee et al.(2020)의 연구에 따르면 설계기준 온도가 100도일 때 1000년 후 주변 암반에 10~20 MPa의 유효응력 변화가 발생할 것으로 예측된 바 있다. 현지 암반의 응력 및 변위 조건을 고려할 때, 열팽창으로 인한 수직방향과 수평방향의 열응력 증가는 상이할 것으로 판단되며, 이는 경우에 따라 균열의 미끄러짐에 용이한 방향으로 응력이 재분포될 수 있음을 의미한다. 또한, 암반 내 많은 단층이 임계응력 상태에 놓여 있다는 점(Zoback and Gorelick, 2012)은 작은 압력 변화나 열응력 변화에 의해서도 단층이 재활성될 수 있음을 시사한다. 따라서 처분장의 장기 운영으로 인한 근거리 또는 원거리 불연속면의 안정성을 적절히 평가하는 것은 부지조사, 처분장 설계 및 시공 단계에서 반드시 고려해야 할 기술 요소이다.

본 연구에서는 입자기반 개별요소모델(grain-based distinct element model, GBDEM)을 이용하여 열에 의해 발생하는 암석 균열의 미끄러짐을 해석할 수 있는 해석기법을 제시하였다. 이는 DECOVALEX-2023 국제공동연구 Task G에 참여하여 수행한 연구로, 여기에서는 열-역학적 벤치마크(thermo-mechanics benchmark) 해석 결과를 소개하였다. Park et al.(2020)과 Park et al.(2021)은 사면체 블록모델과 위 해석기법을 이용해 Task G의 역학적 벤치마크 모델링과 수리-역학 벤치마크 모델링에 대한 연구 결과를 발표한 바 있다. 본 연구에서는 위 선행연구들과 달리, Voronoi 다면체 블록을 사용하여 시료 내에 유한한 길이의 암석 균열을 생성할 수 있는 모델링 기법을 제안하였다. 경계응력 및 가열로 인해 암석과 균열에 발생하는 응력변화와 변위를 정량적으로 분석하였으며, 균열 미끄러짐과 관련된 경계조건의 영향과 열-역학적 메커니즘을 고찰하였다.

2. 해석 개요

2.1 DECOVALEX-2023 TASK G

DECOVALEX 프로젝트는 1992년부터 시작된 국제공동연구로, 고준위방사성폐기물처분장의 열-수리-역학-화학적 복합거동 평가를 위한 수치해석모델의 개발을 목표로 다양한 연구가 이루어져 왔다(Birkholzer et al., 2019). 현재, 2020년부터 2023년까지 7가지 연구주제를 대상으로 하는 DECOVALEX-2023이 진행 중에 있으며, 국내에서도 한국원자력연구원과 한국지질자원연구원이 참여하여 활발한 연구를 수행하고 있다(Kim et al., 2021).

본 연구는 DECOVALEX-2023의 Task G에 참여하여 수행된 연구로서, Task G의 연구목표는 결정질 암석 내 균열의 열-수리-역학적 복합거동을 해석할 수 있는 수치해석기법을 개발하고 검증하는 것이다. 독일 Freiberg University of Mining and Technology(TUBAF)/ Helmholtz Centre for Environmental Research(UFZ), 스코틀랜드 Edinburgh 대학교, 독일 DyanFrax 사에서 공동 제안하였으며, 총 9개의 연구팀이 참여하고 있다. Task G에 대한 보다 상세한 내용은 Park et al.(2020)에 소개되어 있다.

2.2 열-역학적 벤치마크 모델

열-역학적 벤치마크 해석의 주요 연구내용은 열-역학적 커플링에 의한 암석 균열의 미끄러짐을 모사하는 것이다. Task G에서는 2차원 모델과 3차원 모델에 대한 연구가 계획되어 있으며, 여기에서는 2차원 모델에 대한 해석 결과를 소개하였다. 해석 도메인은 크기가 0.5 m×0.5 m인 결정질 암석으로 시험편 중심에 0.17 m의 유한한 길이를 갖는 단일 균열을 내포하고 있다. 균열은 편평한 면(planar fracture)으로서 수평면으로부터 60°의 경사각을 갖는다. 암석은 탄성 재료로 가정하여 균열의 성장이나 시편의 파괴가 고려하지 않으며, 균열은 인장강도를 갖는 Coulomb slip model을 따르는 것으로 간주한다.

열-역학 벤치마크 해석의 모델링 단계는 크게 두 가지로 구성된다. 먼저 수평방향으로 5 MPa(Sxx), 수직방향으로 15 MPa(Syy)의 경계응력을 적용하여 역학적 평형해석을 실시한 이후, 암석 내부의 응력이 경계응력에 충분히 도달하면 상부와 하부 경계면에 온도 50°C의 가열판을 설치하여 열전도해석 및 열-역학적 커플링해석을 수행한다. 해석모델의 초기온도는 11°C이며, 가열 중에는 모든 경계면에서 법선방향으로의 변위가 구속된 것으로 가정한다. 각 해석팀은 경계응력과 열응력을 가하면서 암석과 균열면의 응력 변화에 따른 균열의 미끄러짐 거동을 살펴보고, 해석 결과를 상호･비교함으로써 해석모델을 수정, 개선하게 된다. Table 1은 열-역학적 벤치마크 모델의 해석조건과 입력 물성을 정리한 표이다.

2.3 입자기반 개별요소모델

본 연구에서는 벤치마크 해석을 위하여 Voronoi 다면체 모델과 3DEC(Itasca CGI, 2021) 프로그램을 활용한 입자기반 개별요소모델(grain-based distinct element model, GBDEM)을 사용하였다. GBDEM은 비교적 최근에 제안된 해석 모델로 암석의 미시구조(micro-structure)를 다각형이나 다면체, 랜덤 Voronoi 모델 등을 이용해 모사한 뒤, 그 역학적 거동을 개별요소법을 통해 계산하는 방법이다. 지난 십여 년간 많은 연구를 통하여 GBDEM이 미시적 관점에서 암석의 점진적 파괴를 직접적으로 모방함으로써 암석의 취성파괴 메커니즘, 불균질성, 이방성 등을 효과적으로 반영할 수 있음이 보고되었다(Lan et al., 2010, Ghazvinian et al., 2014, Park et al., 2017, Fu et al., 2020, Wang et al., 2021, Park et al., 2021). 그러나 원이나 구를 사용하는 입자모델과는 달리, 입자간 접촉(contact) 개수가 많고 형태가 다양하여, 계산성능의 제약으로 인해 대부분 실험실 스케일의 연구에 머물러 있는 실정이다. 또한, 현재까지 수리-역학 커플링이나 열-역학 커플링이 적용된 연구사례는 거의 보고되지 않아 열-수리-역학적 거동해석 기법 개발 등 향후 지속적인 연구가 필요한 분야라고 할 수 있다.

3DEC은 개별요소법에 기초한 암반거동해석 프로그램으로 불연속 암반체를 블록(block)과 불연속면(joint)의 조합(blocky system)으로 표현한다. 블록은 강체블록(rigid block) 또는 변형가능블록(deformable block)으로 모델링할 수 있으며, 변형가능블록을 사용하는 경우 각 블록은 여러 사면체 zone 요소로 재분할된다. 블록과 불연속면에서는 구성모델과 입력물성을 통해 역학적 거동이 정의될 수 있으며, 불연속면에서의 계산은 불연속면 상의 여러 접촉(contact) 요소를 통해 이루어진다. GBDEM은 위와 같은 블록시스템을 보다 미시적 스케일의 암석에 적용하는 접근법이라고 할 수 있다. 즉, 암석 재료 자체를 작은 개별블록의 집합체로 간주하고 접촉력의 전달과 접촉의 파괴를 통해 재료의 변형과 점진적 파괴를 해석하는 기법이다.

본 연구에서는 균열을 포함한 암석 재료의 거동을 모사하기 위하여 탄성적으로 거동하는 블록들을 이용하였으며, 균열의 거동은 Coulomb slip 모델을 따르는 것을 가정하였다. 균열면 상의 contact는 전단파괴나 인장파괴 이전에는 강성(수직강성, 전단강성)에 의해 탄성적으로 거동하지만, 전단파괴 이후에는 미끄러짐(slip)이 발생하고 전단응력은 파괴 시의 값으로 재설정된다. 인장파괴가 발생한 경우에는 인장강도는 0이 되며, 점착력에 의해 전단력에 저항한다.

3DEC 내에서 열-역학 커플링은 기본적으로 일방향(one-way) 커플링을 가정한다. 즉, 가열로 인한 열응력의 증가는 모사가 가능하지만, 역학적 변화가 열유동 특성에 미치는 영향은 없는 것으로 간주한다. 열응력의 증가는 온도 증가에 의한 열팽창(열에 의한 변형)에 기인하며, 이를 관계식으로 표현하면 식 (1), 식 (2)와 같이 표현된다.

여기서 εij는 열로 인한 변형률, αt는 단위가 [1/°C]인 선형열팽창계수, δij는 Kronecker delta이다.

여기서 σij는 열로 인한 응력이며, K는 체적탄성계수로서 응력의 단위를 갖는다.

본 연구에서 고려한 Voronoi diagram은 공간을 분할하는 수학적 모델로 공간상의 임의 위치에 시드(random seed)를 분포시키고 각 시드에 대응하는 다면체를 구성하는 알고리즘이다. 공간상에서 인접한 두 시드의 연결선에 대한 수직이등분면들을 폐합하면 각 시드에 일대일 대응하는 다면체 셀(cell)을 구성할 수 있으며, 다면체의 내부는 여러 시드 중 해당 시드와 가장 가까운 점들의 집합이 된다는 특징이 있다.

3DEC은 최신 버전인 7.0부터 Voronoi 블록을 생성하는 알고리즘을 제공하고 있다. 그러나 3DEC은 기본적으로 암반 스케일의 블록을 모사하는 데에 최적화되어 있어, 본 연구와 같이 다수의 작은 블록에 대한 meshing을 진행하는 경우 블록 데이터 구조(block data structure) 생성에 오류가 발생하였다. 또한, 데이터 구조가 성공적으로 만들어진 경우에도 블록의 edge 길이를 반복적인 시행착오를 통해 설정해야 하는 등 불안정한 성능을 보였다. 따라서 본 연구에서는 Voronoi 블록 생성과 zone 요소의 그리드 작성을 위하여 별도의 프로그램인 Neper(Quey et al., 2011)와 Gmsh(Geuzaine and Remacle, 2009)를 활용하였다. Neper는 오픈소스 코드로 이를 이용하면 convex 도메인(사각형, 원, 육면체, 원기둥 등) 내에 Voronoi diagram을 생성할 수 있으며, 본 연구와 유사한 접근법을 사용한 Ghazvinian et al.(2014)의 연구에서도 이를 이용해 3DEC에서 Voronoi 블록을 생성한 바 있다. 한편, Gmsh는 3차원 유한요소 해석을 위한 그리드 작성을 목적으로 개발된 오픈소스 코드로서 현재 다양한 분야에서 복잡한 수치모델의 mesh 작성에 활용되고 있다.

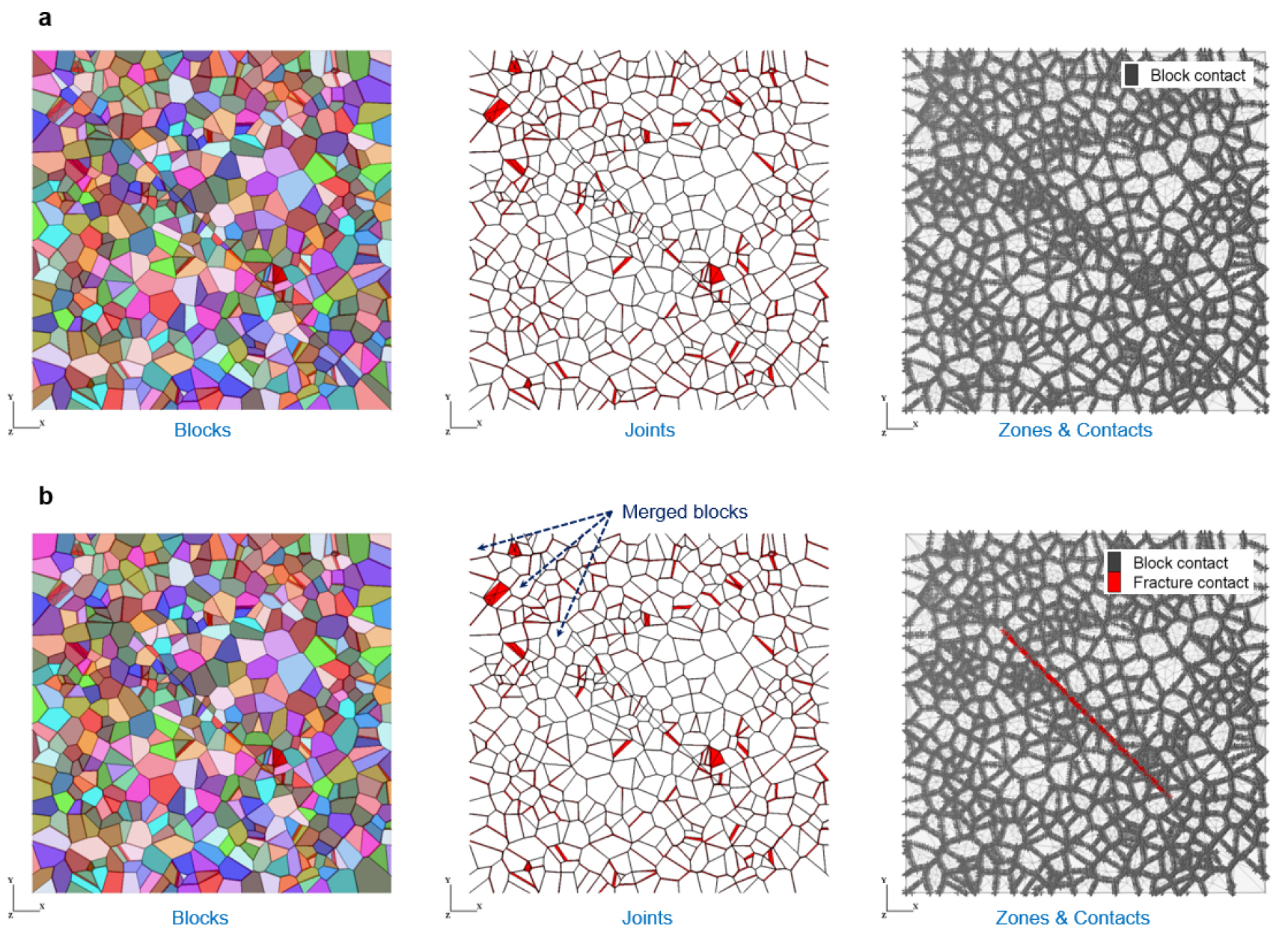
본 연구의 해석모델은 시료 내에 유한한 길이의 균열을 내포하므로, Neper만을 이용하여 블록 모델을 생성할 수 없었다. 따라서 Voronoi 블록에 균열 요소를 삽입하는 추가적인 데이터 처리가 요구되었다. Fig. 1은 3DEC에서 유한한 길이의 균열을 포함한 Voronoi 블록과 사면체 zone 요소를 생성한 예시(균열 경사 45°, 얇은 두께의 3차원 육면체 모델)를 보여주는 그림으로 모델 작성을 위한 일련의 과정을 기술하면 다음과 같다.

① Neper를 이용하여 육면체 내 Voronoi diagram을 생성하고, 유한 균열을 도메인 경계까지 연장하여 육면체를 둘로 분할한다.

② Voronoi diagram(3DEC block 요소에 상응)의 point, edge, face, volume 등의 정보를 변환하여 Gmsh의 geometry를 생성한다.

③ Gmsh에서 geometry에 해당하는 Volume 요소(다면체)를 대상으로 사면체(3DEC의 zone 요소에 상응)로 구성된 3차원 mesh를 생성한다.

④ Gmsh에서 생성된 mesh 정보(block, zone 정보)를 변환하여 3DEC에서 변형가능 블록(deformable block)을 생성하고, 블록 간 경계에 접촉(contact)을 설치한다.

⑤ 3DEC에서 암석 균열 좌표에 해당하는 불연속면과 contact를 탐색하여 균열 물성을 부여하고, ①번 과정에서 불필요하게 분할된 블록들을 탐색하여 하나의 블록으로 다시 통합한다.

Fig. 1(a)는 ① ~ ④번 과정을 통해 작성된 3DEC 모델의 블록(block), 불연속면(joint), zone, contact 요소를 보여주며, Fig. 1(b)는 ⑤번 과정을 통해 최종적으로 생성된 3DEC 모델의 블록, 불연속면, zone, contact 요소를 보여준다. Fig. 1(a)와 Fig. 1(b)의 비교를 통해, Voronoi 모델 내에 유한한 길이의 균열이 삽입되어 3DEC의 블록, zone, contact 요소들이 적절히 구성된 것을 확인할 수 있다.

Fig. 1.

Creation of a single fracture embedded in Voronoi diagram using Neper, Gmsh and 3DEC by (a) splitting domain into two halves and (b) merging partial blocks

본 연구에서는 3차원 프로그램인 3DEC을 사용하였으므로, 2차원 문제를 모사하기 위해 평면외(out-of-plane) 방향으로 평면변형률 조건을 설정하였다. 즉, 0.5 m × 0.5 m × 0.005 m 크기의 얇은 육면체 형태의 해석도메인을 작성하되, 해석 시 두께 방향의 변형을 구속하여 2차원 해석조건을 구현하였다. Fig. 2는 해석모델의 형상을 보여주는 것으로 사용된 블록의 개수는 총 6,124개이며, 부피를 기준으로 환산한 등가직경(equivalent spherical diameter, de)은 약 7.3 mm이다. Zone 요소의 개수는 총 158,333개이며 등가직경은 약 2.5 mm이다.

입자기반 개별요소모델의 입력물성을 선택하기 위해서는 보통 미시물성 조정(micro-parameter calibration)이 필요하나, 본 연구에서는 선행연구(Park et al., 2021)를 통해 제안된 등가연속체 접근법(equivalent continuum approach)을 적용하여 zone 요소와 contact 요소의 미시물성을 결정하였다. 이 방법은 입자모델을 등가연속체로 간주하고, 전체모델의 탄성거동에 대한 블록과 접촉의 기여도를 조정함으로써 미시물성을 결정할 수 있는 방법이다. 이와 관련된 자세한 내용은 Park et al.(2021)에 기술되어 있다. 여기에서는 블록과 접촉의 기여도를 각각 99%, 1%로 가정하여 미시물성을 결정하였다. 이와 같이 전체 시료의 변형에 미치는 접촉의 영향을 최소화하면, 입자의 크기효과를 감소시킬 수 있어 계산 효율을 크게 증가시킬 수 있다. 계산된 미시물성을 적용한 해석모델(Fig. 2)에 수치적인 일축압축강도시험을 수행한 결과, 해석모델의 탄성계수와 포아송비는 각각 49.6 GPa, 0.26으로 나타났으며, 이는 Table 1의 입력물성과 거의 동일한 값이다.

Fig. 2.

Model generation for thermo-mechanics benchmark

3. 해석 결과

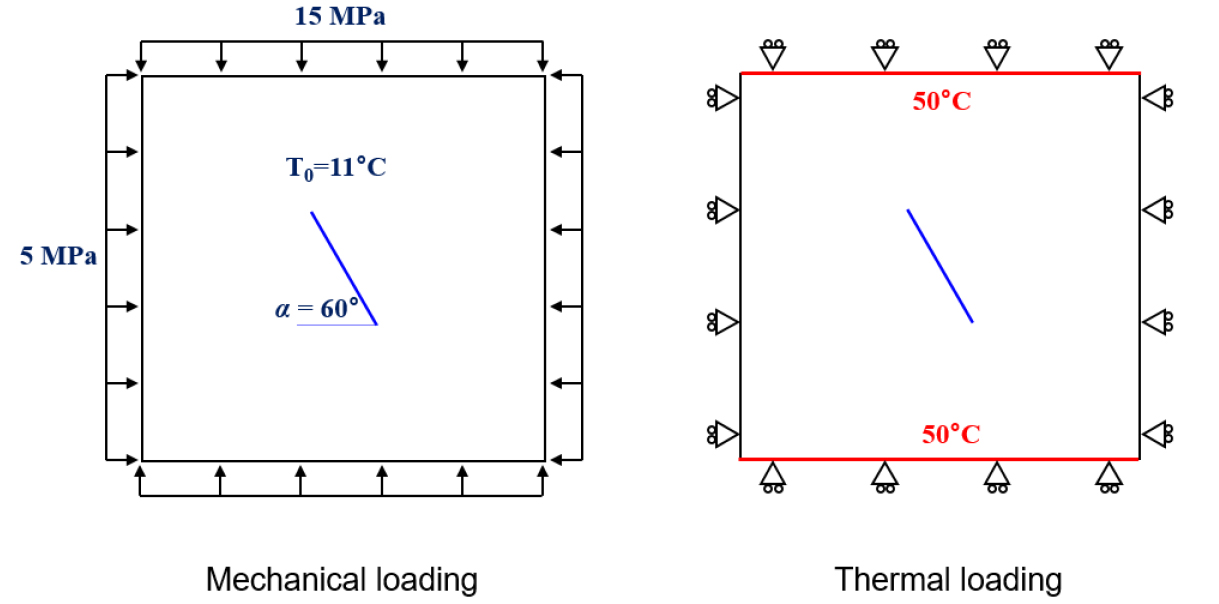
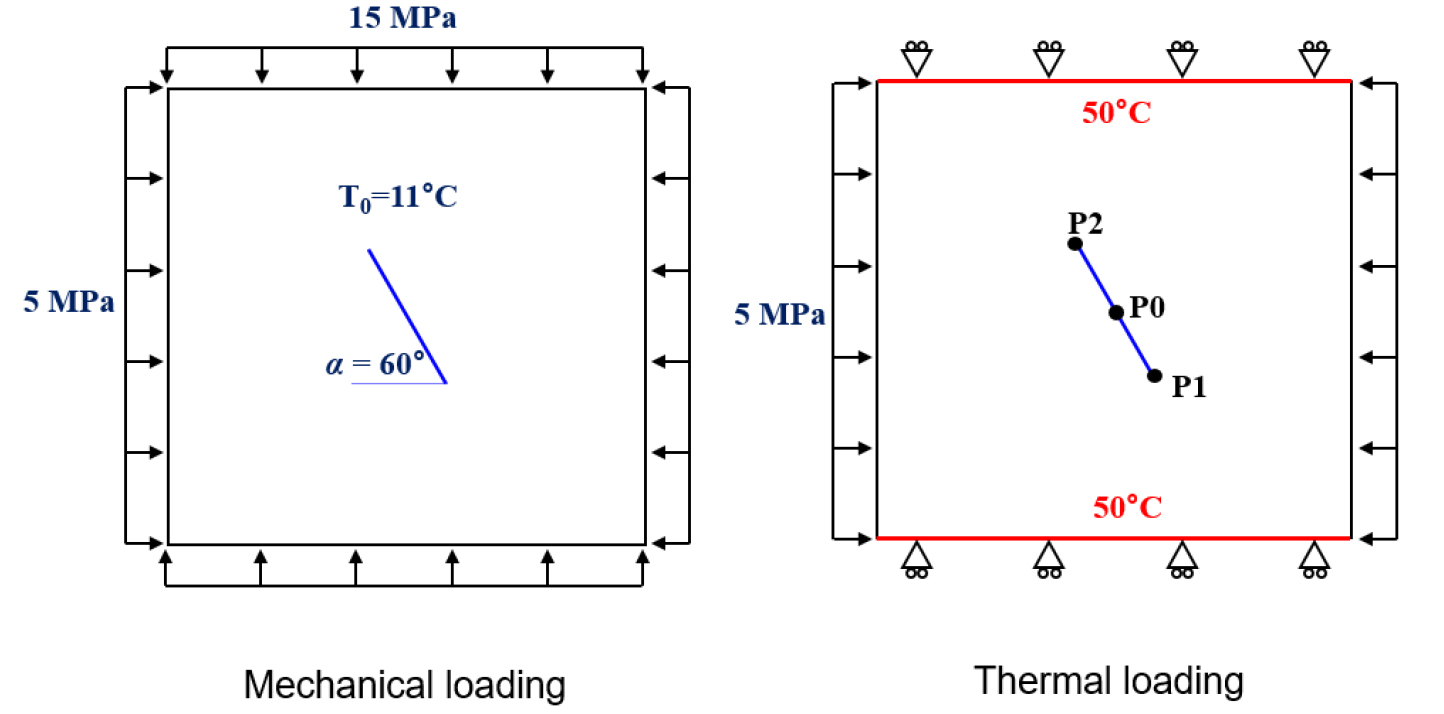
열-역학적 벤치마크 모델에서는 초기온도가 11°C인 암석시료에 일정한 경계응력을 가한 뒤 평형상태에 도달하면(1단계: 역학적 하중 재하), 전 경계의 변위를 구속하고 상하부에서 50°C의 가열판을 통해 시료를 가열하면서(2단계: 열적 하중 재하) 이에 따른 균열의 미끄러짐을 모니터링하게 된다. 이를 수치적으로 모사하기 위해서 1단계에서는 역학적 평형해석을, 2단계에서는 과도 열전도(transient heat conduction) 해석을 수행하였으며 2단계에서는 열-역학적 커플링을 통해 암석 블록의 열팽창과 열응력 증가를 고려하였다. Fig. 3은 열-역학적 벤치마크 해석을 위해 주어진 경계조건을 보여준다.

Fig. 3.

Boundary condition of thermo-mechanics benchmark model

3.1 경계응력으로 인한 균열의 역학적 거동

벤치마크 모델의 역학적 하중 재하 단계에서는 수평응력(Sxx)과 수직응력(Syy)이 각각 5 MPa, 15 MPa일 때 경계응력으로 인한 암석 균열의 거동을 살펴보았다. 시료의 초기응력은 0이며, 초기온도는 11°C이다. 이를 모사하기 위하여 해석모델의 경계에 상기 경계응력과 초기응력을 부여하고 역학적 평형해석을 실시하였으며 암석 균열을 따르는 응력과 변위를 살펴보았다.

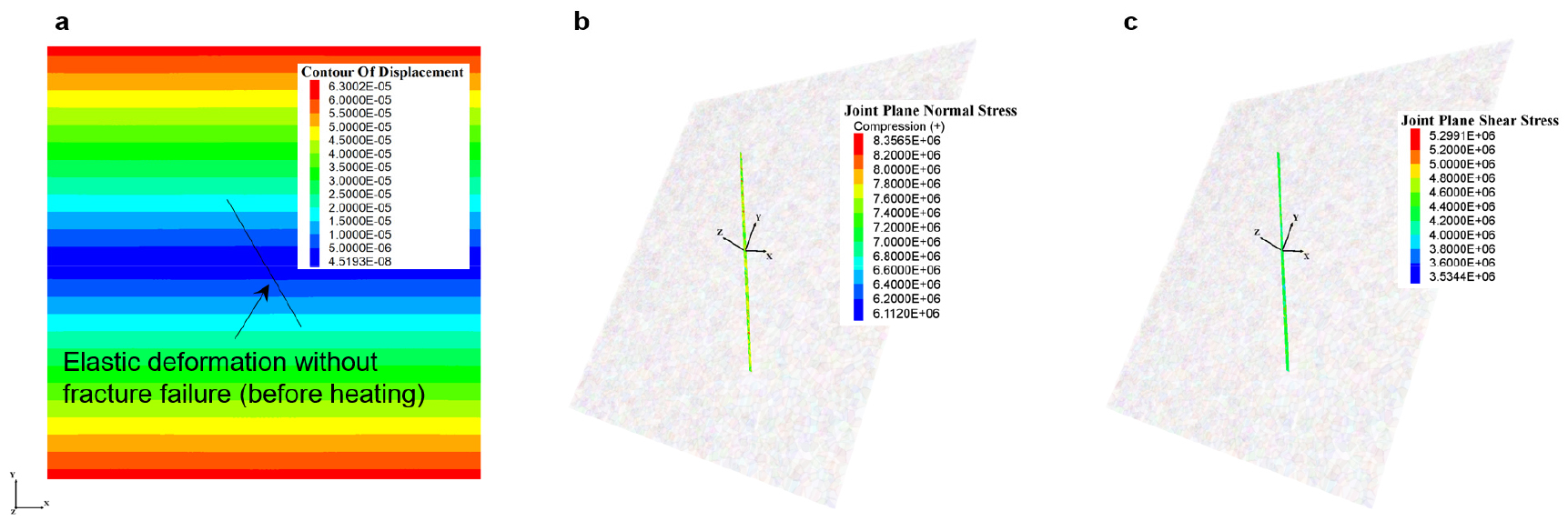
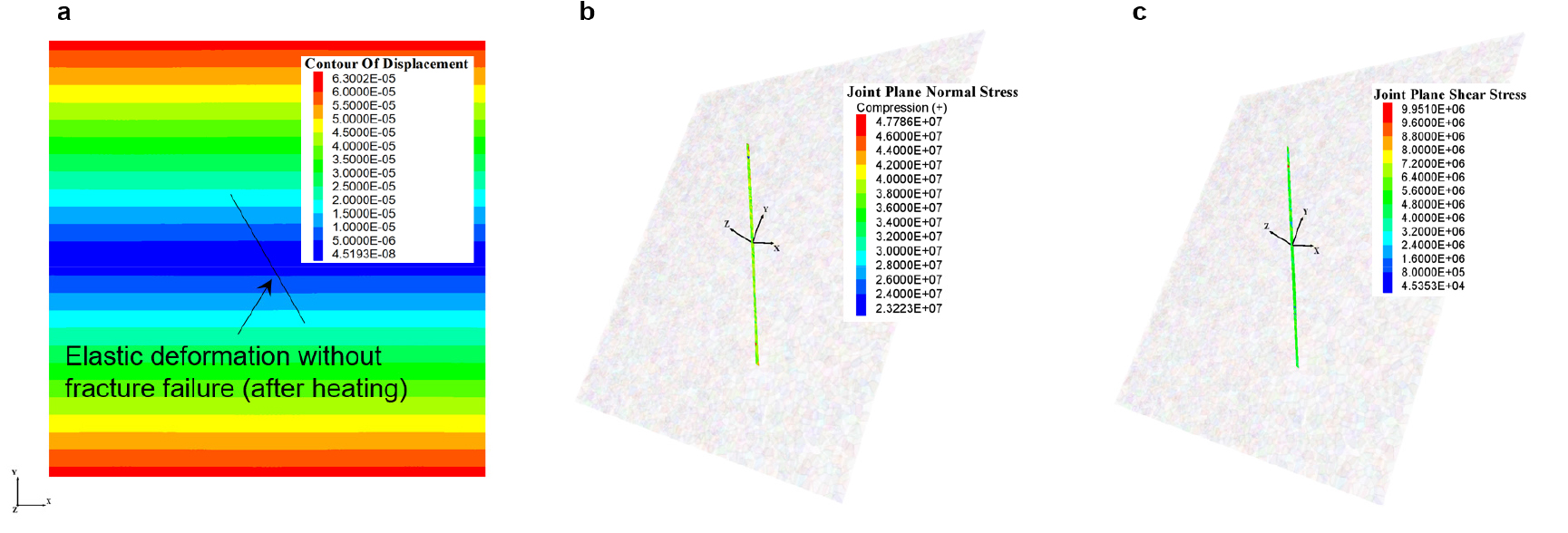
Fig. 4는 해석모델이 역학적 평형에 도달하였을 때 해석결과로서 전체 시료의 변위 분포와 함께, 균열면 상에 분포하는 contact 요소들의 수직응력과 전단응력을 보여주는 그림이다. 해석모델은 경계조건 하에서 평형에 이를 때까지 탄성거동을 보였으며, 균열을 따르는 파괴는 관찰되지 않았다. 최대주응력이 작용하는 y축 방향으로의 변위가 우세하게 발생하였고 암석균열이 변위 분포에 미치는 영향은 없었다. 이론적인 응력해석(Jaeger et al., 2007)에 따르면, 위 경계조건에서 60°의 경사를 갖는 면에 작용하는 수직응력(σn)과 전단응력(𝜏)은 각각 7.5 MPa, 4.3 MPa로 계산할 수 있다. 수치해석을 통해 얻어진 균열의 수직응력과 전단응력을 살펴보면, 일부 contact에서 다소 상이한 결과를 보였으나, 대체로 상기한 이론적 계산값과 유사한 범위 내에 분포함을 확인할 수 있었다.

Fig. 4.

Numerical result at completion of mechanical loading (before heating): (a) rock displacement magnitude, (b) fracture normal stress and (c) fracture shear stress magnitude

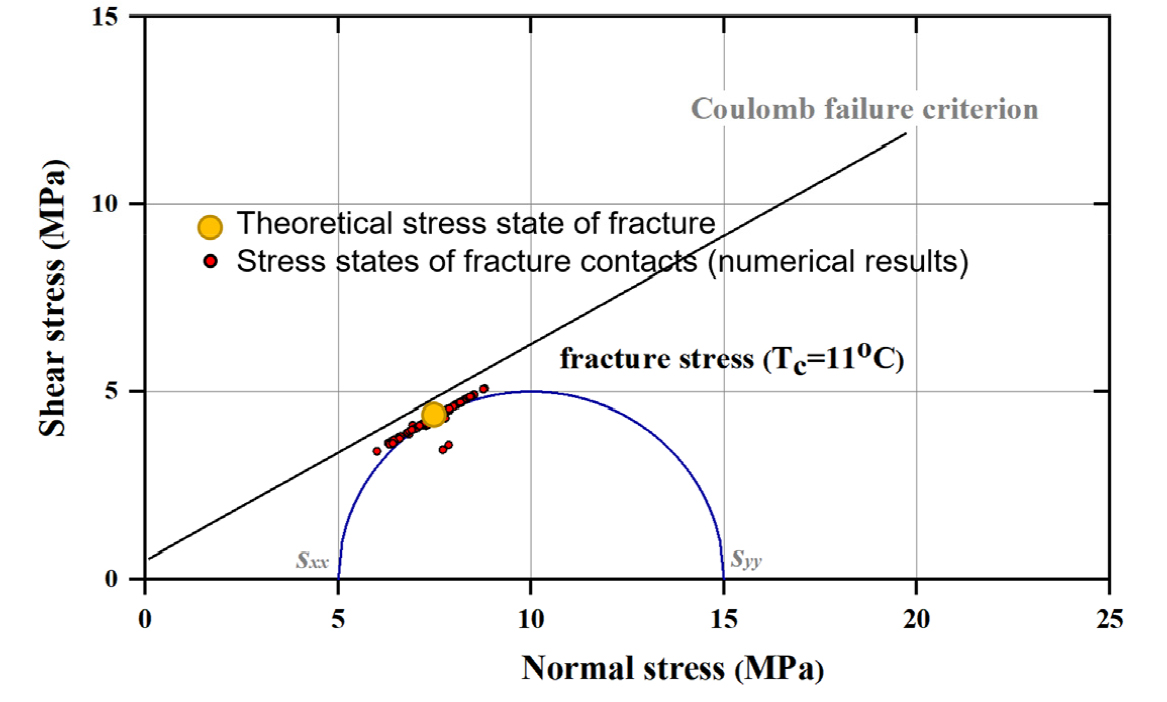
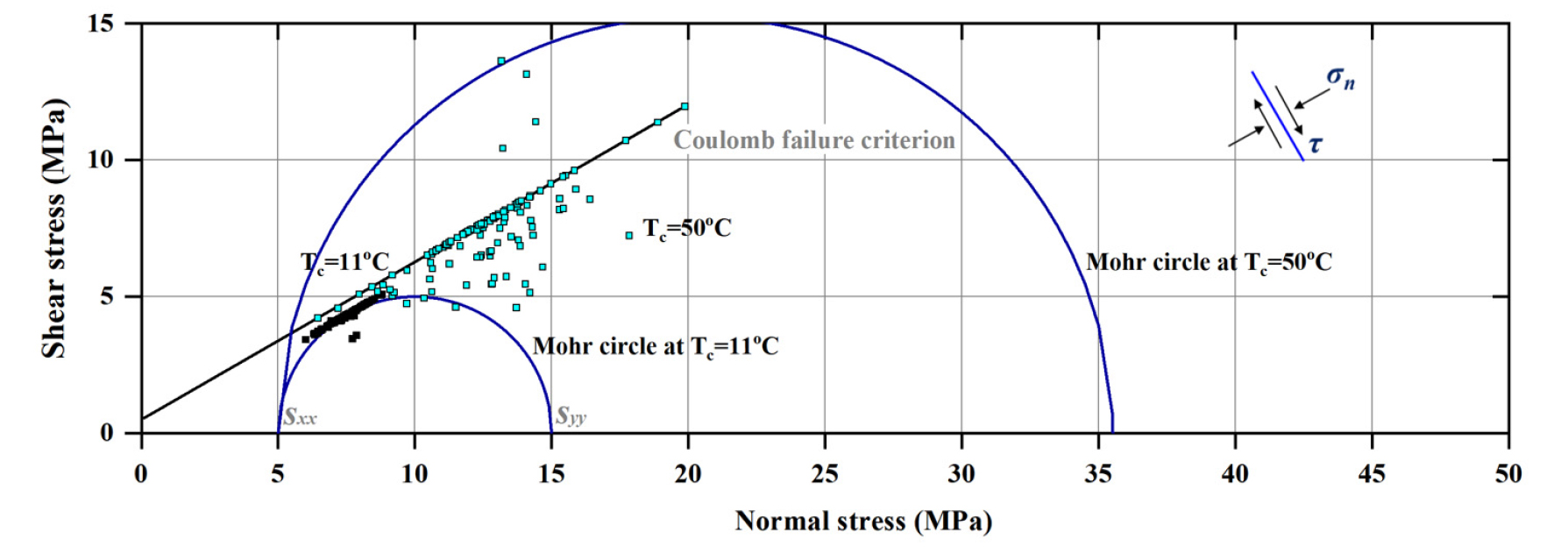
Fig. 5는 균열의 응력상태와 파괴포락선을 보여주며, Mohr 원을 통해 경계응력 상태를 함께 도시한 것이다. 경사가 60°인 균열의 응력상태는 이론적으로 Mohr 원 상에 노란색 원으로 표시할 수 있으며, 파괴포락선의 아래에 위치하는 것을 확인할 수 있다. 붉은색 원들은 수치해석 결과로서 역학적 평형해석 종료 시의 contact 응력 상태를 보여준다. 대부분 노란색 원 주위에 분포함을 확인할 수 있으며, 이론적인 예측치와 수치해석 결과 모두 역학적 하중 재하 시 균열의 전단파괴로 인한 미끄러짐이 발생하지 않음을 보여준다. Park et al.(2021)은 사면체 입자기반 개별요소모델 통해 이와 유사한 조건의 역학적 벤치마크 모델링을 수행한 바 있으며, 수치해석 결과와 이론식의 비교를 통하여 위 해석기법이 경계응력으로 인한 암석 균열의 전단거동을 합리적으로 재현함을 검증한 바 있다.

Fig. 5.

Theoretically and numerically calculated fracture stress states under the given boundary stress (before heating)

3.2 열전도에 의한 균열의 열-역학적 거동 – Case 1

벤치마크 모델의 열하중 재하(가열) 단계에서는 시료의 상부와 하부 경계면에 50°C의 일정 온도 조건을 설정하고, 시간의 흐름에 따른 열전도 해석을 수행하였다. 가열 과정에서는 열-역학 커플링 해석을 통해 블록의 열변형률 발생으로 인한 열응력의 증가를 계산하였으며, 시료 중심(균열 중심)의 온도(Tc)가 50°C에 도달하여 전체 시료가 완전히 가열되었을 때 해석을 종료하였다.

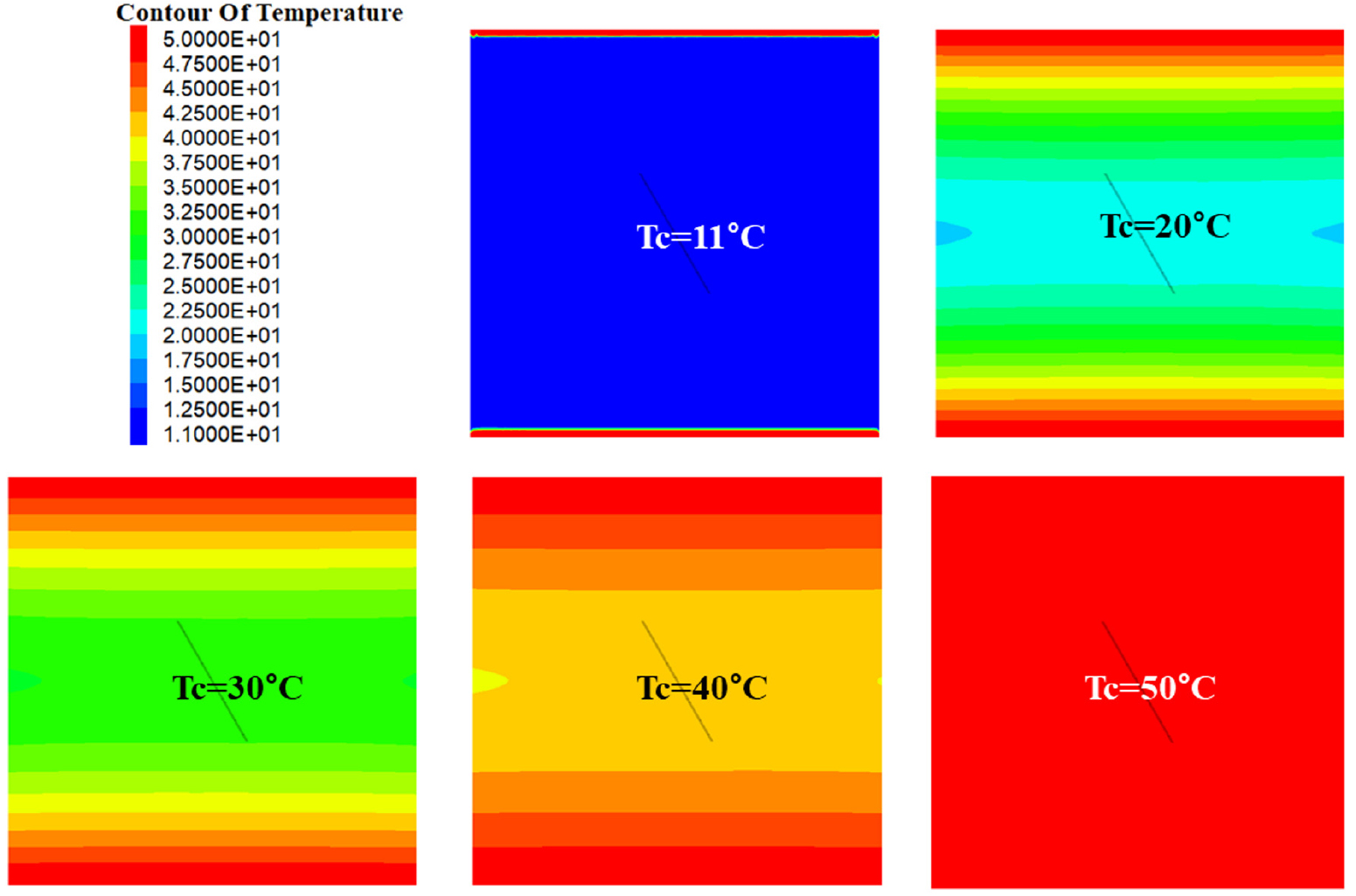
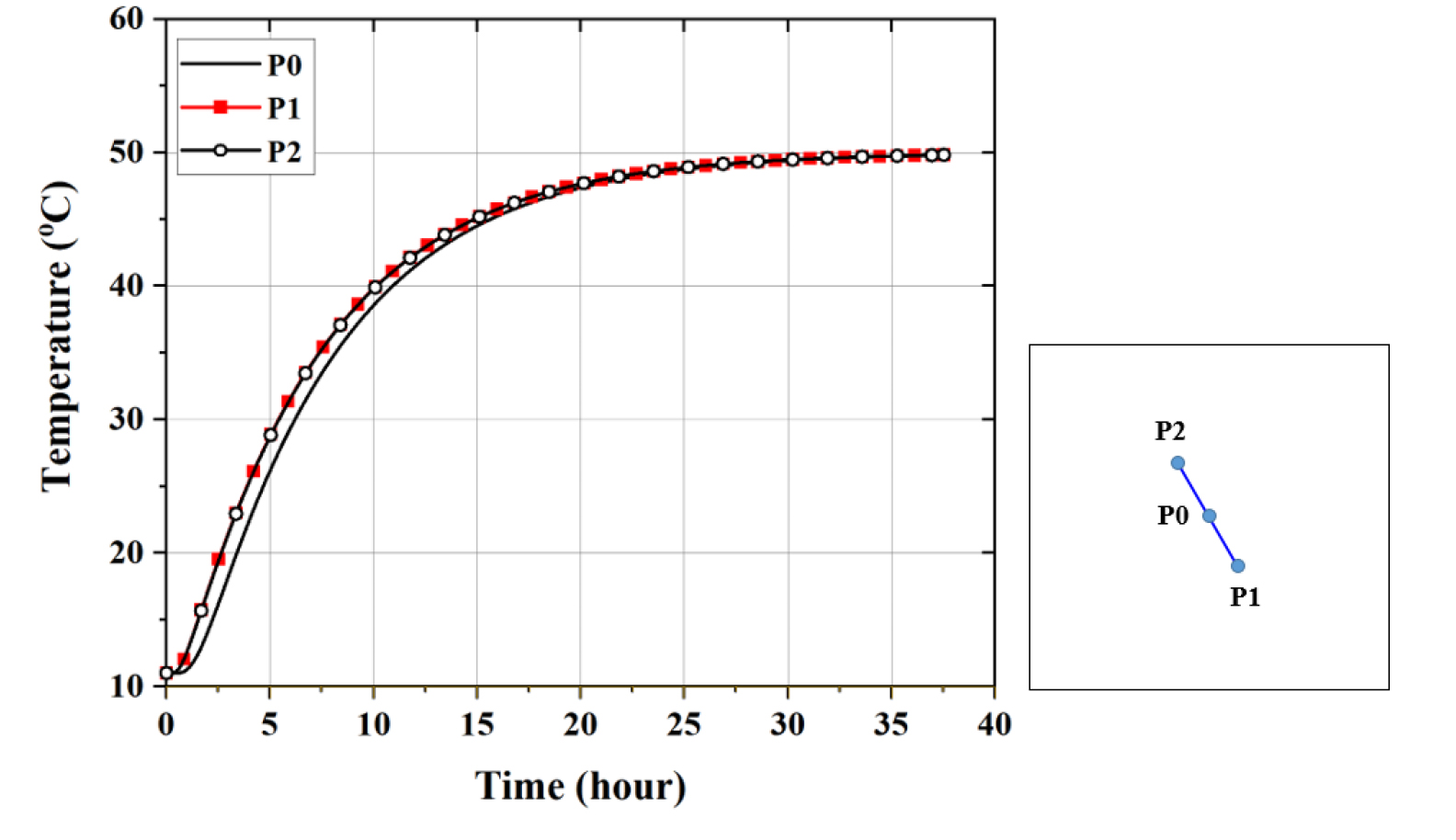
Fig. 6은 전도에 의한 열전달이 진행됨에 따른 해석모델의 온도분포를 보여주는 것으로 Tc가 11°C(초기상태), 20°C, 30°C, 40°C, 50°C(해석 종료)일 때의 해석결과이다. Fig. 7은 열전도가 진행되는 시간의 경과에 따른 균열 온도 변화를 나타낸 곡선으로, 모니터링 지점 P0, P1, P2는 각각 균열 중심과 양쪽 끝단을 의미한다. 수치해석에 따르면, 열전도에 의해 시료 전체가 50°C로 가열되는 데에 걸리는 시간은 약 37시간으로 나타났으며, 가열 초기의 온도 상승률이 높았고 시간이 경과함에 따라서 온도 상승률이 감소하는 결과를 보였다.

Fig. 6.

Contour plots of temperatures at Tc = 11°C, 20°C, 30°C, 40°C and 50°C

Fig. 7.

Fracture temperature change over time

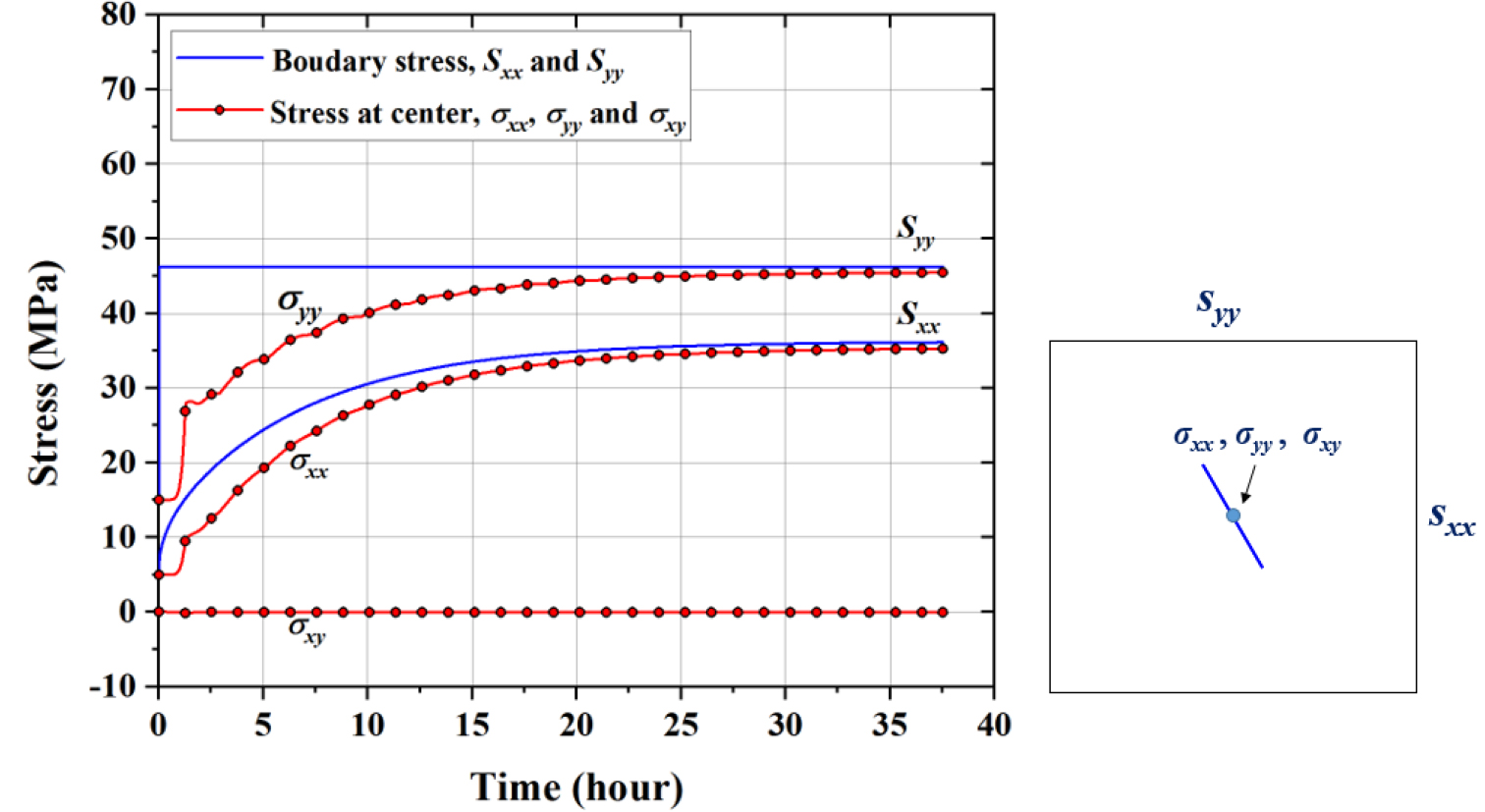
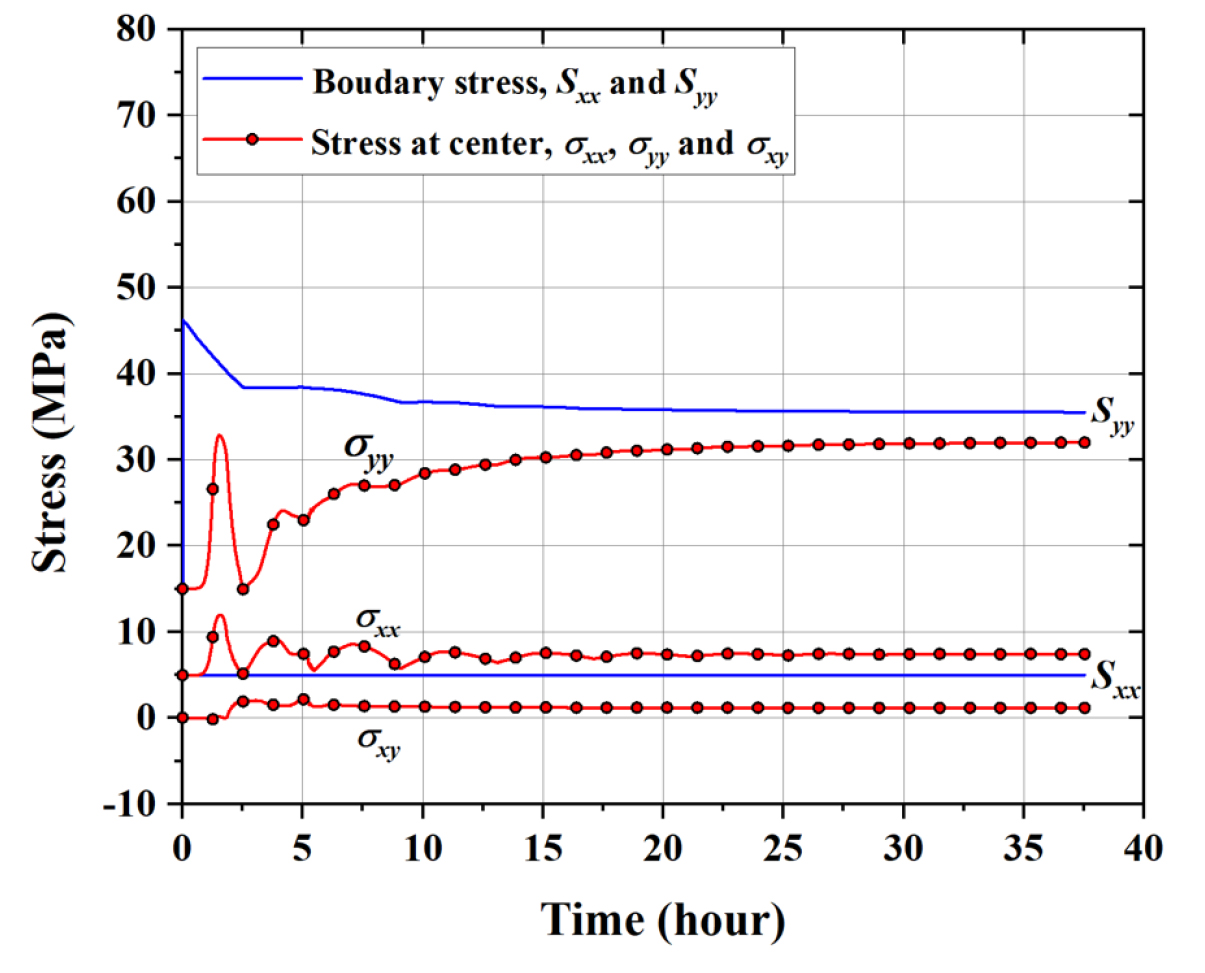
Fig. 8은 시간의 경과에 따른 경계응력과 시료 중심의 응력 변화를 보여주는 곡선으로, Sxx와 Syy는 수평, 수직방향 경계응력을, σxx,σyy,σxy는 각각 시료의 중심에 위치하는 zone 요소의 x, y 방향 법선응력과 xy 방향 전단응력을 의미한다. 수치모델에서 경계응력은 경계면에 법선방향으로 작용하는 총 힘(contact force)을 경계면 면적으로 나누어 계산한다. 수치해석모델에서는 상하부 경계면의 온도가 11°C에서 즉각적으로 50°C로 증가하는 것으로 모사되기 때문에 수초 내에 Syy가 15 MPa에서 약 46 MPa로 응력이 증가하는 것으로 계산되었다. 측면의 경우, 상하부와 가까운 부분에서는 온도가 50°C에 가깝지만, 중간부에서는 서서히 온도가 증가하므로 Sxx는 서서히 증가하게 된다. 해석 종료 시의 Sxx는 초기 5 MPa로부터 약 31 MPa 증가한 36 MPa로 계산되었다. 가열 단계에서는 추가적인 역학적 외력이 가해지지 않으므로 응력의 변화는 열팽창에 의한 응력 증가에 기인하며, Sxx와 Syy의 증가량은 거의 동일한 것으로 나타났다. 시료의 중심에서는 온도 증가에 따라 σxx와 σyy가 서서히 증가하는 경향을 보였고, 해석 종료 시에는 경계응력에 유사한 값으로 수렴하는 결과를 보였다. σxy의 경우에는 큰 변화를 보이지 않았는데, 이는 수치모델 상에서 열팽창과 열응력의 증가가 모든 방향으로 균일하게 발생하므로 최대, 최소주응력의 방향이 변화하지 않음을 의미한다.

Fig. 8.

Changes in boundary stress and rock stress at center over time

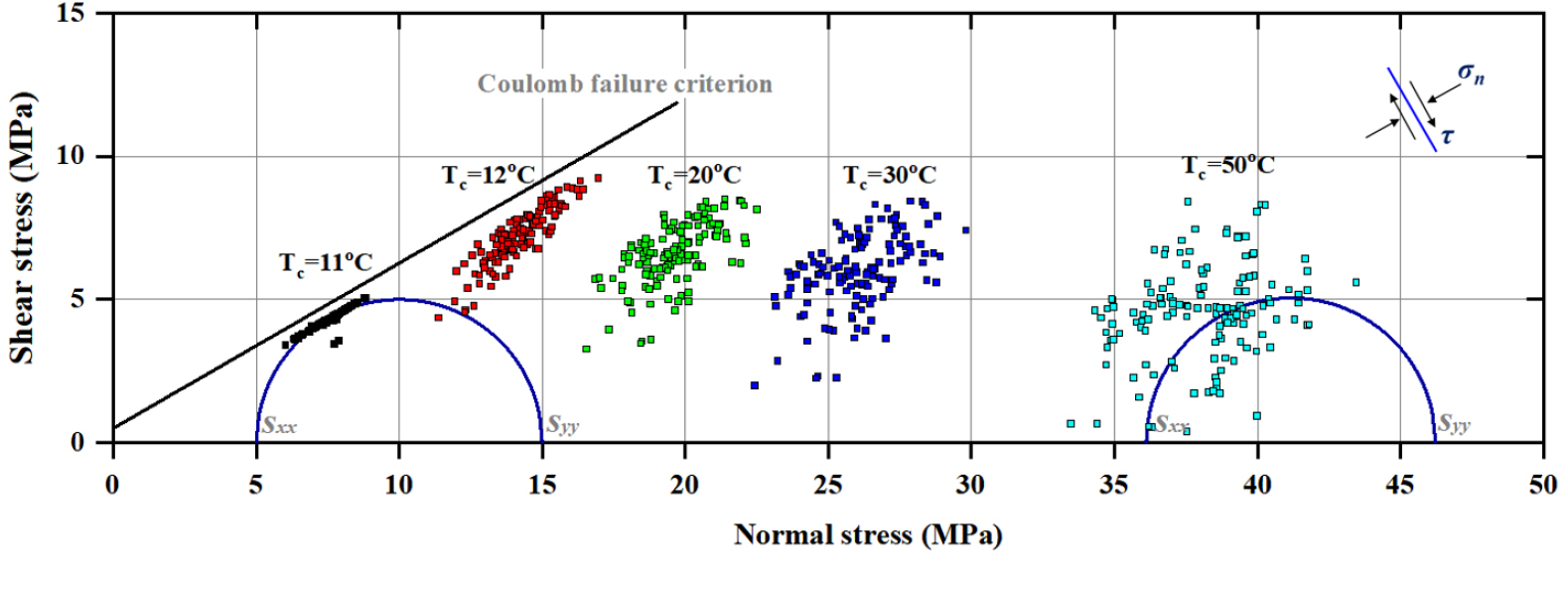
Fig. 9는 균열면 상에 분포하는 contact 요소들에서 구한 응력상태를 표시한 것으로 Tc가 11°C(초기상태), 12°C, 20°C, 30°C, 50°C(해석 종료)일 때의 해석결과이다. 여기에서는 Tc가 11°C일 때와 50°C일 때의 경계조건에 대한 Mohr 원과 균열의 파괴포락선을 함께 도시하였다. 해석 초기(Tc=12°C)에는 균열의 수직응력과 전단응력이 함께 증가하면서 파괴포락선에 근접하는 경향을 보였지만, 시간이 경과됨에 따라 수직응력의 증가가 두드러지고 전단응력의 변화는 크지 않았다. 균열을 따라 응력상태의 불균질성이 커지고 산포도가 증가하기는 하나, 가열이 진행됨에 따라 응력상태가 파괴포락선에서 멀어지는 것을 뚜렷이 관찰할 수 있었다. 경계응력에 대한 Mohr 원의 경우에도 반경을 유지한 채로 우측으로 이동하는 경향을 보였으며, 이는 가열이 진행됨에 따라 시료와 균열의 응력상태가 오히려 전단파괴에 대해 안정한 방향으로 변화함을 의미한다.

이러한 결과는 모든 법선방향으로의 변위를 구속한 경계조건에 기인한다. Fig. 8에서 살펴본 바와 같이, 온도가 증가함에 따라 시료 내부와 경계에서의 응력이 증가하기는 하나, 변위 구속조건으로 인해 모든 contact 요소에서 법선 방향으로의 열응력 증분이 동일하게 발생되며, 결과적으로 균열의 수직응력만이 증가하면서 전단강도가 오히려 증가하게 된다.

Fig. 9.

Changes in normal and shear stresses of fracture contacts with increasing temperature and Mohr’s circle presentation of boundary stresses at Tc= 11°C and 50°C

Fig. 10은 가열이 종료된 시점의 해석결과로서 전체 시료의 변위 분포와 균열면 상에 분포하는 contact 요소들의 수직응력과 전단응력을 보여주는 그림이다. 이를 Fig. 6의 해석 결과와 비교하여 살펴보면, 가열 전후의 변위 분포가 동일하며 균열 미끄러짐이 관찰되지 않는다. 균열의 수직응력은 크게 증가하였으며, 전단응력의 경우에는 국부적인 응력 집중에 의해 분산이 크게 나타나기는 하나 평균적으로 가열 전과 유사한 값을 보이는 것을 확인할 수 있다.

Fig. 10.

Numerical result at completion of thermal loading (after heating): (a) rock displacement magnitude (unit: m), (b) fracture normal stress (unit: Pa) and (c) fracture shear stress magnitude (unit: Pa)

3.3 열전도에 의한 균열의 열-역학적 거동 – Case 2

제3.2절에서 기술한 바와 같이, 열-역학적 벤치마크 모델에서 주어진 해석조건(Case 1)을 이용한 경우, 열에 의한 균열 미끄러짐 현상을 관찰할 수 없었다. 본 연구에서는 해석결과의 분석을 바탕으로, 그 원인이 가열단계에서 모든 방향의 변위를 구속한 경계조건 때문인 것으로 판단하였으며, 열에 의한 균열의 미끄러짐을 유도하기 위한 추가적인 경계조건(Case 2)을 제안하였다.

Fig. 11은 Case 2의 해석조건을 보여준다. 추가적으로 검토한 해석모델에서는 대부분의 해석조건이 전자와 동일하지만, 가열 단계에서 측면의 경계응력을 일정하게 유지한다. 즉, 가열 단계에서 상하부 경계면에서는 변위가 구속되지만 측면에서는 서보 컨트롤을 통해 5 MPa의 일정응력을 유지한다. 따라서 열전도에 의해 시료의 열응력이 증가하게 되면 측면의 경계부에서 변위가 발생하게 된다.

Fig. 11.

Boundary condition of thermo-mechanics benchmark model – Case 2

본 해석모델(3DEC)의 열-역학 커플링 해석에서는 역학적 변화가 열적 거동에 영향을 미치지 않는 것을 가정하므로, 온도 분포 해석결과는 Fig. 6과 Fig. 7에서 보인 Case 1의 결과와 동일하게 나타났다.

Fig. 12는 시간의 경과에 따른 경계응력과 시료 중심에서의 응력변화를 보여주는 곡선으로 용어에 대한 상세한 설명은 Fig. 8에서 기술한 바와 동일하다. 가열판이 설치된 상하부 경계면에서는 Case 1과 같이 해석 초기에 Syy가 15 MPa에서 46 MPa로 증가한다. 그러나 Case 2에서는 전자와는 달리 가열이 진행됨에 따라 응력이 감소하여 해석 종료 시 약 36 MPa에 수렴하는 것으로 나타났다. 측면 경계에서는 서보 컨트롤에 의해 x 방향 변위를 발생하면서 Sxx가 5 MPa로 유지되었다. 시료 내부의 온도가 증가하면서 시료 중심에서의 σxx와 σyy는 해석 초반 다소 변동을 보이며 증가하다가 해석 종료 시 31.5 MPa, 7.4 MPa로 수렴하였다. σxy의 경우, 큰 변화를 보이지 않았으나 약 2시간 경과 후 서서히 증가하기 시작하여 해석 종료 시 약 1.2 MPa의 값을 보였으며 이는 주응력 방향의 재배치가 발생하였음을 간접적으로 시사한다. 전반적인 변화 곡선을 살펴보면, 열전달에 의해 시료 내부에서 블록의 열팽창이 발생하게 되고 이에 따른 열응력이 증가하지만 수직방향과 수평방향의 구속조건이 상이하여 축차응력(differential stress)이 증가하고 있음을 확인할 수 있다. 또한, 서보컨트롤에 의해 수평방향으로의 열팽창이 허용되면서 수평방향뿐만 아니라 수직방향으로의 열응력이 완화되는 것(thermal stress release)을 관찰할 수 있었다.

Fig. 12.

Changes in boundary stress and rock stress at center over time – Case 2

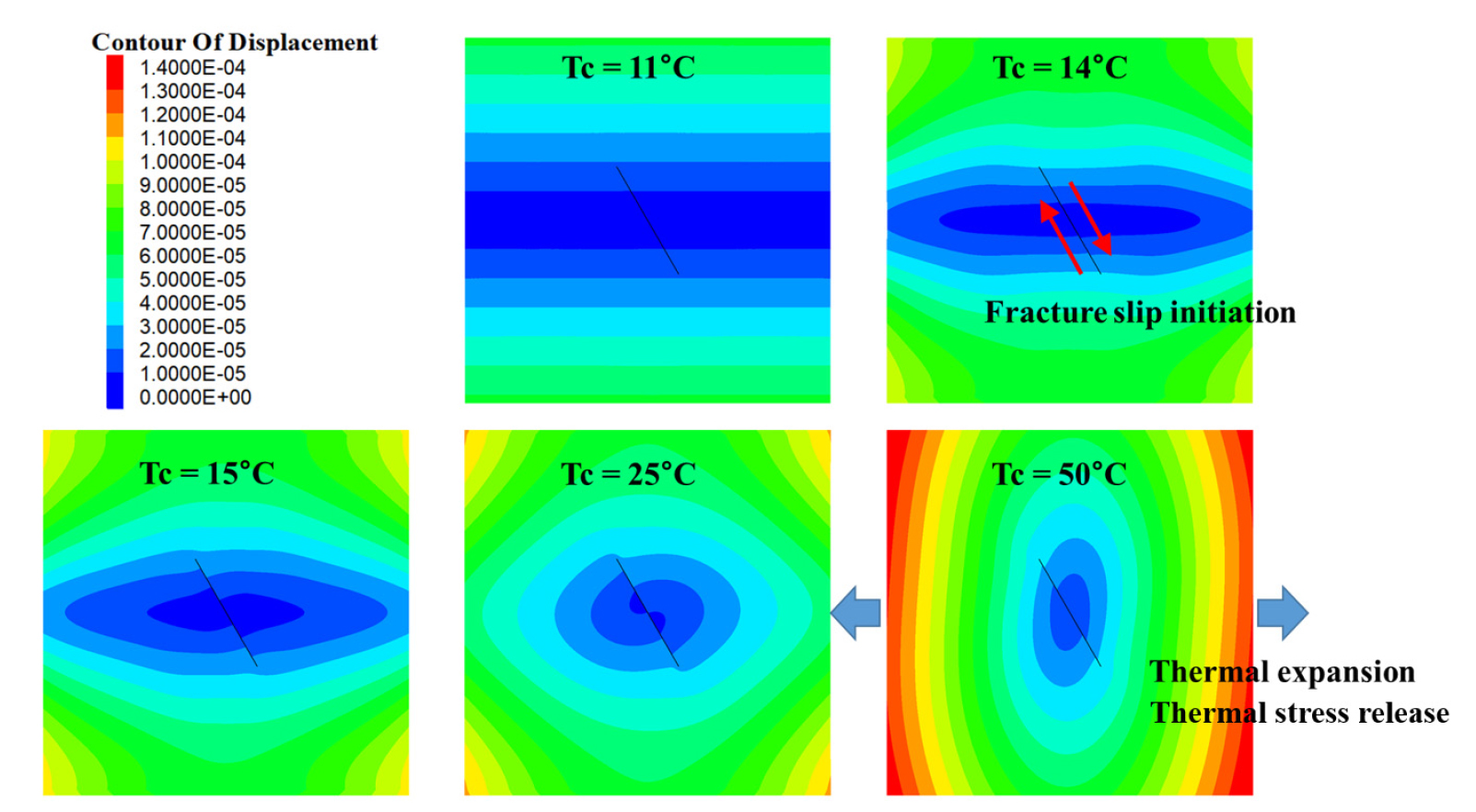
Fig. 13은 균열면 상에 존재하는 contact 요소들에서 구한 응력상태를 표시한 것으로 Tc가 11°C (초기상태) 50°C(해석 종료)일 때의 해석결과이다. 여기에서는 Tc가 11°C일 때와 50°C일 때의 경계조건에 대한 Mohr 원과 균열의 파괴포락선을 함께 도시하였다. Mohr 원의 비교를 통해 알 수 있듯이, 가열이 진행됨에 따라 축차응력이 증가하고, 가열 중 균열의 응력상태가 파괴포락선에 도달했음을 확인할 수 있다. Tc가 14°C일 때 균열의 전단파괴가 개시되어 미끄러짐이 발생하였으며 해석 종료 시 대부분의 contact 요소가 파괴 응력 상태에 이른 것으로 해석되었다.

Fig. 13.

Changes in normal and shear stresses of fracture contacts with increasing temperature and Mohr’s circle presentation of boundary stresses at Tc= 11°C and 50°C – Case 2

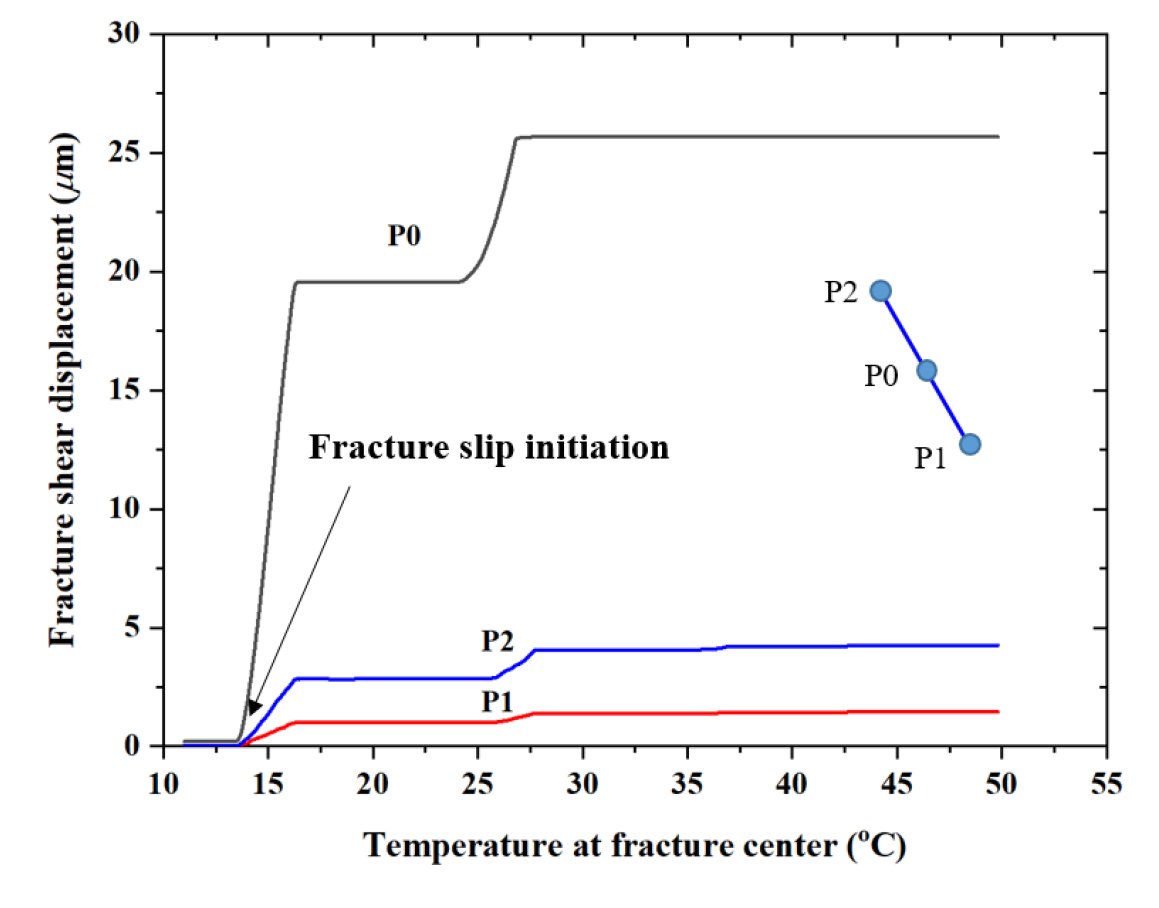
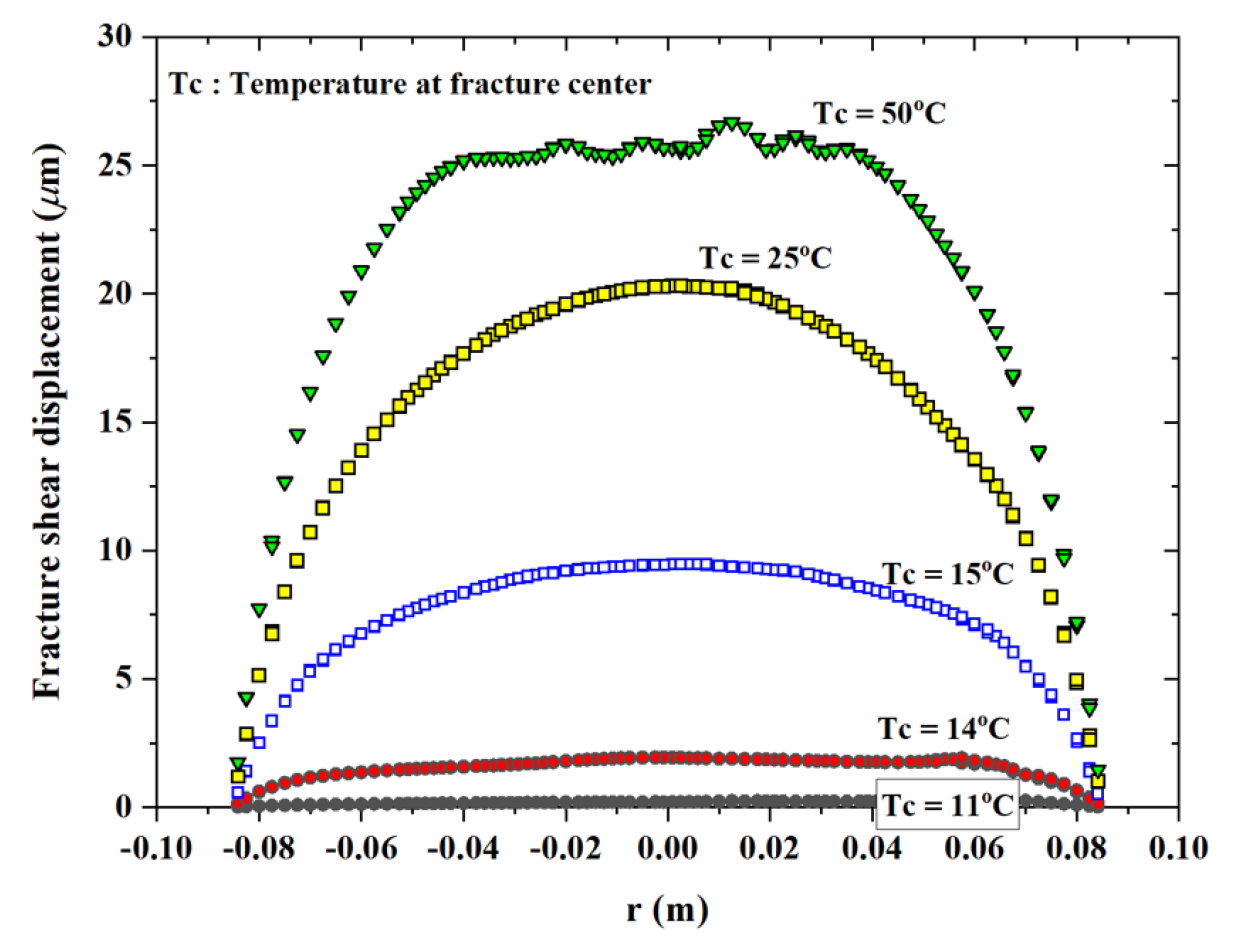
Fig. 14는 가열의 진행에 따른 암석의 변위 분포도이며, Fig. 15는 모니터링 지점(P0, P1, P2)에서 시간에 따른 균열의 전단변위를 보여준다. Fig. 15는 균열의 위치에 따른 전단변위 곡선을 보여주는 것으로 r은 균열 중심으로부터의 상대적 위치를 의미한다.

Fig. 14.

Contour plots of rock displacement magnitudes (unit: m) at Tc = 11°C, 20°C, 30°C, 40°C and 50°C

Fig. 15.

Change in fracture shear displacement with temperature

상기한 해석결과로부터 균열의 거동을 종합하여 살펴보면, 균열의 미끄러짐은 가열의 초기단계에 개시되는 것을 확인할 수 있다. 가열 전에는 상하부 경계면의 압축력에 의한 변위가 두드러지지만, 가열 후 Tc가 14°C에 이르면 균열 응력이 전단파괴 상태에 도달하면서 미끄러짐이 발생하기 시작한다. 대부분의 전단변위는 가열 초반에 발생하였으며, Tc가 27°C 이상일 때에는 추가적인 전단변위가 발생하지 않으며, 27°C 이상일 때 발생한 전단변위 곡선은 모두 Fig. 16의 50°C에 해당하는 곡선과 동일하다.

Fig. 16.

Fracture shear displacement vs. fracture position (r: position relative to fracture center)

4. 요약 및 결론

본 논문에서는 Voronoi 입자기반 개별요소모델을 통해 암석 균열의 열-역학적 연계거동을 모사할 수 있는 해석기법을 제시하고, 이를 DECOVALEX-2023 프로젝트 Task G의 벤치마크 연구에 적용한 해석결과를 소개하였다. 열-역학적 벤치마크 모델의 주요내용은 역학적, 열적 하중에 의한 암석 균열의 미끄러짐을 모사하는 것이다. 본 연구에서는 사면체 입자모델을 사용한 선행연구를 개선하여 Voronoi diagram을 생성하기 위한 일련의 프로세스를 제시하였다. 열-역학적 벤치마크 해석단계는 크게 두 단계로서 역학적 평형해석과 과도 열전도해석을 순차적으로 수행하여 경계응력의 재하와 가열이 암석과 균열의 응력 및 변위에 미치는 영향을 살펴보았다. 가열 단계에서는 변위구속 조건과 일정응력 조건의 두 가지 경계조건을 적용하여 균열의 미끄러짐이 발생하는 열-역학적 메커니즘을 고찰하였다. 변위구속 조건에서는 열팽창에 따른 열응력이 수평방향과 수직방향으로 거의 동일하게 증가하는 것으로 나타났다. 균열의 전단응력에는 큰 변화가 없었지만 수직응력은 온도 증가에 따라 선형적으로 증가하였다. 이에 따라 전단강도가 증가하였으며 전체 시료의 열전달이 종료된 시점에서도 균열 미끄러짐은 발생하지 않았다. 반면, 일정응력 조건에서는 수평방향으로의 열팽창으로 인해 열응력 완화 현상이 나타났고, 온도 증가와 함께 축차응력이 증가하여 균열면 전체에서 전단파괴가 뚜렷이 관찰되었다. 상기한 두 경계조건은 사실상, 현장의 경계조건을 매우 단순화한 모델로서 실제 암반조건은 두 경계조건 사이의 어딘가에 존재할 것이다. 위에서 살펴본 바와 같이, 열-역학적 연계거동 해석에서 경계조건이 해석결과에 결정적인 영향을 미치는 것을 고려할 때, 향후 현장 스케일의 해석모델 수립 시 열원의 위치나 현지응력 등을 현실적으로 반영한 경계조건 수립이 매우 중요할 것으로 판단된다.

본 연구에서 제시한 입자기반 개별요소모델은 암석 내 균열의 성장, 미시균열의 개시와 전파를 모사하는 데에 특장점을 가지고 있다. 상기 연구를 통해 제안된 Voronoi diagram 생성기법은 향후 균열 전파(fracture propagation)나 미세균열(mirco-cracking) 모델링 등에서 유용하게 활용될 수 있을 것으로 기대된다. 본 연구에서 제안된 해석기법은 DECOVALEX-2023 Task G를 통해 배포되는 실내실험 결과에 적용하여 그 타당성을 검증할 계획이다. 위 실험은 한국건설기술연구원에서 수행된 Thermo-Slip 실험(Sun et al., 2021)으로 화강암 암석절리면에 대하여 경계응력과 열응력(열원: 150°C)을 가하면서 절리면의 전단거동과 미소파괴음(acoustic emission, AE)을 측정한 연구이다.